40. Belgium and Luxembourg - temperature trends 1°C WARMING

In the next few posts I am going to take a look at the temperature trends in a few countries in western Europe, starting with Belgium. The unique feature of these countries is that they have some of the longest instrumental temperature records in the world.

Fig. 40.1: The temperature trend for Brussels since 1794. The best fit is applied to all the data and has a positive gradient of +0.67 ± 0.05 °C per century. The monthly temperature changes are defined relative to the 1976-2005 monthly averages.

 

The longest temperature record in Belgium comes, not surprisingly, from Brussels, and extends back to 1794 (see Fig. 40.1 above). That is the good news. The bad news is that there are no other temperature records with significant temperature data before 1973. Four records do have a couple of years of data in the early 1940s. But this data is probably not very reliable as there is then a thirty year gap to the rest of the data, and the early data was clearly collected under conditions of wartime occupation. The only other significant dataset comes from Luxembourg to the south of Belgium (see Fig. 40.2 below) which extends back to 1878.

The blue data in Fig. 40.1 above is the monthly temperature anomaly for Brussels, i.e. the amount by which each month's mean reading deviated from a reference value for that month for that station. Those monthly reference temperatures (MRT) were calculated by averaging all equivalent months (i.e. January or February etc.) in that dataset over the period 1976-2005. This is a later period than that used for most previous blog posts (most use 1961-1990) and is solely because of the lack of data before 1973. The monthly reference temperatures (MRT) are then subtracted from the raw monthly data to generate the monthly anomaly data. For a longer explanation of this process see Post 38 and Post 4.

It can be seen from the anomaly data in Fig. 40.1 that the range of anomaly values can be up to 12 °C, with the extreme negative values being more extreme than the extreme positive ones. These extreme negative values almost always correspond to severe winters; the winter of 1942 was particularly bad with two consecutive months (January and February) recording monthly means that were over 6 °C below normal. In the middle of a Nazi occupation I suspect that was really grim. Overall, though, this suggests that extreme winter cold spells are much deeper and longer lasting than prolonged summer heatwaves.

The other main feature of the data in Fig. 40.1 is the overall upward trend. Apart from a significant dip around 1890, this is almost continuous, and is illustrated more clearly by the 5-year moving average (yellow curve). Overall the mean temperature in Brussels rises by over 1 °C, as indicated by the red best fit line, from 1794 to 2013. However, as I pointed out in Post 14, the growth in energy usage in Belgium over the same period would be expected to raise temperatures by around 0.98 °C anyway. This would appear to indicate, that while the temperature rise is probably man-made, it is in all likelihood not entirely due to the emission of carbon dioxide and the Greenhouse Effect. 

It may be tempting to also discount this temperature record for Brussels as being an aberration or anomaly from the norm. However, if we compare it to the data for Luxembourg shown in Fig. 40.2 below, we see similar trends and features. There is a similar temperature rise after 1985, similar peaks in the 5-year moving average around 1947 and 1960, and a similar trough around 1890. The gradients of the best fit lines are similar in both cases as well, although the uncertainty for the Luxembourg best fit is much greater at almost ±0.16 °C. This, though, is partly due to the shorter time span of the Luxembourg data. 

Fig. 40.2: The temperature trend for Luxembourg since 1878. The best fit is applied to the interval 1895-2004 and has a positive gradient of +0.49 ± 0.16 °C per century. The monthly temperature changes are defined relative to the 1976-2005 monthly averages.

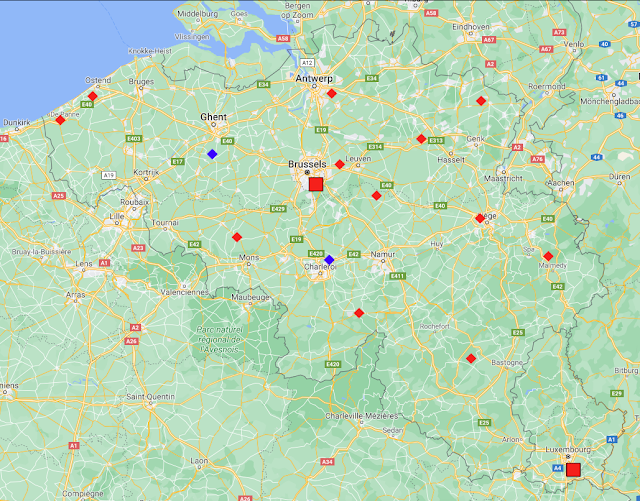
If we now look at the remaining data for Belgium and Luxembourg we see that there are an additional fourteen medium stations with temperature records that contain at least 480 months of data (see here for a list). Most of this data is for the period 1973-2013. The locations of the two long stations (Brussels and Luxembourg) and the fourteen medium stations are shown on the map in Fig. 40.3 below.

 

Fig. 40.3: The locations of long stations (large squares) and medium stations (small diamonds) in Belgium and Luxembourg. Those stations with a high warming trend are marked in red.

The map in Fig. 40.3 indicates that the two long stations with over 1200 months of data and the fourteen medium stations with over 480 months of data are distributed fairly evenly across Belgium and Luxembourg. This is important because it means that we probably don't need to resort to complex weighted averages when finding the overall temperature trend. A simple mean will suffice. In which case, combining the anomalies for the sixteen stations indicated in Fig. 40.3 gives the overall trend shown in Fig. 40.4 below.

Fig. 40.4: The temperature trend for Belgium and Luxembourg since 1794. The best fit is applied to the interval 1895-2004 and has a positive gradient of +0.52 ± 0.15 °C per century. The monthly temperature changes are defined relative to the 1976-2005 monthly averages.

 

As can be clearly seen, the overall trend for the whole of Belgium is not that different from that illustrated for Brussels in Fig. 40.1, but then why would it be? Over 80% of the trend in Fig. 40.4 is entirely due to the data from two stations: Brussels and Luxembourg. This is shown graphically in Fig. 40.5 below.

 

Fig. 40.5: The number of sets of station data included each month in the temperature trend for Belgium and Luxembourg.

 

Finally, if we compare these results using the raw data with those produced by Berkeley Earth which used adjusted data, we see broad similarities but some notable differences.

 

Fig. 40.6: Temperature trends for all long and medium stations in Belgium and Luxembourg since 1794 derived by aggregating and averaging the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1801-1980 and has a gradient of +0.28 ± 0.03 °C/century.
 

Combining the Berkeley Earth adjusted anomaly data for the same sixteen station records as in Fig. 40.4 and taking the mean value yields the two trends shown in Fig. 40.6 above: one trend for the 12-month average (in black) and a second for the 10-year average (in orange). For temperature data after 1860 the two trends are very similar to those published by Berkeley Earth and shown in Fig. 40.7 below, with the curves exhibiting similar patterns of peaks and troughs in the two figures. This does appear to validate our initial assumption that weighted averages are unnecessary when combining these temperature records due to their even geographical spacing. However, the Berkeley Earth data before 1860 looks slightly different, and quite frankly is unlikely to be very reliable, given that it is based on only one temperature record, or for the curve before 1794, on no local data at all. 

Fig. 40.7: The temperature trend for Belgium since 1760 according to Berkeley Earth.

Finally, if we look at the difference between the raw data shown in Fig. 40.4 and the Berkeley Earth adjusted data presented in Fig. 40.6 we see that while the overall net adjustments Berkeley Earth made to the data in this instance are small and result in a slightly negative contribution to the trend, there were still large corrections made to segments of the data before 1930 that in effect attempt to "flatten the curve". These do not appear to have a significant impact on the overall trend though.

Fig. 40.8: The contribution of Berkeley Earth (BE) adjustments to the anomaly data after smoothing with a 12-month moving average. The linear best fit to the data is for the period 1831-2010 (red line) and the gradient is -0.048 ± 0.009 °C per century. The orange curve represents the contribution made to the BE adjustment curve by breakpoint adjustments only.

Conclusions

It is clear from Fig. 40.4 that there has been a large degree of warming in Belgium and Luxembourg over the last 200 years. It is likely, given the agreement between the data from the two longest temperature records and their significant spatial separation, that this warming is a feature of the entire region, and is not localized to just one area (or maybe two) of the country, although given the lack of data before 1973, that is not a certainty. The magnitude of this warming is probably in excess of 1 °C. However, this temperature rise is only what one would expect from the growth of industrial energy use over this period (for Belgium it should be about 0.98 °C) as explained in Post 14. It is also less than the 1.5 °C we are told to expect for anthropogenic global warming (AGW) in the Northern Hemisphere as claimed by the IPCC and the HadCRUT4 data. Consequently, it does not really add support to the theory that carbon dioxide is the primary driver of warming, otherwise the warming should be much larger.

39. Namibia - temperature trends

When it comes to temperature data Namibia is not much better than Botswana. In total, there have only ever been 34 weather stations in Namibia (compared to 20 in Botswana). Of these only five are medium stations with more than 480 months of data, although nine have more than 450 months of data. This includes only two with more than 900 months of data and only four with any data before 1960. There is only one long station with over 1200 months of data (Windhoek), and only Walfisch Bay has any data before 1900. Unfortunately, both of these stations have portions of data that are clearly erroneous. The most likely explanation is that these data segments have either been incorrectly converted from Fahrenheit to Celsius when they were already in Celsius, or were not converted when they should have been.

 

Fig. 39.1: The temperature trend for Windhoek since 1911 according to Berkeley Earth (BE).

For the case of the Windhoek data, it is the data for the period 1911-1920 that is in question, as illustrated in Fig. 39.1 above. There is clearly an offset of more than 25 °C between the data before 1920 and the data after that date. What appears to have happened here is that some data that was correctly already in Celsius was assumed incorrectly to be in Fahrenheit. So when an unwanted correction of (x - 32)÷1.8 was applied to the data, the data was offset in a negative direction. Reversing this correction appears to remove the offset, as illustrated in Fig. 39.2 below.

Fig. 39.2: The temperature trend for Windhoek since 1911. The best fit is applied to the interval 1944-2001 and has a gradient of +2.21 ± 0.26 °C per century. The monthly temperature changes are defined relative to the 1971-1990 monthly averages.

The resulting temperature trend for Windhoek is strongly positive. However, the opposite is true for the only other significant temperature record that pre-dates 1920. This is the temperature record from Walfisch Bay, which is located at sea level on the coast about 200 km to the west of Windhoek (which is at altitude).

Fig. 39.3: The temperature trend for Walfisch Bay since 1885 according to Berkeley Earth (BE).

Like the Windhoek temperature record, the one for Walfisch Bay contains a significant amount of erroneous data (see Fig. 39.3 above). In this case, most of the questionable data have values that are forty degrees too large. This is almost certainly because these data values are recorded in Fahrenheit not Celsius. If we apply the appropriate correction, then the resulting data exhibits a strong negative trend as shown in Fig. 39.4 below. There are, however, ten data readings in Fig. 39.3 (from October 1941 to July 1942) where the offset is only about twenty degrees Celsius. The reason for this error is harder to ascertain and so these data points have been excluded from Fig. 39.4.

Fig. 39.4: The temperature trend for Walfisch Bay since 1885. The best fit is applied to all the data and has a negative gradient of -2.23 ± 0.16 °C per century. The monthly temperature changes are defined relative to the 1971-1990 monthly averages.

These are not the only station records with a significant amount of data before 1970, though. The graph below (Fig. 39.5) indicates that there are at least three other stations with such data. One is at J. G. H. Van Der Wath Airport (Berkeley Earth ID: 156958) which is at altitude near Keetmanshoop, while the other two are at Lüderitz (Berkeley Earth ID: 139074 and 156957) on the coast and about 200 km to the west of Keetmanshoop.

Fig. 39.5: The number of sets of station data included each month in the temperature trend for Namibia when the MRT interval is 1971-1990.

If we look at the data for J. G. H. Van Der Wath Airport (Berkeley Earth ID: 156958) we see that it exhibits a weak negative trend before 1980 of -0.43 ± 0.41 °C per century, but then shows a strong positive trend after 1980 of 3.3 ± 0.7 °C per century (see Fig. 39.6 below). Given the proximity of this station to both South Africa and Botswana, it is perhaps not surprising that the temperature trend resembles each of the trends seen in both those countries (see Fig. 37.2 and Fig. 38.1).

Fig. 39.6: The temperature trend for J. G. H. Van Der Wath Airport since 1933. The best fit is applied to the interval 1934-1978 and has a negative gradient of -0.43 ± 0.41 °C per century. The monthly temperature changes are defined relative to the 1971-1990 monthly averages.

The only other temperature data in Namibia from before 1970 comes from two stations at Lüderitz, a small coastal town (population: 12,500) in the south of the country on a similar latitude to Keetmanshoop. The two stations have different time frames that overlap between 1973 and 1986. The earliest data comes from Lüderitz Bay (Berkeley Earth ID: 156957) and extends from 1941 to 1986. The later data is for Lüderitz Diaz Point (Berkeley Earth ID: 139074) and extends from 1973 to 2013.

 

Fig. 39.7: The temperature trend for two stations in Lüderitz since 1941. The anomalies up to and including 1980 are for Lüderitz Bay (Berkeley Earth ID: 156957) while those from 1981 onwards are for Lüderitz Diaz Point (Berkeley Earth ID: 139074). The best fit is applied to the interval 1941-1995 and has a positive gradient of 0.27 ± 0.20 °C per century. The monthly temperature changes are defined relative to the 1971-1990 monthly averages.

 

If we combine the anomalies from the two Lüderitz stations we get the temperature trend shown above in Fig. 39.7. This has a very weak upward trend before 1990 which is followed by a sudden jump in temperature just before the year 2000. This temperature jump is similar in size to those seen after 1980 in data from Botswana (see Fig. 38.3), but it occurs about ten years later.  On the one hand this suggests that the temperature jump is a real phenomenon as it is seen in multiple station records, not just in Namibia, but also in Botswana, and to a lesser extent in South Africa. However, the variation in its timing across the different countries is a concern and means that we cannot completely trust its authenticity. What we cannot do is just ignore it.

Fig. 39.8: The temperature trend for Namibia since 1885. The best fit is applied to the interval 1944-2001 and has a positive gradient of +2.28 ± 0.17 °C per century. The monthly temperature changes are defined relative to the 1971-1990 monthly averages.

In addition to the five stations mentioned so far, there are another four stations with more than 450 months of data, as indicated in Fig. 39.5 above. Combining and averaging the anomalies from these nine stations yields the overall temperature trend shown in Fig. 39.8 above. This trend shares many features with those seen for Botswana (see Fig. 38.3) and South Africa (see Fig. 37.2). However, it also hints at the possibility of higher temperatures in the 19th century that would contradict the accepted conventional view of global warming in the 20th century. What is clear, though, is that once again there are significant differences between the actual raw data presented here and the temperature trend constructed by Berkeley Earth (see Fig. 39.9 below). The two most obvious differences are the temperature rises after 1980 and before 1920, both of which have been adjusted down by Berkeley Earth.

Fig. 39.9: The temperature trend for Namibia since 1860 according to Berkeley Earth.

Conclusions

The lack of high quality data makes definitive conclusions for the temperature trend in Namibia difficult. However, by comparing the Namibia data with that from neighbouring countries we can detect commonalities that allow some conclusions to be drawn.

1. For the majority of the 20th century little or no warming has occurred in Namibia, just as the same can be said for Botswana and South Africa.
2. There appears to have been a significant warming period after 1990. However, it is unclear what the cause of this is, and how long term it might be. It appears to be too abrupt and too large to be solely due to carbon dioxide.
   
3. There is weak evidence that 19th century temperatures in Namibia may have been much higher than those in the 20th century, just as we have seen previously in South America, Australia, New Zealand and the South Pacific. While the data before 1900 in each of these regions is scarce, the fact that there appears to be a consistent pattern across these regions for the temperature data that does exist would imply that the data is probably sound.
   

38. Botswana - temperature trends STABLE to 1980

Botswana illustrates some of the challenges in analysing temperature data in Africa. Simply, there just isn't enough data. In fact there is more temperature data for California than there is for the whole of Africa.

In total, there have only ever been twenty weather stations in Botswana. Of these only six are medium stations with more than 480 months of data. This includes only two with more than 900 months of data and only three with any data before 1960. There are no long stations with over 1200 months of data and there is no data before 1900. Moreover, as the map in Fig. 37.1 illustrates, those medium stations that do exist are not evenly distributed, but are instead concentrated along the South African border.

 

Fig. 38.1: The temperature trend for Botswana since 1917 based on an average of twelve stations records overall and only two before 1960. The best fit is applied to the interval 1917-1976 and has a negative gradient of -0.60 ± 0.29 °C per century. The monthly temperature changes are defined relative to the 1991-2010 monthly averages.

The lack of data also means that the overall temperature trend is very sensitive to the individual contributions from one or two atypical station records. This is highlighted in the difference between the trends shown in Fig. 38.1 above and Fig 38.3 below. 

The trend in Fig. 38.1 was constructed by the usual method of averaging the temperature anomalies from the various stations for each month from the earliest temperature observation (which for Botswana is January 1917) until the latest (October 2013). As I have explained before, the monthly anomaly is the change in the monthly temperature from a pre-defined reference temperature for that month and they are used so that temperature changes over time for different stations and different regions may be more easily compared. The mathematics of their calculation is explained here. However, there are a number of problems that arise when trying to calculate these monthly reference temperatures (MRTs).

The first thing to note is that the MRTs are different for each station record, and are also different for each of the twelve calendar months within each record in order to eliminate, or at least minimize, seasonal variations. The MRTs are usually determined by averaging a set of temperature readings from the same calendar month within that particular temperature record (although some climate science groups appear to corrupt this process by using a process of homogenization to combine data from adjacent stations). Ideally this averaging is done by choosing a time interval that is both reasonably long, and also one over which there is very little overall change in temperature. For these reasons a thirty year time interval of 1951 to 1980 would probably be best. It is long enough for the MRT values to be close to the true mean, and it appears that many temperature records around the world exhibit much less variation in temperature over this time period in comparison to both earlier and later time intervals. It is also the time interval that most of the climate science groups initially chose when highlighting climate change in the 1980s and 1990s.

Unfortunately, in many countries in the Southern Hemisphere there is much less temperature data before 1960 compared to that which was recorded post-1980. For that reason it is often better to choose a later time interval such as 1961-1990, or a shorter one of perhaps only twenty years, say 1981-2000.

The next problem, though, is that the temperature records in a particular region or country will not all be of the same length. More importantly, they usually have different amounts of data within the the MRT interval. The question here is, how many months of data do you need to average in order for the MRT to be sufficiently accurate? The higher the proportion needed, the more station records that will be excluded. Ideally we would want all stations to have 100% data coverage within the MRT time interval for all twelve months of the year. But equally, we would, ideally, also want all the station records to be included in the overall trend. In practice very few stations would meet the criterion of 100% data coverage so a lower threshold needs to be set. I generally choose between 40% and 60% with a higher threshold for a shorter MRT interval.

Ultimately the only way to determine the optimum method of determining the MRTs is to test different approaches. In the case of countries with a large amount of data, the different choices for the MRT time interval and the data coverage threshold have little overall impact. However, for countries like Botswana with small numbers of stations, these choices matter because the exclusion of one or two sets of station data can have a major impact on the final temperature trend. This is illustrated in the difference between the trend in Fig. 38.1 above and the one in Fig. 38.3 below. 

The temperature trend in Fig. 38.1 was constructed by first calculating the monthly reference temperatures (MRTs) for each station for the period 1991-2010. For this analysis only the fourteen stations with more than 180 months of data in total were included in the process (for a list see here). In addition, in order to optimize the accuracy in determining the MRT for each month for each station, only stations with data in more than 60% of months (i.e. 12 months) in the MRT period of 1991-2010 were included in the calculation. This resulted in twelve station records being included and two being excluded. The resulting number of station records incorporated in the trend for each month is shown below in Fig. 38.2.

Fig. 38.2: The number of sets of station data included each month in the temperature trend for Botswana when the MRT interval is 1991-2010.

Unfortunately, one of the stations that was excluded was Gaborone (Berkeley Earth ID: 152785), which is one of only three stations with any data before 1959. The other station excluded was Mahalapye (Berkeley Earth ID: 5699) which only has data from 1961 to 1990. The effect of including both these stations can be seen in Fig. 38.3 below. The effect is to change the temperature trend before 1976 from a negative trend of -0.60 °C per century to a positive one with a trend of +0.71 °C per century. This was achieved simply by changing the MRT interval to 1961-1990. While this resulted in the inclusion of the two stations at Gaborone and Mahalapye, it also meant that six stations with virtually no data before 1990 were excluded. This in turn has had a slight impact on the trend from 1990 onward, and in particular the magnitude of the cooling from 2002 onward.

Fig. 38.3: The temperature trend for Botswana since 1917 based on an average of three station records before 1960 but only eight in total. The best fit is applied to the interval 1917-1976 and has a positive gradient of +0.72 ± 0.26 °C per century. The monthly temperature changes are defined relative to the 1961-1990 monthly averages.

Conclusions

What the Botswana temperature data illustrates is the difficulty of deriving conclusive conclusions about climate change when there is insufficient data. The temperature trend before 1976 could be strongly positive (as shown in Fig. 38.3) or strongly negative (as shown in Fig. 38.1), depending on how representative the Gaborone data is of the country as a whole. Given previous evidence from Australia, Indonesia and South America regarding the disparity in temperature trends between large cities and the rest of the country, I would suggest that the Gaborone data is more likely to be an outlier even though Gaborone is hardly a megacity (its population is about 230,000). In which case it is more likely that the temperature trend in Botswana before 1976 would be very similar to that for South Africa (i.e. stable and flat) rather than the more or less continuous warming trend that has been claimed by groups such as Berkeley Earth (see Fig. 38.4 below).

Fig. 38.4: The temperature trend for Botswana since 1860 according to Berkeley Earth.

The other feature of note in both Fig. 38.1 and Fig. 38.3 is the large temperature rise from 1980 until 2002, followed by a smaller but significant decline. This temperature rise coincides with a much smaller one seen in the South Africa temperature data (see Fig. 37.2), but the warming in Botswana is about four times larger. It may be tempting to discount this warming as spurious or just bad data (as many climate scientists do when the data is not to their liking), but it features in too many different station temperature records to be ignored that easily. Instead it hints at the possibility of a more worrying phenomenon for climate scientists: namely that natural fluctuations in the regional temperature could be much larger and more persistent than they currently accept is possible.

37. South Africa - temperature trends STABLE to 1980

Over the next few posts I will look at the temperature data in Africa, starting with South Africa. Of all the countries in Africa south of the equator, South Africa has the most temperature data. However, the extent and quality of that data is still much less than that seen for even most individual states in Australia, let alone the entire country.

In total there are about 48 long and medium temperature records for South Africa with more than 480 months of data. Of these only five are long station records with more than 1200 months of data. The locations of these stations are shown below in Fig. 37.1 as well as the locations of similar stations in Namibia and Botswana. In South Africa the spread of the stations is fairly uniform. Sadly this is not true of Namibia and Botswana where the station densities are also much lower.

Fig. 37.1: The locations of long stations (large squares) and medium stations (small diamonds) in South Africa. Those stations with a high warming trend are marked in red.

If we average the anomaly data from the long and medium station records for South Africa we get the temperature trend shown below in Fig. 37.2. This has two main features. Before 1980 (when climate scientists first started claiming that global warming was happening) there is no warming at all. After 1980 there is a sharp rise of more than 0.7 °C. Details regarding how the anomalies in Fig. 37.2 were calculated have been outlined on previous blog posts, particularly Post 35 where the temperature trend for South America was calculated. This process involves calculating the mean reference temperatures (MRTs) for each of the twelve months of the year over a specific time interval (in this case 1961-1990) and subtracting them from the raw mean monthly temperatures to yield the anomalies.

Fig. 37.2: The temperature trend for South Africa since 1840. The best fit is applied to the interval 1857-1976 and has a gradient of +0.017 ± 0.056 °C per century. The monthly temperature changes are defined relative to the 1961-1990 monthly averages.

The number of stations in the average for each month in the temperature trend in Fig. 37.2 above is indicated in Fig. 37.3 below. As is clear from the graph, most of the station data was recorded between 1960 and 2000 with only one set of data continuing prior to 1880. Despite this, there is no evidence that the change in the number of stations over time has impacted the average temperature trend in Fig. 37.2 above in a manner that was seen for Indonesia (see Post 31). 

Fig. 37.3: The number of sets of station data included each month in the temperature trend for South Africa.

If we now compare these results with those published by Berkeley Earth we find similar patterns to those seen for data from other countries. Firstly, the average of the adjusted anomalies results in a temperature trend that is steadily increasing over time, not just after 1980, but also before (see Fig. 37.4 below).

Fig. 37.4: Temperature trends for all long and medium stations in South Africa since 1840 derived by aggregating and averaging the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1884-2003 and has a gradient of +0.87 ± 0.02 °C/century.

The data in Fig. 37.4 agrees remarkably well with that published by Berkeley Earth and shown below in Fig. 37.5, even though I have only used stations with more than 480 months of data, and have not weighted any of the those stations differently when computing the average. This demonstrates that the fairly even geographical spread of the stations across South Africa eliminates the need to apply different weightings to each dataset. It therefore also justifies the use of the same simple averaging process for calculating the temperature trend in Fig. 37.2.

Fig. 37.5: The temperature trend for South Africa since 1850 according to Berkeley Earth.

The outstanding question is why does the data published by Berkeley Earth in Fig. 37.5 differ so markedly from that for the real anomaly data in Fig. 37.2. The answer is of course once again down to the use of breakpoint adjustments and homogenization by Berkeley Earth. The sum total of these contributions have been calculated and are shown in Fig. 37.6 below. They clearly show that large upward adjustments were made to most of the temperature data around 1890-1900 and 1930-1940.

Fig. 37.6: The contribution of Berkeley Earth (BE) adjustments to the anomaly data after smoothing with a 12-month moving average. The linear best fit to the data is for the period 1881-2000 (red line) and the gradient is +0.59 ± 0.03 °C per century. The orange curve represents the contribution made to the BE adjustment curve by breakpoint adjustments only.

Conclusions

1) There is no evidence of any warming of the climate in South Africa before 1980 according to the raw temperature data.

2) There appears to be a sudden sharp rise in temperature after 1980 that is not consistent with the gradual increase in CO₂ levels seen since 1850. 

3) Once again the temperature trend constructed by Berkeley Earth appears to be strongly affected by their own data adjustments via breakpoints and homogenization.

 

36. Lateral thought #2 - does human respiration cause carbon dioxide levels in the atmosphere to increase?

Does breathing contribute to a build-up of carbon dioxide in the atmosphere? This was the subject of an article on the Skeptical Science website that I came across recently that claimed to be debunking a climate myth. That supposed myth was that breathing contributes to a build-up of CO₂ in the atmosphere.

The article is not new: it was first published ten years ago. The central point of the article was to refute claims supposedly made by climate sceptics that breathing by humans adds carbon dioxide to the atmosphere, and so contributes to global warming. But after reading the article and many of the comments I realized that not only was the entire article wrong, so too were most of the comments. 

The motivation for the article appears to be a throw-away comment by Australian academic Professor Ian Plimer, Professor of Mining Geology (University of Adelaide) and Emeritus Professor of Earth Sciences (University of Melbourne), in an ABC radio interview regarding his latest book. The comment was a response to claims made in a green paper by Australian Climate Minister and Senator Penny Wong regarding the threat of climate change where she claimed carbon was a pollutant. In reply Professor Plimer said:

"If Senator Wong was really serious about her science she would stop breathing because you inhale air that's got 385 parts per million carbon dioxide in it and you exhale air with about ten times as much, and that extra carbon comes from what you eat."

I'm still not sure why that statement riled the people at Skeptical Science so much, other than it came from a climate sceptic attacking a supporter of global warming. To me it just seems like a statement of fact and a reference to the carbon cycle. It is therefore doubly puzzling that those same people at Skeptical Science then chose to use the carbon cycle to refute a claim that was not explicitly made, namely that breathing contributes to a build-up of CO₂ in the atmosphere. The argument outlined in the rebuttal by Skeptical Science basically came down to saying:

"Therefore, when we breathe out, all the carbon dioxide we exhale has already been accounted for. We are simply returning to the air the same carbon that was there to begin with."

The problem is this is not quite true. Actually, it is not true at all. In fact I will now explain why breathing by humans may have actually contributed to a build-up of CO₂ in the atmosphere over the last 100 years.

 Fig. 36.1 The carbon cycle.

The first problem with invoking the carbon cycle is that there is no such thing. There is no single carbon cycle. Instead there are multiple interlocking cycles as illustrated in Fig. 36.1 above. I've listed three possibilities below.

Atmosphere  ==>  plants  ==>  soil (bacteria)  ==>  atmosphere.

Atmosphere  ==>  plants  ==>  animals  ==>  atmosphere.

Atmosphere  ==>  ocean plants (algae)  ==>  oceans (bacteria)  ==>  atmosphere.

So the CO₂ doesn't just go round in a circle, as is claimed: it goes around multiple circles. 

The second problem is that the carbon cycle only describes the steady state. So you can’t use it to prove that human respiration isn’t increasing CO₂ levels in the atmosphere because the human population has grown exponentially over the last 100 years. It has almost quadrupled since 1920. That is not a system operating in the steady state or at long-term equilibrium.

In essence, the carbon cycle describes five competing carbon reservoirs or sinks (vegetation, animals, soil, the ocean and the atmosphere) all of which also act as carbon pumps. Moreover, these five reservoirs are all interconnected, and the pumping capacity of each depends on their size. Generally, the bigger they are, the more carbon they will pump. That interconnection means that changing the size of one will change the size of all the others in order to a) balance the pumping rates, and b) to ensure that the law of conservation of mass, as applied to the amount of carbon in the system, is never violated. These changes will happen as the system seeks to find a new equilibrium position or steady state. 

So in principle, any change to either the pumping rate or the size of a reservoir will have knock-on effects throughout the rest of the carbon cycle. That means that any increase in the human population will affect everything else. We can, however, estimate what some of these changes might be based on what we know about the change in human population over the last 100 years.

As the average 70 kg person generates about 1 kg of CO₂ per day, that means they transfer 100 kg of carbon to the atmosphere every year. This carbon comes from the food they eat. With nearly 8 billion people on the planet that equates to about 0.8 GtC per annum (GtC = gigatonne of carbon) being transferred into the atmosphere.

But that is not all. The average person probably eats their own bodyweight in meat every year. So the growth in the human population since 1920 must be reflected in a similar percentage growth in the number of farm livestock. If we assume there is about 2 kg of livestock per 1 kg of human (i.e. a 2 year supply of meat in production), then the overall CO₂ production from both will be about 2.4 GtC per annum. This is about a quarter of our fossil fuel CO₂ output so it is not insignificant. But is this directly increasing atmospheric CO₂ levels as some climate change deniers might claim (although I'm not entirely sure which)?

Some people have suggested that the increases in human and livestock CO₂ emissions are offset by increased crop production. Their argument is that, as all the carbon we breathe out comes from crops, any increase in the CO₂ produced by the human population will be offset by a commensurate increase in crop production required to feed the extra humans and their livestock. That in essence is the core of the original rebuttal from Skeptical Science outlined above. The problem is that this is not true either.

Increased crop production comes at the expense of other types of vegetation (e.g. forests). The total area under human cultivation may increase, but the total amount of land and vegetation won’t. All available fertile land is already fully occupied with vegetation, so any increase in farmland will be at the expense of wild countryside. Changing usage from one to the other does not increase CO₂ uptake because both types of land are already doing this. For example, deforestation in the Amazon region driven by the desire to grow crops and farm cattle does not increase the rate of CO₂ capture in the region. If anything, it decreases it. Forests, so we are told, are the best carbon dioxide scrubbers.

Also, increasing the number of animals does not increase the amount of vegetation or its growth rate. Instead it decreases the amount of carbon going into the soil. Animals eat plants before those plant can die and before they can decay in the soil. This means that animals replace the CO₂ producing capacity of the soil. That is where the substitution occurs. And if the pumping efficiencies of both animals and the soil were the same then nothing much would change as the animal population increases. But they aren’t the same. 

The carbon pumping efficiency of the soil is only 4%. As Fig. 36.1 indicates, the soil contains 1580 GtC globally but emits 60 GtC per annum. Humans store only 0.1 GtC but emit 0.8 GtC per annum. That is an efficiency of 800%. If we include livestock, the efficiency will be broadly the same (800%) but the size of the carbon reservoir and CO₂ emissions will both be about three times greater, for the reasons outlined above. This also means that the increase in CO₂ production from humans and livestock is the same as that produced by about 4% of the Earth’s soil. The consequence of this is that the volume of the soil must reduce by 4% over time as its pumping capacity is replaced by human and their animals, and the amount of carbon entering it from dead plants declines. 

So 63.2 GtC will be lost from the soil while only 0.3 GtC will be transferred to storage in humans and animals, and none to plants. There is only one other place that most of the 62.9 GtC can go: the atmosphere. This 62.9 GtC will increase the atmospheric CO₂ concentration by about 25-30 ppm. So the human population increase could have increased atmospheric CO₂ levels by up to 30 ppm over time, and about 20 ppm since 1920.

Fig. 36.2: A schematic illustration of the carbon cycle on land.

 

To understand this more fully consider the schematic diagram in Fig. 36.2 above. This represents the part of the carbon cycle involving exchange of carbon between the air and land in the case where initially there are no animals in existence. The terms T₁-T₄ are the flow rates of carbon between the three reservoirs, with the size of each reservoir indicated in parentheses. The four flow rates represent carbon capture in plants by photosynthesis (T₁), respiration from plants and animals (T₂), the transfer of dead plant and animal matter to the soil (T₃), and the decay of organic matter in the soil to release CO₂ back into the atmosphere (T₄).

In equilibrium the flow rates into and out of each reservoir must balance. So 

T₁ = T₂ + T₄

(36.1)

 

T₁ = T₂ + T₃

(36.2)

and

T₃ = T₄

(36.3)

Only two of these equations are independent. In addition, the total amount of carbon in the system must remain constant at 2940 GtC (=1580+610+750).

Now suppose the ecosystem outlined in Fig. 36.2 initially contains only plants and bacteria in the soil. Then we introduce some animals. The effect of animals is to eat some of the plants and emit CO₂. This means respiration (T₂) must increase by an amount x and the amount of plant matter entering the soil (T₃) must decrease by the same amount in order for Eq. 36.2 to balance. For the case of the addition of humans and livestock we have already estimated that x = 2.4 GtC per annum. 

The problem is that both Eq. 36.1 and Eq. 36.3 now no longer balance. Only Eq. 36.2 remains balanced. So the soil will lose 2.4 GtC per annum and the atmosphere will gain 2.4 GtC per annum. There is a mass transfer of carbon from the soil to the atmosphere. This will only stop when the emission of CO₂ from the soil (T₄) decreases, as it will do gradually due to the slow and gradual reduction in its volume. When that happens both Eq. 36.1 and Eq. 36.3 will once more balance and the mass transfer will stop. That will happen when T₄ has also decreased by x. As T₄ was initially about 60 GtC per annum, this requires a 4% reduction in T₄, and therefore a 4% reduction in the volume of the soil, i.e. 63 GtC (the rate of decay of the soil and its rate of emission of CO₂ must be proportional to the soil volume). That amounts to a total mass transfer of approximately 63 GtC to the atmosphere, the same as in our preliminary calculation above.

Is this an upper estimate? Yes, probably. It assumes that the growth in the human population and farming livestock is a net gain in terms of animal numbers and that they do not merely substitute for the loss of other species. But we know this is not true. Humans and their livestock do displace other creatures to some extent. This analysis also omits any additional loss of CO₂ to the oceans and changes to vegetation volumes through loss of soil (down 4%) and increasing growth rates due to increased CO₂ levels in the atmosphere (up by 8%). But what it does demonstrate is that when the human population changes, everything else changes. 

 

Conclusion

What we have shown here is that changes to the ecological balance between plants and animals changes the concentration of CO2 in the atmosphere. So respiration by humans and other animals can contribute to a build-up of carbon dioxide in the atmosphere.

35. South America - temperature trends 0.5°C WARMING

The land area of South America is more than twice that of Australia while its population is more than sixteen times greater. Yet it has fewer high quality temperature records than New South Wales.

Overall South America has about 1000 temperature records, but only 21 have more than 100 years, or 1200 months, of data. Of these long station records, the longest is that of Rio de Janeiro (Berkeley Earth ID: 152852). Its earliest temperature data dates from 1832 and clearly shows that temperatures in the city at that time were higher than today (see Fig. 35.1 below). The average temperature then declined throughout the 19th century before recovering over the last 100 years. This behaviour is not unique to South America. We have seen it in both Australia and New Zealand previously, and if other countries in the Southern Hemisphere had longer records, we might have seen it in many other places as well. 

 

Fig. 35.1: The temperature trend for Rio de Janeiro since 1832. The best fit is applied to the interval 1921-1990 and has a gradient of +2.06 ± 0.15 °C per century. The monthly temperature changes are defined relative to the 1951-2000 monthly averages.

However, the extent to which the Rio data reflects the overall temperature trend in South America is harder to determine. Of the 1000 or so sets of station data from South America, only about 318 have more than 40 years, or 480 months, of data, and as I have shown in previous posts, even this length of data is insufficient to ascertain the recent overall temperature trend, let alone its longer term context. 

The approximate locations of the long and medium stations in South America are shown on the map below. It can be seen that they are fairly evenly spread throughout the continent, but with the Amazon region, not surprisingly, being less well represented. 

Fig. 35.2: The locations of long stations (large squares) and medium stations (small diamonds) in South America. Those stations with a high warming trend are marked in red.

In order to determine the overall temperature trend for South America we need to average the temperature anomalies from all the different stations in the region, as I explained in Post 5. These temperature anomalies are not the actual average monthly temperatures for each location, but the amount by which those average monthly temperatures change relative to a defined reference value for that month. That monthly reference temperature (or MRT), is usually an average of the values for that month over a given period, say 1961-1990. However, as I have pointed out in many previous posts, the way anomaly data used by climate groups like Berkeley Earth is calculated is not quite that straightforward. 

The anomaly data used by climate groups is also subject to adjustments via processes such as homogenization and breakpoint alignment. In homogenization, neighbouring sets of station data are compared and averaged to determine the monthly reference temperature values (MRT) for the target station. Once this homogenized MRT is subtracted from the monthly temperature to yield the anomaly for that month, a number of breakpoint adjustments are then made to different segments of the anomaly data in that dataset, supposedly to correct for bad data and other behaviours seen in the data that appear to be incongruous. The problem with both these interventions is that they are not neutral. Analysis from almost all the previous data I have examined so far in this blog has shown that both these interventions tend to add significant warming to the temperature trends after 1900. The data presented here for South America is no exception.

It is relatively easy to calculate the magnitude of the adjustments made by Berkeley Earth, because conveniently Berkeley Earth list both the adjusted and unadjusted anomaly data in each data file, together with the original raw temperature data. If we average the Berkeley Earth adjusted anomaly data from all the long and medium stations identified in Fig. 35.2 above, the result is the curves shown below in Fig. 35.3.

Fig. 35.3: Temperature trends for all long and medium stations in South America since 1832 derived by aggregating and averaging the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1900-1999 and has a gradient of +0.85 ± 0.02 °C/century.

The temperature trends shown in Fig. 35.3 above clearly exhibit a strong warming of more than 1.0 °C after 1890. The other notable point is how well the data in Fig. 35.3 agrees with the official Berkeley Earth version shown in Fig. 35.4 below. This can be verified by comparing the pattern of peaks in the 12-month moving average in each case. This shows that using different weightings for each set of station data when calculating the average is not needed.

Fig. 35.4: The temperature trend for South America since 1850 according to Berkeley Earth.

So, what happens if we perform the same averaging of station data, but use the raw temperature data without homogenization and breakpoint adjustments? This means first constructing the anomaly data by calculating the MRT using only the actual station data. 

Ideally when calculating the MRT values it is best to choose as long a time interval as possible for the reference average so that those values have less uncertainty associated with them. This means that ideally you want to include as many years of data as possible in the calculation of each of the twelve MRT values. But this poses a number of problems.

(i) Different station records generally have different amounts of data.

(ii) Different station records often encompass different epochs.

(iii) Most station records have periods of missing data or gaps in their record. These may be a single month of data, or they could be several years in length, and there are often multiple gaps.

(iv) Different sets of station data have different temperature trends. Moreover, the longer the temperature records, the more the trend can vary over time within that station record, or the greater the difference in the mean temperatures will be at either end of the record.

The result is that you need to compromise by choosing a time interval for the MRT average that maximizes the total number of stations that can be included in the average, reduces the uncertainty in that average, but also addresses the four issues listed above. The solutions to those four problems are as follows:

(i) Use the same length of time interval for the MRT average for all stations. This is normally 20 or 30 years.

(ii) Choose the MRT time interval so that it overlaps with the epochs of as many station records as possible. In the case of South America this was achieved by using the time interval 1971-2000.

(iii) Set a minimum threshold for the number of years of data required for the MRT for that month to be of sufficient quality. For the data analysed here that was set at 40% (i.e. 12 out of a possible 30 years).

(iv) Set the length of time interval for the MRT average to be shorter than the timescale over which most significant temperature trends are seen. This is normally 20 or 30 years.

Fig. 35.5: The temperature trend for South America since 1832. The best fit is applied to the interval 1900-1999 and has a gradient of +0.54 ± 0.05 °C per century. The monthly temperature changes are defined relative to the 1971-2000 monthly averages.

After the MRT has been calculated for each of the twelve months in each station record, these MRT values are then subtracted from the raw temperature data for that station to yield the monthly anomalies. The anomalies from all the stations are then averaged to provide the regional temperature trend. This trend for South America is shown in Fig. 35.5 above.

The data in Fig. 35.5 clearly shows an upward temperature trend since 1920 of about 0.5 °C. This is similar to trends we have seen in other regions such as Australia and New Zealand, but it is much less than the 1.0 °C or so that is expected based on the HadCRUT4 data. However the picture before 1900 is less clear. There is some evidence of higher temperatures in the late 19th century, but the data is not extensive enough to provide definite proof. There are only about a dozen stations in the whole continent with data that dates from before 1880. Nevertheless, there are definite similarities between the data shown here for South America and other Southern Hemisphere data from Australia and New Zealand. The fact that all three regions exhibit similar trends before 1900 and also after 1900 suggests that the higher temperatures seen in Fig. 35.5 before 1900 are probably real.

What is evident, though, is that the temperature rise in the trend based on the raw data shown in Fig. 35.5 is not as severe as that published by Hadley-CRU, or that published by Berkeley Earth and shown in Fig. 35.4 above. The differences between the two sets of data (from Fig. 35.5 and Fig. 35.3) are highlighted in Fig. 35.6 below.

Fig. 35.6: The contribution of Berkeley Earth (BE) adjustments to the anomaly data after smoothing with a 12-month moving average. The linear best fit to the data is for the period 1901-2010 (red line) and the gradient is +0.33 ± 0.02 °C per century. The orange curve represents the contribution made to the BE adjustment curve by breakpoint adjustments only.

What Fig. 35.6 demonstrates is that the adjustments made to the data by Berkeley Earth are (again) not neutral. In this case they add at least 0.4 °C to the warming since about 1900. But, this is not new. Similar impacts have been seen previously on the temperature trends from many other regions in the Southern Hemisphere (see my other country-based and regional blog posts 8, 18-26, 30-34).

Conclusions

1) There has been about 0.5 °C of warming in South America since 1920. This is much less than is claimed by climate groups and the IPCC.

2) There is some evidence of higher temperatures before 1900, similar to those seen in Australia and New Zealand, but it is heavily dependent on only one or two temperature records, principally Rio de Janeiro as shown in Fig. 35.1.

3) Adjustments made to the data by Berkeley Earth have added significant warming to the temperature trend since 1900.

Addendum

The temperature trend shown in Fig. 35.5 above is the result of averaging almost 300 temperature records. While all these records have over 480 months of data, very few extend back beyond 1900. In fact between 1860 and 1900 the number of temperature records involved in the average for the trend varies from 4 up to 18. This implies an uncertainty in the trend in Fig. 35.5 of between 0.25 °C and 0.5 °C, whereas after 1960 this falls to about 0.05 °C. Thus the uncertainty in the trend in 1860 is about ten times greater than in 1980. This is probably reflected in the differing amounts of natural variation in the 5-year moving average temperature trend for those different epochs. 

It should also be noted that the temperature data shown in Fig. 35.5 before 1860 is dominated by the temperature data from Rio de Janeiro shown in Fig. 35.1. Its reliability is therefore questionable.

Fig. 35.7: The number of sets of station data included each month in the temperature trend for South America shown in Fig. 35.5.

34. South Pacific - temperature trends part 2 (east) COOLING

In my previous post I used the temperature data from all the significant temperature records in the region to show that there is no evidence of anthropogenic global warming (AGW) in the western region of the South Pacific. Now I will demonstrate the same for the eastern region.

The eastern region I have defined to be the part of the southern Pacific Ocean between the Pitcairn Islands at a longitude of about 130.1°W and the Pacific coast of South America. This region of the ocean contains far fewer islands than the western portion, and therefore far fewer temperature records. In fact there are only seven station temperature records with more than 480 months of data, of which two are long station records with more than 1200 months. Those latter two are both located on the Chilean islands of Isla Juan Fernandez (Berkeley Earth ID: 11338 and 153937) along with one of the medium records with over 480 months of data (Berkeley Earth ID: 11341). Of the other four medium records, one is from the Pitcairn Islands (Berkeley Earth ID: 155860), one is from San Cristobal in the Galapagos Islands (Berkeley Earth ID: 154642), and two are from the Chilean island of Isla de Pascua, otherwise known as Easter Island (Berkeley Earth ID: 11362 and 153945).

Fig. 34.1: The temperature trend for the eastern South Pacific since 1900. The best fit is applied to the interval 1913-2012 and has a negative gradient of -0.10 ± 0.06 °C per century. The monthly temperature changes are defined relative to the 1951-1970 monthly averages.

The anomalies for each of the seven temperature records used were calculated by subtracting a monthly reference temperature (MRT) from each monthly reading, as described previously. These reference temperatures were calculated by averaging that month's data for the interval 1951-1970. The mean of the seven sets of anomalies is shown above in Fig. 34.1. It can clearly be seen to exhibit a negative temperature trend. In other words, there is no evidence of global warming.

Fig. 34.2: Temperature trends for all long and medium stations in the eastern South Pacific since 1900 derived by aggregating and averaging the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1913-2012 and has a gradient of +0.71 ± 0.03 °C/century.

Yet the same calculation using Berkeley Earth adjusted data yields a completely different result. The warming since 1900 is now more than 0.8 °C. This is not a consequence of the data, but of the adjustments made to that data. The sum of those adjustments is illustrated below in Fig. 34.3, and indicates that they amount to a correction to the raw data of at least 0.8 °C since 1900, and possibly even more. The data in Fig. 34.3 also indicates that the vast majority of these adjustments are due to the breakpoint adjustment process rather than homogenization.

Fig. 34.3: The contribution of Berkeley Earth (BE) adjustments to the anomaly data after smoothing with a 12-month moving average. The linear best fit to the data is for the period 1913-2012 (red line) and the gradient is +0.81 ± 0.04 °C per century. The orange curve represents the contribution made to the BE adjustment curve by breakpoint adjustments only.

Conclusions

1) The overall temperature trend in the eastern region of the South Pacific over the last 100 years has been negative (see Fig. 34.1). There is no evidence in the raw temperature records of anthropogenic global warming (AGW) in this region.

2) In contrast, the adjusted temperature data constructed by Berkeley Earth exhibits a strong warming trend in its aggregated data of over 0.7 °C per century since 1900 (see Fig. 34.2).

3) The adjustments made to the raw temperature data by Berkeley Earth equate to a change in the overall temperature trend of more than 0.8 °C per century. Almost all of this is the result of adjustments made using the breakpoint adjustment process (see Fig 34.3).

Addendum

The data in Fig. 34.1 above was calculated by averaging the records of the seven stations listed. However, as three of those stations are in close proximity to each other on Isla Juan Fernandez, and another two are likewise in close proximity on Isla de Pascua, it could be argued that relative weightings of 1/3 and 1/2 respectively should be applied to these stations. It so, then the overall temperature trend will change to that shown below in Fig. 34.4. The principal result here is that the new temperature trend with the station weightings is now even more negative: -0.18 ± 0.07 °C per century.

Fig. 34.4: The temperature trend for the eastern South Pacific since 1900. The best fit is applied to the interval 1913-2012 and has a negative gradient of -0.18 ± 0.07 °C per century. The monthly temperature changes are defined relative to the 1951-1970 monthly averages and local weightings are applied to the different temperature anomalies.