If we define the temperature record at a position ri (where i just denotes a label for that location or weather station) on the Earth's surface at time t to be Ti(ri,t), then each temperature record Ti(ri,t) can be thought of as the sum of four distinct components as shown below.
(5.1)
The first of the terms to the right of the equality is the one we are interested in: G(t). This is the global warming trend for the whole planet. It is in effect two terms in one. The first is the benchmark term G(0), which is the global temperature before the start of our measurement, Ti(ri,t). The second is the change in G(t) over time which we can denote as ∆G(t). So
(5.2)
The other terms after G(t) in Eq. (5.1) are (in order), the local warming trend (Li), the seasonal temperature change (Si), and the local random variations (Wi). These last three terms all vary with time (t) and the location (ri). The term Li(ri,t), like G(t), is actually the sum of two terms, one that denotes the value of Li(ri,t) at the start of the temperature record, Li(ri,0), and a second that represents the change of Li(ri,t) with time, ∆Li(ri,t).
Li(ri,t) = Li(ri,0) + ∆Li(ri,t).
(5.3)
The term Wi(ri,t) is just the local weather. It is therefore random and should average to zero, either over time via a temporal moving average on the dataset, Ti(ri,t), or over position if we combine records from different stations across the globe.
The term Si(ri,t) is related to the monthly reference temperature (MRT) that was discussed in the previous post, which we can denote as Mi(ri,t). So we know how to calculate this, by adding a sufficient amount of data from the same month but different years, in the same record and over multiple years, and finding the mean. However this value will inevitably contain the benchmark values of G(t) and Li(ri,t), namely G(0) and Li(ri,0) respectively.
(5.4)
Given that Ti(ri,t) is our data and ∆G(t) or G(t) is what we are trying to measure, the task then is to be able to identify and remove the other three terms Li , Si and Wi. We can do this as follows.
The term Li(ri,t) is the local warming trend. This is how much the local temperature data is changing with time in a manner that is different from G(t). This could be due to differences in latitude, altitude or local geography (such as whether the station is inland or close to the sea, or surrounded by mountains). However, what is also true of Li(ri,t) is that, in absence of any global warming G(t), it should average to a fixed value. But that fixed value would just in effect be a second global warming term that should by rights be part of G(t). In which case it would be logical for the sum of all the local warming terms to equate to zero.
(5.5)
But as already mentioned, the same should be true for the weather component as well:
(5.6)
These two constraints allow us to find the global warming term G(t). To do so we first need to find the temperature anomaly for station or location i.
(5.7)
This, as explained in the last post, is just the difference between the station temperature, Ti(ri,t), and the MRT. If we substitute for Ti(ri,t) and Mi(ri,t) in Eq. 5.7 from the expressions in Eq. 5.1 and 5.4 respectively, together with Eq. 5.2 and Eq. 5.3, after cancellation of terms we get the expression
(5.8)
Now when we sum the anomalies we get
(5.9)
But we know that the summation over Wi(ri,t) will tend to zero as the number of stations increases, or if a smoothing process is utilised, as will the summation over ∆Li(ri,t). So the net result is that if we sum over all possible stations, then
(5.10)
where N is the total number of stations in the summation. Hence the global warming trend is just the mean of the temperature anomalies.
(5.11)
or
(5.12)
If we just sum over all local stations within a region R we will get a similar result, but one that includes the regional trend ∆LR(t).
(5.13)
As the number of regions in the summation increases, the ∆LR(t) term will tend to zero and the result will tend to that in Eq. 5.11. It is important to note, however, that when combining anomalies, those anomalies should be derived using MRTs calculated over the same time period. Typically this is chosen to be from 1961 to 1990, mainly because this period contains data from the largest number of temperature records. A second consideration, though, when choosing a suitable period is to select the one where the temperature is most stable. However, given that most temperature records are fairly recent and recent temperature anomalies tend to show the largest rate of warming, it follows that these two criteria are often mutually exclusive.
What the above analysis demonstrates is that the global warming trend, either globally or locally, is just the sum of the temperature anomalies. None of this requires the climate scientist to determine the local climatic warming Li(ri,t). That is just an additional layer of complexity via which the data may possibly be corrupted or even cynically distorted.
The major caveat that one should apply to the above analysis is that it assumes that all stations are equally important in the summation in Eq. 5.13 or Eq. 5.11. This is generally not true as each station effectively represents the area between itself and its nearest neighbours. Hence stations that are more isolated are, therefore, responsible for a larger surface area and should command a stronger weighting.
To account for this we can give each station a weighting coefficient ai that reflects the proportion of the land area (Ai) that surrounds station i, in comparison to the total land area Atot. Thus if
(5.14)
then
(5.15)
It is also worth noting the because the areas Ai sum to Atot, it follows that the coefficients ai must sum to unity.
So are these weighting coefficients an important consideration? Well most of the major climate science groups that have derived curves for the global warming (NOAA, NASA-GISS, Berkeley Earth and UK Met. Office Hadley Centre/UEA CRU) seem to calculate the area around each station to great precision and use this in the weighting. Personally I think this is generally a waste of effort. I would argue that in most countries the weather stations appear to be fairly uniformly distributed and any variation is relatively small compared to the much larger measurement uncertainties seen in the temperature data. However, there are certainly enormous differences in station densities between countries and also regions (as noted previously), so it is mainly when combining results from different countries and regions that this becomes a major issue, in my opinion.
The main point, however, is this: To get the global warming trend, you just need to average the anomalies. If you do this for a country or a region, the trend will be unique for that country or region. But this will also show you which countries and regions have the greatest warming.



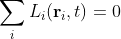
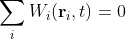


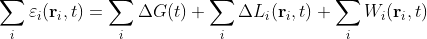






No comments:
Post a Comment