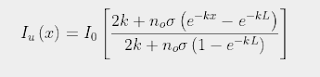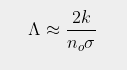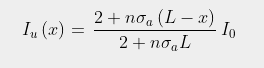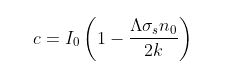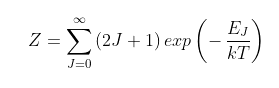126. Lateral thought #6: Is plastic a form of carbon capture or a pollutant?

 

Climate change and environmentalism can be confusing. They can also be contradictory. As an example consider this.

 

Climate change

We are told that fossil fuels are bad for the environment because they produce carbon dioxide (CO₂).

We are told that this CO2 stays in the atmosphere and adds to the greenhouse effect. This in turn increases downwelling radiation which causes global warming.

We are told that we need to prevent global warming by putting less CO₂ into the atmosphere. This means either less use of fossil fuels or removing CO₂ from the atmosphere. As using less fossil fuels is difficult to achieve economically, then maybe we need to look at CO₂ removal.

One suggested removal method is carbon capture. This involves removing the CO₂ from the atmosphere and storing it underground in perpetuity. One way to achieve this could be to turn fossil fuels into a compound of carbon that does not degrade or decompose. Well we have such a set of compounds - they are called plastics. So plastic is a form of carbon capture. So plastic is good, yes?

The environment

Well no, because we are also told that we are polluting our environment with unnatural materials.

One of the worst of these is plastic because it does not decompose. So the trend now is to make plastic biodegradable so that it does decompose. But if it does decompose then it will just add to the carbon in the carbon cycle (see Post 36), first in the soil and then it will add to the amount of CO₂ in the atmosphere.

So biodegradable plastic is good for the environment but bad for global warming. 

Bio-plastic or non-bio?

So there is the dilemma. Plastic could help to permanently store unwanted carbon and prevent it entering the atmosphere, but it could damage the environment instead.

But if we prioritize protecting the environment by making plastic biodegradable, then we will just add the carbon in those plastics to the atmosphere in the form of CO₂.

It appears that there are no easy solutions.

92. The Greenhouse Effect for real atmospheres

In my previous post I showed how Schwarzschild's equation for the absorption and emission of radiation by a gas could result in identical results to a model based purely on elastic scattering. The only conditions on the proof I presented were that the gas is only heated at one end, and that energy conservation applies within the gas; namely that the energy each layer of the gas emits by Planck radiation balances the total energy it absorbs from the two fluxes of upwelling and downwelling radiation, I_u(x) and I_d(x) respectively. I then showed that this leads to a higher transmission through thick layers of greenhouse gas than would be expected based on the Beer-Lambert law.

In this post I will consider two other situations; one where the gas is heated equally at both ends of a long column, and the second where the gas is heated at the bottom and its concentration decreases exponentially with height. The first is analogous to the situation in Antarctica, while the second is a good approximation of how the Greenhouse Effect works on both Earth and Mars.

1) Heating a column of gas at both ends

In Post 91 I showed in Fig. 91.3 how the intensity of radiation travelling in the forward and reverse directions through a greenhouse gas changes with distance into the gas when the gas is heated at one end. In both cases the radiation flow decreases linearly with distance into the gas, with the difference in the forward and reverse fluxes remaining constant. This difference in fluxes decreases with gas concentration and the thickness of the gas layer as illustrated in Fig. 91.4. But suppose the layer of gas is instead heated equally at both ends? What will happen then?

Well the resulting energy flows can be deduced from Fig. 91.3 using a combination of reflection symmetry and superposition and are shown in Fig. 92.1 below.

Fig. 92.1: The relative intensities of transmitted and reflected radiation in a 500 m long column of air with 420 ppm CO₂ that is heated equally from both ends. LT is radiation transmitted from left to right when the heating is at x = 0 m, and LR is the amount reflected. RT is radiation transmitted from right to left when the heating is at x = 500 m, and RR is the amount reflected.

In Fig. 92.1 the curve TL (blue curve) represents the radiation incident from the left at x = 0 m which is then partially reflected by the greenhouse gas to create a reflected flux RL (red curve) that propagates from right to left, building in strength as it propagates. This much is identical to the situation in Fig. 91.3 in the previous post. However, in the case of Fig. 92.1 an identical radiation flux RT also enters the column of gas from the right (green curve). This is also partially reflected by the greenhouse gas to create a reflected flux RR (violet curve) that propagates from left to right. The net result is that there are now two radiation fluxes travelling from left to right (TL and RR), and two travelling in the opposite direction (LR and RT). 

It can then be seen that the total radiation flowing from left to right will be the sum of LT and RR, which will be a constant value of 1.0 at all points along the gas column. The same is true for the total radiation flowing from right to left. In other words, the radiation that is emitted at the right hand exit of the column (x = 500 m) balances exactly the energy that entered initially at x = 0 m. Similarly the radiation that is emitted at the left hand exit of the column (x = 0 m) exactly balances the energy that initially entered at the right (at x = 500 m). This result leads to three important conclusions. 

The first is that in this situation the gas must be isothermal. This follows from the Schwarzschild's equation (see Eq. 91.6 in Post 91). As the total radiation flux in both directions is constant, it follows that the differentials of both I_u(x) and I_d(x) must be zero and so the following equality must hold at all points x.

I_u(x) = I_d(x) = B(λ,T)

(92.1)

As I_u(x) and I_d(x) are both independent of x, then it follows that B(λ,T) must be as well. In which case the temperature T must be independent of x.

The second is that the radiation emitted at each end of the column in not just the radiation that entered at the opposite end. Some of it is radiation that has been reflected by the greenhouse gases via the Greenhouse Effect. This is an important point that is lost on many. It is often falsely claimed that because the gas is isothermal and the radiation flux exiting the gas balances that entering at the opposite end, then this must mean that the Greenhouse Effect is not in operation. Actually it is. It just appears not to be.

The third conclusion is that the Beer-Lambert law cannot be valid in this situation as it cannot explain this result. If the transmitted radiation fluxes LT and RT obeyed the Beer-Lambert law then they would both decay exponentially with distance into the gas, and so too would their reflected fluxes LR and RR. This would mean that the total flux in each direction at the centre of the gas column would be less than at the ends. The laws of thermodynamics cannot allow this to happen as it would lead to a permanent temperature decrease from each end towards the centre. Energy would flow into the centre only to disappear there in violation of the law of conservation of energy. So the Beer-Lambert law is a red herring in this instance.

2) The Greenhouse Effect for Earth's atmosphere

The Earth's atmosphere deviates from the examples I have discussed so far in one major respect: its density, n(x), decreases with height, x. This density change is more or less exponential over most of the lowest 80 km and is of the form 

n(x) = n_o e^-kx

(92.2)

where k = 0.15 km^-1. As the relative concentration of carbon dioxide (CO₂)in the atmosphere is remarkably constant at about 420 ppm for all altitudes up to at least 80 km, it then follows that the CO₂ density will also decay with altitude, x, in accordance with Eq. 92.2 as well with n_o = 0.018 mol/m³. As the atmosphere is mainly heated from the bottom by the Earth's surface this decrease in density with height will significantly effect the nature of the Greenhouse Effect.

The strength of the Greenhouse Effect can be determined by substituting the expression for n(x) shown in Eq. 92.2 into Eq. 91.5 in Post 91. It is then possible to solve for I_u(x) subject to the constraint that the difference between I_u(x) and I_d(x) remains constant for all values of x due to conservation of energy as I explained in Post 88. The result is that I_u(x) varies with x as

(92.3)

where σ is the absorption/emission cross-section of the CO₂ molecules and L is the total height of the atmosphere. It then follows (by setting x = L in Eq. 92.3) that the total amount of radiation emitted at the top of the atmosphere into outer space will be ΛI_o where the emitted fraction Λ is given by

 (92.4)

Subtracting ΛI_o from Eq. 92.3 then gives the associated expression for the downwelling radiation

(92.5)

As the height of the atmosphere, L,  exceeds 80 km, and k is much smaller than n_oσ, it can then be seen that Eq. 92.4 will approximate as

(92.6)

This is virtually identical to the result shown in Eq. 91.10 in Post 91, but with L replaced by 1/k. This is not very surprising as the mathematics of integral calculus tells us that 1/k is the effective thickness of an atmosphere that gets exponentially thinner with increasing height. It also indicates that the amount of radiation that escapes at the top of the atmosphere will decrease inversely (i.e. reciprocally) with CO₂ concentration and not exponentially as predicted by the Beer-Lambert law. This is shown graphically in Fig. 92.2 below where I_u(x) based on Eq. 92.3 at each altitude x is compared to the expected transmission based on the Beer-Lambert law. The difference is striking.

 

Fig. 92.2: A comparison of the amount of 15 µm IR radiation transmitted upwards at different heights in the atmosphere (blue curve) compared to that predicted by the Beer-Lambert law (red curve).

What Fig. 92.2 shows is that the amount of 15 µm radiation escaping at the top of the atmosphere is much greater than many people think. According to the Beer-Lambert law it should be so low as to be unmeasurable. In reality it could be as much as 1.5%. The blue curve in Fig. 92.2 does fall exponentially, but not to zero: it tends asymptotically to Λ. The value of Λ also depends on the nature of the atmosphere as Eq. 92.4 shows. However, its dependence on CO₂ concentration is reciprocal not exponential. This is why more radiation escapes than many people intuitively think can do.

Summary

The examples outlined in this post show that the Greenhouse Effect is more complex than the simplistic model that is generally presented. Even thick layers of greenhouse gas will emit appreciable amounts of infra-red radiation from within their absorption bands. Relying on the Beer-Lambert law will result in at best an incomplete picture, and at worst a totally misleading one.

Yes, the amount of IR radiation transmitted by the Earth's atmosphere reduces exponentially with height, at least at lower altitudes, but this is not due to its absorbing properties associated with the Beer-Lambert law. It is due primarily to the exponential drop in CO₂ concentration with height. Even then this exponential fall never tends to zero as Eq. 92.3 and Eq. 93.4 demonstrate, but instead tend to a finite transmission value Λ that could be as much as 1.5%.

91. The Schwarzschild equation and scattering

In Post 86 I showed how the Greenhouse Effect can be viewed as resulting from a combined process of absorption of infra-red radiation by molecules of carbon dioxide (CO₂), followed by re-emission of the same wavelength of radiation, but in a different random direction. The law that leads to this result is the principle of detailed balance. I also showed how this process resembled a scattering process, but with a much greater strength due to the significantly greater absorption cross-section (σ_a) of CO₂ compared to its cross-section for Rayleigh scattering, σ_s. Therefore it could be modelled as a scattering process, but one with an appropriately large cross-section.

Then in Post 88 I showed how this combined process of absorption and re-emission resulted in absorption that decreased linearly with distance x into a gas of uniform density, rather than exponentially as predicted by the Beer-Lambert law. The importance of this result is that it demonstrates that the transmission of radiation through an absorbing gas will be greater than that predicted by the Beer-Lambert law, and so changes to the concentration of the absorbing gas will have a larger impact on the overall transmission than the Beer-Lambert law would predict. 

Sadly this result has been questioned by some who have claimed that the scattering (or combined absorption and re-emission) approach is not valid as it does not follow from, or agree with, Schwarzschild's equation. This equation is possibly named after the German physicist Karl Schwarzschild (shown below), although it could actually be named after his son Martin Schwarzschild who worked in the field of stellar evolution. In this post I will show that this claim of non-validity is not true and that Schwarzschild's equation leads to the exact same results as I outlined in Post 88.

 Fig. 91.1: Karl Schwarzschild (1873-1916)

The Model

In order to understand the Greenhouse Effect we need to consider the radiation flows through a thin layer of gas of thickness δx at some altitude x, and then extend this to model to the gas as a whole. In particular, we need to consider radiation flows through the gas from opposing directions. This is because each thin layer of the gas only absorbs a small fraction of radiation passing through it. Most of the rest is then absorbed by subsequent layers above the initial layer. However, after absorption the radiation is re-emitted and the re-emission process occurs equally in both directions (up and down). This means that some of this emitted radiation will travel in a downwards direction and reheat the first layer from the opposite direction. This is why the Beer-Lambert law fails.

In order to model this process we need to consider radiation fluxes in both directions as shown in Fig. 91.2 below. Let's assume that the gas has a concentration or particle density n(x), and each molecule of it has an absorption cross-section σ_a. If radiation of intensity I_u(x) travels in an upward direction from a hot surface and enters the gas layer from below, as shown in Fig. 91.2 below, a proportion of it will be absorbed by the gas. This in turn will heat the gas and cause it to emit radiation in both an upwards and a downwards direction. The result will be that the intensity of upward radiation leaving the gas layer will change by an amount δI_u(x).

Fig. 91.2: A schematic illustration of how scattering, absorption and thermal emission within each thin layer of the atmosphere alters the intensities of the upwelling (I_u) and downwelling (I_d) radiation.

The upwelling radiation will then go on to interact with gas above the layer shown in Fig. 91.2 and thus heat this gas as well. This gas will then re-emit radiation, some of it in a downward direction, and this downwelling radiation I_d(x) will then also pass through our original layer of gas. It in turn will be partially absorbed, heating the gas and causing it to radiate. The net result is that the intensity of the downwelling radiation leaving the gas layer will also change, in this case by an amount δI_d(x). So far this model is identical to the one outlined in Post 88. The next step is to consider the changes of intensity, δI_u(x) and δI_d(x), using Schwarzschild's equation and the Planck function, B(λ,T), where λ is the wavelength of the radiation and T is the temperature of the gas in kelvins at this height x. In the following discussion I will consider the absorption and re-emission of radiation at a fixed wavelength λ.

The Proof

As the upwelling radiation I_u(x) at a fixed wavelength λ passes through the thin layer of gas of thickness δx a small amount of it will be absorbed by the gas. This amount will be proportional to the number of molecules encountered per unit area, n(x)δx, their absorption cross-section, σ_a, and the amount of radiation in the original flux, I_u(x). The result is that the transmitted intensity will decrease by an amount equal to I_u(x)σ_an(x)δx.

At the same time the thin layer of gas will be emitting radiation in both the upward and downward direction due to its temperature T. This temperature will in turn vary with height x, so both B(λ,T) and I_u(x) will vary with x. The intensity emitted in each direction is given by the Planck function, B(λ,T), multiplied by the number of molecules per unit area in the layer, n(x)δx, and the emission cross-section, σ_e. The result of this emission process is that the transmitted intensity above the layer will increase by an amount equal to B(λ,T)σ_en(x)δx.

Combining these two effects of emission and absorption gives the total change in intensity of the upwelling radiation

δI_u(x) = [B(λ,T)σ_e - I_u(x)σ_a]n(x)δx

(91.1)

This is Schwarzschild's equation. However, it is only half the solution because there is a similar equation that can be derived for the changes to the downwelling radiation I_d(x) in the thin layer at the same wavelength λ. Thus the resulting equation will be

δI_d(x) = [B(λ,T)σ_e - I_d(x)σ_a]n(x)δx

(91.2)

Finally, there is one other consideration we must take into account: energy conservation at wavelength λ. The total energy flowing into the layer of gas must match the energy flowing out. This means that 

δI_u(x) + δI_d(x) = 0

(91.3)

and so

[ I_u(x) + I_d(x) ]σ_a = 2B(λ,T)σ_e 

(91.4)

We can now eliminate B(λ,T)σ_e from Eq. 91.1 and Eq. 91.2 and turn both equations into first order differential equtions. However, because the change in downwelling radiation I_d(x) in Fig. 91.2 is defined to be positive for changes of x in a negative direction the δx term must be negative, and therefore the differential term dI_d/dx = - δI_d/δx.This means that

 (91.5)

It then turns out that Eq. 91.5 is identical to Eq. 88.5 in Post 88. So if the equations are the same and the boundary conditions are the same, then the solutions must be the same as in Post 88. So even using Schwarzschild's equation as our starting point we end up with the same result. 

Finally, we can write Schwarzschild's equation as two differential equations, one for I_u(x) and one for I_d(x). From Eq. 91.1 we get the obvious result

(91.6)

The equivalent equation for I_d(x) is similar, but requires some explanation.

(91.7)

In Eq. 91.7 the order of the I(x)σ_a and B(λ,T)σ_e terms to the right of the equality sign have been reversed compared to Eq. 91.6. This is because the downwelling radiation, I_d(x), is flowing in the negative direction through the thin gas layer. So for I_u(x) the radiation term B(λ,T)σ_e is directed in the same direction as I_u(x) so it must be positive, while the absorption in the gas layer must leads to a lower value of I_u(x) above the layer than below. In the case of I_d(x) the reverse it true in both cases, hence the reversal of sign for both terms.

Finally, it should be noted that conditions of thermal equilibrium generally require the cross-sections σ_a and σ_e to be equal. This is particularly true for black body radiation where a black body at constant temperature must emit what it absorbs, otherwise it will gain or lose energy, and thus not be at constant temperature.

 

Implications

If we now apply the above results to a real system and consider the case of a column of gas of thickness L, and uniform density n that is independent of x, the model outlined above means that the upwelling radiation will vary with x through the gas as (see Post 88)

(91.8)

where I_o is the intensity of radiation entering the gas at x = 0, while the downwelling radiation will vary as

(91.9)

The difference between I_u(x) and I_d(x) will be constant (ΛI_o), as required by energy conservation, and will be equal to the amount transmitted at the end of the column (i.e. at x = L), so 

(91.10)

In Fig. 91.3 below I have suggested what I_u(x) and I_d(x) might look like through a 500 metre long horizontal column of air with 420 ppm of CO₂ when it is irradiated with 15 µm infra-red radiation from one end. It should be noted, though, that this theoretical data is based on an estimated value for the scattering cross-section of the CO₂ molecules that could be almost a factor of ten too small. Nevertheless, it still illustrates qualitatively how the transmission of 15µm infra-red radiation changes through the gas, and also how the Greenhouse Effect (as defined by the relative intensity of the reflected radiation at x = 0) is related to this transmission (see the red curve in Fig. 91.3).

Fig. 91.3: The relative intensities of transmitted (I_u) and reflected (I_d) radiation along a 500 metre column of air containing 420 ppm of CO₂ with an absorption cross-section of 1.6 x 10^-24 m².

The graph in Fig. 91.3 suggests that a 500 metre column of air will transmit less than 18% of the incident radiation and reflect back the rest. The question is: is this more or less than that predicted by the Beer-Lambert law? The answer to this can be seen in Fig. 91.4 below.

Fig. 91.4: The relative intensities of radiation transmitted  through a column of air of length L containing 420 ppm of CO₂ with an absorption cross-section of 1.6 x 10^-24 m² based on two different models: (i) a backscattering model described by Eq. 91.10 (blue curve), and (ii) the Beer-Lambert law (red curve).

The blue curve in Fig. 91.4 demonstrates how the transmission through a column of air would decrease with the length of the column, L, if half of the absorbed radiation is backscattered or re-emitted in the reverse direction and half is re-emitted in the forward direction. The result is a curve that decays with L in accordance with Eq. 91.10. The red curve on the other hand shows how the transmission would change if it followed the (commonly accepted) Beer-Lambert law where the transmitted intensity varies with L as

(91.11)

What is clear is that the Beer-Lambert law underestimates the transmission for large values of L, and in effect predicts that there is no significant transmission beyond 400 metres. The blue curve shows that this is not the case with over 10% transmission for a column of length 1000 metres. In practice this means that the Beer-Lambert law will massively underestimate the impact of future increases in CO₂ levels because it will assume that the backscattering is already operating at close to 100% or saturation with 420 ppm of CO₂. Yet clearly it is not. In fact even at 10 km (the effective thickness of Earth's atmosphere) there is still more than 1% transmission. While this is small, it is not insignificant, particularly when considering the relatively small changes to the overall size of the Greenhouse Effect that are needed to create a warming of 1.5°C.

Caveats

The only condition I have applied to the proof and discussion described here is that set out in Eq. 91.4, which basically demands that each layer of the gas radiates the same amount of energy at each wavelength as it absorbs from the two fluxes, I_u(x) and I_d(x). This will be true provided all the heat of wavelength λ entering the gas originates from the Earth's surface at the bottom of Fig. 91.2, or at the very top of the atmosphere. In which case, the exact functional forms of I_u(x) and I_d(x) will depend only on the functional form of n(x) and the boundary conditions. However, at the top of the atmosphere this condition will not be satisfied as some of the incoming ultraviolet radiation from the Sun is absorbed there before it reaches the ground and so gets converted to infra-red radiation within the upper atmosphere. This means that Eq. 91.4 is no longer satisfied for each and every infra-red wavelength of interest within the gas.

In my next blog post I will consider a number of distinct and important examples to demonstrate how dependent the transmission is on the density profile of the gas, n(x), and also on the location of the heat source(s). These examples will also show that even when it sometimes looks like there is no Greenhouse Effect in operation, it is still there.

89. The Greenhouse Effect on Mars

In my previous three posts I have explained how the Greenhouse Effect (GHE) works on Earth, and how it is affected by changes to the carbon dioxide (CO₂) concentration in the atmosphere. The problem with studying the GHE on Earth, though, is that its operation is complicated by the presence of large amounts of water vapour in the atmosphere. As water vapour also has a broader absorption band and higher atmospheric concentration than CO₂, this means that changes in the CO₂ concentration are less important than they would be otherwise. If we want to understand and measure the GHE just due to carbon dioxide, then we need an environment with high levels of CO₂ but low levels of other greenhouse gases. In this respect one of the best places to study is Mars. 

The Atmosphere of Mars

The Martian atmosphere has some similarities with Earth but many differences. It contains many of the same gases (nitrogen, oxygen, water vapour, argon, CO₂), but the proportions are vastly different. The atmosphere of Mars is 96% CO₂ with about 2% nitrogen and 2% Argon (although different pages on Wikipedia give slightly different values such as 95% CO₂ and 3% nitrogen). There are also trace levels (< 0.1%) of other gases such as water vapour (210 ppm) and oxygen (0.15%). 

The other main difference in terms of the atmosphere is the pressure at the surface. At 610 Pa this is only 0.60% of the surface pressure on Earth, and as about 96% of this is CO₂, this means that there is a surface density of 3610 mol/m² of CO₂ on Mars compared to only 150 mol/m² on Earth. So any outgoing radiation from the surface of Mars has 24.06 times as much carbon dioxide gas to penetrate, in order to escape into outer space, compared to on Earth. What this means in practice is that the Greenhouse Effect in the Martian atmosphere should be easier to analyse because it can only have one source - CO₂.

 

The Energy Balance for Mars

Mars is also approximately 52% further from the Sun than is Earth, so one might expect that to mean that its surface is colder. This is true, but not as much as it should be based on distance alone. 

The solar radiation flux entering the Martian atmosphere is only 586 W/m² compared to the 1360 W/m² that irradiates the Earth. As this radiation is spread over a surface area (4πr²) that is four times greater than the cross-sectional area of the planet (πr²) in each case, this means that the average radiation flux at the Martian surface is 143.5 W/m². Yet this is only 22% less than the 184 W/m² that reaches the Earth's surface. This is because nearly 50% of incident radiation on Earth is either reflected by clouds or is absorbed by ozone and water vapour in the upper atmosphere. But there are no clouds, ozone or significant water vapour on Mars.

Then there is the issue of surface albedo or Bond albedo. This is the proportion of incident radiation that is reflected by the planet back out into space without being absorbed, either from clouds or the surface. For Earth this is about 31%; for Mars it is only 25%. This means that the average surface absorption on Mars is 108 W/m² compared to 161 W/m² on Earth. So while Mars only receives 43% of the solar radiation that Earth does, after absorption and reflection the Martian surface receives 67% of the radiation that the Earth's surface does. That is a relative increase of more than 50% for Mars which partially compensates for its greater distance from the Sun.

Calculating the Surface Temperature of Mars

If we now invoke the Stefan-Boltzmann law (see Eq. 13.1 in Post 13),

I = σT⁴

(89.1)

where I is the surface radiation flux, σ is the Stefan-Boltzmann constant, and T is the surface temperature in kelvins, we see that a surface radiation flux of 108 W/m² equates to a mean surface temperature on Mars of 209 K (or -64°C). Yet the true mean temperature is thought to be about 215 K (or -58°C). The difference is due to the Greenhouse Effect. 

For comparison, on Earth a solar flux at the surface of 161 W/m² would equate to a mean surface temperature of 231 K (or -42°C), yet the true mean temperature is about 289 K (or +16°C). So the GHE on Earth adds 58°C of warming while on Mars it only adds 6°C. Yet there is almost twenty-five times more carbon dioxide on Mars (3690 mol/m²) than on Earth (150 mol/m²), so you would expect the greenhouse effect due to CO₂ to be stronger. But how much stronger? The answer is: not very. In fact it is significantly less than the actual measured value on Earth.

Calculating the Strength of the GHE on Mars

In Post 87 I showed how the width of the CO₂ absorption band at 15 µm can be determined using the known concentration of CO₂ (N_o), its scattering or absorption cross-section (σ_s), the quantized frequency of rotation of the CO₂ molecules (B), and the temperature (T). From this it is possible to estimate the critical CO₂ concentration needed to absorb most of the infra-red radiation (N_th). The term N_th can be estimated to be 0.5 mol/m² based on the value of σ_s, while N_o will be about half the total CO₂ concentration, so N_o = 1845 mol/m². From this we can estimate the maximum number of excited rotational states in the absorption band, J_th, using (see Post 87)

(89.2)

where k is Boltzmann's constant, h is Planck's constant and Z is a normalization constant (see Eq. 87.2 in Post 87) equal to 185.5 in this case. The ratio term kT/hB has the value 185.3 (as hB = 0.1 meV and T = 215 K) and is always approximately equal to the Z value. 

The result we obtain is that J_th = 36.3, which, given that the spacing of the bands is 0.2 meV, means that the absorption band has a width of 14.52 meV and extends from a wavelength of 13.78 µm to 16.44 µm. This compares to a calculated range of 14.00 µm to 16.14 µm for the same band on Earth, although the measured width on Earth is actually found to be from about 13.35 µm to 17.35 µm. So even though the calculated width of the 15 µm absorption band for Mars is slightly larger than the equivalent for Earth, it is not significantly greater. But it is significantly less than the measured band width on Earth.

 

Fig. 89.1: The electromagnetic emission spectrum for the surface of Mars at a mean temperature of 215K (blue curve) together with the absorption profile due to CO₂ between 13.78 µm and 16.44 µm (red curve).

The impact of the high Martian atmospheric CO₂ concentration on the radiation feedback is demonstrated in Fig. 89.1 above. The red curve indicates the proportion of the outgoing infra-red radiation (blue curve) that is reflected by the CO₂ molecules and it amounts to f = 12.5%. This is slightly more than the 10% seen for the GHE due to backscattering from CO₂ on Earth (see Post 87) despite the absorption band being further from the peak in the emission spectrum due to the lower surface temperature on Mars.

Calculating the Temperature Rise

The radiation feedback of  f = 12.5% shown in Fig. 89.1 equates to a 14.3% increase in the surface radiation and also of T⁴ (because of Eq. 89.1), which then equates to a 3.4% increase in T. So if the initial surface temperature on Mars without the GHE was 209 K, the temperature with the GHE included will be 3.4% greater, or 216.1 K. This means that the temperature rise at the surface due to the Greenhouse Effect is expected to be 7.1 K, which is pretty close to the observed value of around 6 K (or 6°C). The reason for the small difference could be the limited availability of accurate Mars temperature data, or the uncertainty in the value of the CO₂ absorption cross-section, σ_s.

We know how much radiation from the Sun is arriving at Mars to high accuracy, but knowing how much is being absorbed by the planet surface is more difficult as this depends on an accurate measurement of the Bond albedo. However, conventional astronomical telescopes should be able to measure the reflected radiation to pretty good accuracy as well. That allows us to estimate the expected mean surface temperature without the GHE to fairly high precision. The problem is knowing what the actual surface temperature is with the GHE in operation. This is a difficult enough calculation to do on Earth where we have over 16,000 weather stations measuring the surface temperature on a daily basis, and numerous satellites in orbit. Sadly, none, or very little, of this exists for Mars.

So far in this blog post I have assumed a value of 215 K for the mean surface temperature of Mars, but some reports have put it as high as 225 K (or as low as 210 K). In which case Z = 194.15 and J_th = 37.0. This leads to a 15 µm band stretching from 13.76 µm to 16.47 µm, and a feedback factor of f = 13.0%. Under these circumstances the warming from the Greenhouse Effect increases slightly, but only to 7.7°C. 

 

A Comparison with Earth

For comparison, it is instructive to hypothecate the extent of warming on Earth if its atmosphere also contained 3690 mol/m² of CO₂. In that case Z = 249.3 and J_th = 41.6, which leads to a 15 µm band stretching from 13.62 µm to 16.67 µm, and a feedback factor of f = 14.1%. The resulting predicted temperature rise due to CO₂ would be 10.74 K, which is 3.26°C less than the 7.48°C rise currently predicted for Earth as was shown in Post 87). So a twenty-five fold increase in the CO₂ concentration would only result in a 3.26°C temperature increase, although as I showed in Post 87, masking by water vapour would probably reduce this by 75% to only 0.8°C. 

It is a point of note that the density of CO₂ molecules on Mars (3690 mol/m²) is more than double the combined density of all the greenhouse gases on Earth (1560 mol/m²), yet it results in a temperature rise of 5°C - 7°C that is almost ten times less than the 58°C observed for Earth. This is mainly because most of the GHE on Earth is due to water vapour as the width of the CO₂ absorption band is so much less than that for water vapour. Even increasing the concentration of CO₂ on Mars by a factor of twenty-five cannot appreciably change this.

Summary and Conclusions

What I hope I have shown in this post is that Mars is a good test bed for studying the Greenhouse Effect (GHE). Knowing only its albedo, the atmospheric concentration of CO₂, and the intensity of radiation arriving from the Sun, it is possible to accurately predict the temperature rise due to the Greenhouse Effect. This I have predicted to be about 7°C, in close agreement with the current estimate based on observational data (6°C). And this is despite the significant uncertainty over the true measured value of the mean surface temperature on Mars.

The reduced GHE on Mars relative to the Earth occurs despite its much higher (i.e. 24 times greater) atmospheric CO₂ concentration. This in turn suggests that the increasing levels of atmospheric CO₂ we are currently seeing on Earth will produce only slight temperature increases in the future. 

Yes, Mars has its own complicating factors. Heat retention on Mars is limited by the thin atmospheric blanket compared to Earth. This means that the planet does not retain heat very well, but conversely it means that the atmosphere will warm quickly when heated by the Sun. For this reason it may be better to consider Mars under direct solar illumination in daytime. Under these conditions the peak solar flux at the surface of Mars will be four times greater than stated above, or 432 W/m². This will equate to a peak surface temperature of 295 K (or +22°C). Yet the actual maximum temperature is reported to be around 303 K to 308 K (or +30°C to +35°C). So on this measure the warming from the Greenhouse Effect in daytime near the equator appears to be in the range 8°C to 13°C. Yet the predicted value based on a calculation of the width of the 15 µm absorption band is found to be 10.9°C, in other words in the mid-range of the observed values. Once again this is still much less than the total warming seen on Earth and comparable to the contribution to Earth's GHE seen just from CO₂.

88. A scattering model of The Greenhouse Effect

In my two previous posts I analysed the structure of the 15 µm absorption band for carbon dioxide (CO₂) in order to demonstrate how increasing the concentration of CO₂ in the atmosphere increases the the band's width. This widening of the absorption band then slightly increases the proportion of infra-red radiation that is reflected back to the Earth's surface and thus increases the strength of the Greenhouse Effect, thereby increasing the surface temperature. As a result I showed that this enhancement is unlikely to contribute more than about 0.5°C to the strength of global warming, and probably contributes less than 0.2°C; i.e. much less than the 1.2°C that is claimed.

In this post I will consider a different impact of an increase to the atmospheric concentration of CO₂ by calculating the strength of the backscattering at the centre of the 15 µm absorption band. This will involve describing the mathematical and statistical basis for the Greenhouse Effect, and how it arises from the backscattering of photons by greenhouse gas molecules. As a result I will show just how little infra-red radiation within the 15 µm band can escape through the atmosphere, and so also show just how insensitive the backscattering and transmission of infra-red radiation are to further increases in the CO₂ concentration. Finally, I will calculate the expected temperature change for an increase in atmospheric CO₂ concentrations from 280 ppm to 420 ppm, and show that it is significantly less than 0.1°C.

How the scattering process works

The origin of the Greenhouse Effect is the interaction of infra-red photons with air molecules, specifically those of carbon dioxide (CO₂) and water vapour (H₂O). While all air molecules, including those of both oxygen and nitrogen, are capable of scattering infra-red photons via the process of Rayleigh scattering, this scattering is so weak at infra-red wavelengths that it is unimportant. In fact in Post 86 I showed that Rayleigh scattering at wavelengths of 15 µm is a million times weaker than that seen for visible light and which gives the daytime sky its blue colour.

Instead, the dominant process is one of absorption and re-emission of photons where air molecules absorb radiation, and then re-emit it in a random direction. This is only important at wavelengths that match both the peak in the thermal emission spectrum of the Earth's surface (from about 5 µm to 100 µm) and the excitation energies of the molecules. As only CO₂ and H₂O of the main components of the atmosphere have excitation energies that match the peak region of the thermal emission spectrum of the Earth's surface, they are the most important greenhouse gases.

As I showed in Post 86, the combined absorption and re-emission process results in radiation received from one direction (i.e. the Earth's surface) being redistributed in all directions with equal probability. This is because the time delay between absorption and re-emission means that the orientation of the emitting molecules could be in any random direction. The result is a process that looks just like random scattering, and because the direction of scattering is random it is determined by statistical probability.

One way to visualize the backscattering process is by considering the photons of outgoing infra-red radiation as particles that, every so often, collide with greenhouse gas molecules, and bounce off them at random angles. We can define the average distance photons travel between these collisions as the mean free path. At each collision half the phonons will be reflected back in the opposite direction from which they came, while the other half will be scattered forward. But eventually those that are scattered forward will collide with another molecule and half of those will also be backscattered. This process continues as the remaining forward scattered photons travel further into the medium or gas with more and more being reflected. The result is that, eventually almost all the photons have been reflected back, and virtually none are travelling in the original forward direction. This is how the backscattering process works.

It is important to acknowledge, however, that the real process that is occurring is not a backscattering one. The infra-red photons are actually being absorbed by CO₂ molecules which then become excited. They may then transfer this energy to other air molecules via collisions, but eventually those other air molecules will transfer the energy back to the CO₂ and the CO₂ molecules will re-emit it in some random direction. The time this process takes could be quite long, or very short, but it is happening so often that it will appear almost instantaneous. And therefore it will look just like scattering. 

The mathematics of scattering

In order to gauge the importance of this process we need to quantify it. That means defining the process mathematically. By doing so we will be able to see which factors affect the amount of backscattering, and in particular, how it depends on the thickness of the atmosphere and its CO₂ concentration.

In order to do this we must first construct a model of the atmosphere and consider a thin horizontal layer of the atmosphere of thickness δx at some arbitrary altitude x as shown in Fig. 88.1 below. In this model the density of carbon dioxide molecules is n(x), the intensity of the upwelling (or outgoing) radiation at a height x is I_u(x), and the intensity of the downwelling (or backscattered) radiation at the same height is I_d(x). 

Fig. 88.1: A schematic illustration of how scattering within each thin layer of the atmosphere alters the upwelling (I_u) and downwelling (I_d) intensities.

 

In thermal equilibrium the atmosphere will emit the same number of photons each second that it absorbs. This is the origin of the scattering process. Conservation of energy then dictates that the difference between I_u(x) and I_d(x) must be the same at all heights, x, and equal to the total intensity transmitted at the top of the atmosphere. It therefore follows that 

I_u(x) - I_d(x) = I_oΛ

(88.1)

where Λ is the effective total transmission coefficient of the atmosphere and I_o = I_u(0) is the total intensity of radiation emitted at the surface.

Now we consider the change in intensities of I_u(x) and I_d(x) as the radiation passes through the thin layer of thickness δx at height x (see Fig. 88.1 above). In each case there is a probability δp that each photon will be scattered where

δp =  n(x)σ_sδx

(88.2)

and σ_s is the scattering (or absorption) cross-section of the CO₂ molecule at the particular wavelength of the radiation being considered. For each photon that is scattered, half will be scattered forwards and half will be scattered backwards. This means that the value of I_u(x) will decrease by ½I_u(x)δp but increase by ½I_d(x)δp due to the backscattering of the reflected photons in I_d(x). For I_d(x) the opposite will be true. It therefore follows that the change in I_u(x) for a positive increase in x of δx will be

δI_u(x) = ½[I_d(x) - I_u(x)]n(x)σ_sδx

(88.3)

while the change in I_d(x) for a positive increase in x of δx will be (note the extra negative sign)

δI_d(x) = -½[I_u(x) - I_d(x)]n(x)σ_sδx

(88.4)

These results can be written in differential form as

 

(88.5)

The solution to Eq. 88.5 will depend on the distribution of the CO₂ molecules within the atmosphere, n(x), and the boundary conditions. The first boundary condition is I_u(0) = I_o and sets the amount of radiation that initially enters the atmosphere from the surface. The second is I_d(h) = 0 where h is the height of the atmosphere, and this states that once the radiation leaves the top of the atmosphere there can be no more backscattering. The final piece of information we need is the dependence of the CO₂ concentration on altitude, n(x).

The simplest model is to assume n(x) is constant (and equal to n_o) and thus independent of x. This is a fairly good approximation for the lower part of the troposphere and it is one I shall use as a starting point for the analysis. 

 

Transmission coefficient for a gas of uniform density

From Eq. 88.1 we can see that I_u(x) - I_d(x) must be a constant. As n(x) is a constant, Eq. 88.5 dictates that the first differentials of both I_u(x) and I_d(x) must be constant as well. It therefore follows that

(88.6)

The solution for I_d(x) must then be of the form I_d(x) = a(h - x) to satisfy both Eq. 88.6 and the boundary condition I_d(h) = 0, while Eq. 88.5 demands that a = ½ΛI_on_oσ_s. So

I_d(x) = ½ΛI_on_oσ_s(h - x)

(88.7)

The only unknown term is Λ, but we can determine it from Eq. 88.1 and the boundary condition for I_u(0) = I_o. 

From Eq. 88.1 we see that I_u(x) = a(h - x) + I_oΛ, which means that at x = 0 the condition I_o = ah + I_oΛ  must hold. This means that the fraction of radiation that is transmitted at the top of the atmosphere, Λ, is given by

(88.8)

If n_oσ_sh >> 2, then Λ ≈ 2/n_oσ_sh.

It also means that I_u(x) will have a negative linear dependence on x when x < h as follows

 (88.9)

while for x > h we find that the transmitted intensity is I_u(x) = I_oΛ. This negative linear dependence is very different from the exponential decay that is usually associated with pure absorption or attenuation of radiation and described by the Beer-Lambert law.

Knowing Λ allows us to estimate the percentage of infra-red radiation within the 15 µm absorption band that escapes through the atmosphere for different CO₂ concentrations, n_o. A CO₂ concentration of 280 ppm (as existed before 1750) equates to a CO₂ molecular concentration of n_o = 0.0118 mol/m³. The effective thickness of the atmosphere (h) at uniform density is approximately 10 km, while the scattering cross-section (σ_s) was estimated at around 1.6 x 10^-24 m² in Post 87. This gives a value for Λ of 1.67%. But if we instead consider a CO₂ concentration of 420 ppm (as exists today), n_o = 0.0177 mol/m³ and Λ = 1.12%. So an increase in the CO₂ concentration from 280 ppm to 420 ppm leads to the proportion of radiation being reflected by the 15µm CO₂ absorption band increasing from 98.33% to 98.88%. This will lead to a (small) increase in the surface temperature which we can now estimate.

In Post 86 I showed that the width of the 15 µm band typically extends from about 13.35 µm to 17.35 µm and thus reflects about 18.1% of all the infra-red radiation emitted by the Earth's surface. But that assumes that the reflectivity of the band is 100%. In fact it is only 98.88%, having risen from 98.33% due to the increase in atmospheric CO₂. This means that the increase in CO₂ will, in effect, have caused the feedback factor, f, to rise from 18.0% to its current value of 18.1%. We can then use this information, together with the Stefan-Boltzmann law, to determine the change in the surface temperature as we know that 1-f is inversely proportional to T⁴. What we find is that the temperature rise associated with this increase in reflectivity (and hence increase in f) is less than 0.09°C. In fact the actual rise will be probably be less than half this value due to the masking effect of the water vapour.

Result: Increasing the CO₂ concentration from 280 ppm to 420 ppm results in a global temperature increase of less than 0.09°C.

 

Transmission coefficient for a real atmosphere

The analysis so far has assumed that the atmosphere has a finite thickness of constant density that is independent of altitude. This, though, is not true for Earth. The increasing gravitational potential energy with increasing altitude means that fewer molecules have sufficient energy to reach high altitudes. The result is that the density of air decreases with height, and that dependence on height is exponential.

As carbon dioxide molecules are about 50% heavier than those of oxygen and nitrogen one might expect even fewer CO₂ molecules to be present by percentage at high altitudes, but this is not the case. The mixing ratio does not appear to change significantly with altitude. So if there are 420 molecules of CO₂ in every one million molecules of air at sea level, the same is true at heights of 10 km, 25 km, and 50 km. It is just that there are fewer numbers of all molecules at those altitudes.

Over the bottom 80 km of the atmosphere the molecular density, n(x), varies with altitude (x) as

n(x) = n_o e^-kx

(88.10)

where k = 1.4 x 10^-4 m^-1. The same dependence is seen for CO₂ with n_o = 0.0177 mol/m³ for an atmosphere containing 420 ppm of CO₂, and n_o = 0.0118 mol/m³ for an atmosphere containing 280 ppm of CO₂. The dependence of molecular density on altitude changes some of the mathematics outlined in the previous section, but both Eq. 88.1 and Eq. 88.5 will remain unaffected. The first change is to substitute Eq. 88.10 into Eq. 88.5 to give

(88.11)

It therefore follows that I_u(x) is given by

(88.12)

where c is a constant of integration. In which case I_d(x) will be

(88.13)

The values of c and Λ will be dictated by the boundary conditions, I_u(0) = I_o and I_d(h) = 0, which are the same as before. Consequently, the results for c and Λ are

(88.14)

and

(88.15)

It can be seen that if kh << 1, then Eq. 88.15 reduces to the same approximate form as Eq. 88.8, and so both the reflectivity and the temperature rise will be the same as before (see previous section). The more realistic scenario, though, is for kh >> 1, particularly if h > 80 km (in which case kh = 11.2). Then Eq. 88.15 reduces to

(88.16)

which if n_oσ_s >> 2k, then becomes Λ ≈ 2k/n_oσ_s. We can now calculate the expected temperature rise by following a similar procedure to that outlined at the end of the previous section. 

If n_o = 0.0118 mol/m³ (equivalent to a CO₂ concentration of 280 ppm), then Λ = 0.0232 and so 97.68% of the radiation at 15 µm is being absorbed and then reflected. However, if n_o = 0.0177 mol/m³ (equivalent to a CO₂ concentration of 420 ppm), then Λ = 0.0156. This means that an increase in the CO₂ concentration from 280 ppm to 420 ppm leads to the proportion of radiation being reflected by the 15µm CO₂ absorption band increasing from 97.68% to 98.44%. Given that the feedback factor for the 15 µm band is currently f = 0.181, this suggests that the previous value was 0.1796.

As the current mean temperature is 289 K, and the temperature must have increased by a factor of [ (1 - 0.1796)/(1 - 0.181) ]^1/4 due to the change in feedback factor, then the corresponding temperature rise must be only 0.12°C. Once again the masking effect of absorption by water vapour in the same frequency range as CO₂ will probably halve the real value of f from CO₂ . So a large increase in the CO₂ concentration will probably have less than half the effect on the mean global temperature than is stated here.

Result: Increasing the CO₂ concentration from 280 ppm to 420 ppm results in a global temperature increase of less than 0.12°C.

Conclusions

1) Increasing the atmospheric CO₂ concentration from 280 ppm to 420 ppm results in the infra-red transmission through the 15 µm absorption band reducing from 2.32% to 1.56%.

2) This leads to the 15 µm band reflecting back an extra 0.76% of the radiation within the borders of the band. But as the band only interacts with 10% of the outgoing infra-red radiation, this amounts to a total net increase of only 0.076% of all radiation being reflected.

3) This increase in reflection is only sufficient to raise global temperatures by 0.06°C.

NOTE: The above analysis assumes a scattering cross-section of σ_s = 1.6 x 10^-24 m². This unfortunately is just an estimate, and the true value could be up to an order of magnitude greater. Given the importance of this value to the whole theory of climate change one might think its value would be easily found and widely known, but unfortunately it is not. If σ_s is indeed greater by a factor of ten, then both Λ and the temperature increase due to the CO₂ concentration rising from 280 ppm to 420 ppm will be a factor of ten smaller.

87. How the Greenhouse Effect on Earth changes with increasing carbon dioxide concentration

In my previous post (Post 86) I explained how infra-red photons emitted by the Earth's surface interact with carbon dioxide (CO₂) in the atmosphere to create the Greenhouse Effect. I also showed that increasing the temperature of the planet and increasing the concentration of carbon dioxide in the atmosphere will both lead to an increase in the width of the 15 µm absorption band of CO₂. This in turn will increase the amount of radiation that is backscattered by the CO₂, and therefore increase the amount of radiation heating the surface of the planet. 

In this post I will attempt to quantify the temperature increase for different increases in the CO₂ content of the atmosphere using the results presented in Post 86 and Post 85. What I will show is that the increase in atmospheric levels of CO₂ from 280 ppm in 1750 to almost 420 ppm today can only be responsible for at most a 0.5°C increase in average temperatures. This is only about 40% of the 1.2°C claimed by the IPCC and climate scientists. In fact the actual temperature rise due to CO₂ is likely to be less than half the calculated value of 0.5°C due to the masking effects of water vapour, and could be as little as 0.1°C. To put this into context, this is less than the values I have calculated for urban heating effects from waste heat (see Post 14 and Post 29) which would persist even without the use of fossil fuels.

The maths and physics

The starting point for this analysis is the quantum structure of the absorption band. This is shown in Fig. 87.1 below and was discussed in detail in Post 86. The key issue is the height of the various absorption lines in the P and R branches. These are identified by their angular momentum quantum number, J, which is numbered for each branch from the centre of the band, Q. 

Fig. 87.1: The detailed structure of the 15 µm absorption band for CO₂ showing the absorption peaks associated with rotational transitions.

In Post 86 I also showed that the width of the 15 µm band is determined by the value of J that satisfies the following equation (see also Eq.86.9), this value being denoted as J_th.

(87.1)

In this equation T is the thermodynamic temperature in kelvins, k is the Boltzmann constant, h is Planck's constant and B is the frequency of the rotational angular momentum states. For the rotational transitions shown for CO₂ in Fig. 87.1, hB = 0.1 meV and is equal to half the energy separation of the lines in the spectrum in Fig. 87.1. The other terms will be explained below.

 

The Z term

The term Z is a normalization term equal to the total number of possible rotational states per molecule in the R (or P) branch as follows. 

(87.2)

 

In the case of Earth where the mean surface temperature T = 289 K, the term Z = 249.3. The energy term E_J = J(J+1)hB. As the degeneracy term (2J + 1) is the differential of the J component of the energy term J(J+1), it follows that for large T the summation in Eq. 87.2 reduces to an integral over all J states, in which case Z ≈ kT/hB.

 

 

The N_o term

 

The term N_o in Eq. 87.1 is equal to the total number of CO₂ molecules per unit surface area found in the R branch. This can be estimated as being equal to approximately half the molecules, with the other half being in the P branch which is assumed to be the mirror image of the R branch (but is not really as was explained in Post 86). This also neglects the significant number of CO₂ molecules (particularly at low temperatures) found in the Q peak. Nevertheless, this approach does at least set an upper limit to the width of the R branch, and thus the width of the 15 µm band as a whole. And as will be shown below, it does give results that are remarkably accurate. As the number of CO₂ molecules per unit surface area found on Earth is 150 moles per square metre, it therefore follows that N_o is equal to 75 mol/m².

Calculating N_th and J_th.

The final remaining parameter to calculate is N_th. Ideally, if the absorption band edge had vertical edges, it would be the threshold number of CO₂ molecules per unit area that are just sufficient to completely block the radiation and would be equal to the reciprocal of the scattering cross-section, σ_s. As σ_s for CO₂ molecules is estimated to be between 10^-24 m² and 10^-23 m² in the 15 µm band, that would imply a value for N_th of about 1 mol/m². In practice, however, the band edge is curved so the usual definition of the edge is to take the position of the half maximum. This means using a value of N_th = 0.5 mol/m² is more appropriate.

With all the parameters now set we can calculate J_th using Eq. 87.1 above. The result we get is 29.4, which when multiplied by the line spacing, 2hB, gives the width of the R branch as 47.4 cm^-1 in wavenumbers. Assuming the P branch is identical means that the 15 µm band will extend from 619.6 cm^-1 to 714.4 cm^-1, or from 14.00 µm to 16.14 µm. This is remarkably close to the 14.2 µm to 16.2 µm that is generally observed for the peak in the absorption.

Having calculated the width of the 15 µm band with an atmospheric CO₂ concentration of 420 ppm, we can also repeat the procedure for any other CO₂ concentration of our choosing. For example, an atmospheric CO₂ concentration of 280 ppm that is characteristic of global conditions in 1750 leads to a value for J_th of 27.3, which means that the width of the R branch would be 44.0 cm^-1.

The temperature rise

In Post 85 I showed how the reflection of a fraction f of outgoing infra-red radiation would reheat the Earth's surface and cause the radiation it absorbed to increase from I_o to a higher value I_T as follows

(87.3)

Then in Post 86 I showed how the width of the 15 µm absorption band could be used to determine the value of f by calculating the relative area of this band under the absorption spectrum (see Fig. 86.1). This can then be used to infer a temperature rise due to the absorption by utilizing the Stefan-Boltzmann law,

 I = σT⁴. 

(87.4)

If I_T is the intensity of radiation emitted by the Earth's surface normally (i.e. 396 W/m²), and f is the fraction of radiation reflected back by the CO₂, then the intensity of radiation emitted by the Earth's surface without the CO₂ greenhouse effect will, according to Eq. 87.3, be I_o = (1-f)I_T. We can then use Eq. 87.4 to calculate the respective surface temperatures T_f and T_o for each radiation emission intensity, I_T and I_o. The difference in the two temperatures will be the warming due to the CO₂.

I showed above that an atmospheric CO₂ concentration of 420 ppm leads to an absorption band that extends from 14.00 µm to 16.14 µm. Combining this with the black body spectrum of the Earth at T_f = 289 K (see Fig. 87.2 below) allows us to determine f to be f = 10.0%. This in turn implies that I_o = 356.1 W/m² (where I_o is the radiation intensity without CO₂ feedback), and thus T_o = 281.52 K. So the temperature rise due to CO₂ is 7.48 K.

 

Fig. 87.2: The electromagnetic emission spectrum for the Earth's surface at a mean temperature of 289K (blue curve) together with the absorption profile due to CO₂ between 14.00 µm and 16.14 µm (red curve).

Now if we reverse this calculation but use an atmospheric CO₂ concentration of 280 ppm, we find that the absorption band now extends from 14.06 µm to 16.05 µm, so f = 9.28%. The value of I_o = 356.1 W/m² will be the same as before but the addition of a different amount of CO₂ will change I_T and T_f because f is different. The new values will be I_T = 392.6 W/m² and T_f = 288.46 K. So the temperature rise from CO₂ is now only 6.94 K. This implies that the temperature rise since 1750 due to the atmospheric CO₂ concentration increasing from 280 ppm to 420 ppm is only 0.54°C (i.e. 7.48°C - 6.94°C). 

If we repeat this process for other past or future (potentially) CO₂ concentrations we can calculate a theoretical temperature rise for each. This is shown in the graph in Fig. 87.3 below with the temperature changes all measured relative to the 1750 value when the atmospheric CO₂ concentration was 280 ppm.

 

Fig. 87.3: The theoretical effect of an increasing atmospheric CO₂ concentration on the contribution of CO₂ to global warming.

What Fig. 87.3 demonstrates is that the expected temperature increase from an increase in atmospheric CO₂ has a logarithmic dependence on the CO₂ concentration. However, the trend for concentrations between 280 ppm and 420 ppm is fairly linear and leads to a 0.5°C increase. Overall it appears that doubling the CO₂ concentration leads to about 1°C (or 1 K) of warming.

The interpretation of the data

While the logarithmic trend shown in Fig. 87.3 is in general agreement with climate models, the magnitude of the temperature changes are not. Whereas Fig. 87.3 suggests that 420 ppm of CO₂ leads to about 0.52°C of warming, the IPCC and climate science are claiming the rise is much greater at about 1.2°C. The difference, I suspect, is probably down to the impact of water vapour. Unfortunately, there are many ways that water vapour can impact the temperature trend.

The conventional view from climate scientists is that water vapour is a positive amplifier; the theory being that a warmer climate causes the amount of water vapour in the troposphere to increase, thus creating even more warming. As I pointed out in Post 86, the total feedback factor for infra-red radiation, f, is about 59%, while CO₂ alone can only account for about 18%, assuming that the 15 µm CO₂ absorption band width is measured at its half-maximum points from 13.35 µm to 17.35 µm. So the assumption is that water vapour is responsible for the rest, and that as its atmospheric concentration is dependent on the temperature, its concentration will increase as the level of CO₂ increases. So this will make the feedback, f, increase about three times faster than from CO₂ alone and so massively increase the temperature change to 1.2°C. The problem with this theory is that it ignores two major snags. 

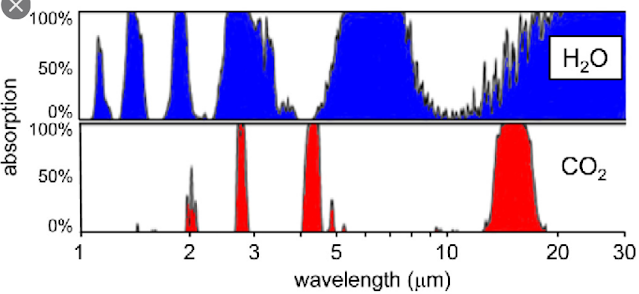
First, the 15 µm CO₂ absorption band overlaps with the H₂O absorption band, as shown in Fig. 87.4 below. At the high wavelength edge of the 15 µm CO₂ band (17 µm) the water vapour will absorb almost 100% of the outgoing radiation while at the low wavelength edge (13 µm) it will absorb about 50%. This means that about 75% of any increase in the width of the 15 µm CO₂ absorption band will be masked from the outgoing radiation by the water vapour. In which case the temperature rise will only be 25% of the predicted value, or about 0.13°C.

 

Fig. 87.4: The absorption bands of carbon dioxide and water vapour at sea level.

Secondly, the window in the H₂O absorption band extends from 8 µm to about 15 µm (using the half maxima points). This window allows only 41% of the Earth's outgoing infra-red radiation to escape. As we know that the feedback factor f = 59%, this means that water vapour could be responsible for absorbing and reflecting almost all the outgoing infra-red radiation that is absorbed and reflected. In other words, the 15 µm CO₂ band is not needed, and in fact is probably, largely redundant because it is hiding behind the water vapour. So again, a small change to the width of the CO₂ band is unlikely to cause any major temperature changes. This is why so many eminent physicists have so many serious reservations regarding the global warming predictions coming out of climate science.

 

The conclusions

1) Increasing the atmospheric CO₂ concentration will increase the width of its 15 µm absorption band.

2) In the absence of water vapour this could raise global temperatures, with an increase in CO₂ concentration from 280 ppm to 420 ppm resulting in a 0.5°C increase in global temperatures. 

3) The projected temperature increase has a logarithmic dependence on CO₂ concentration (see Fig. 87.3).

4) Water vapour masks most of the CO₂ 15 µm absorption band and so dominates the infra-red absorption. It can also account for almost all of the radiation feedback on its own.

5) The impact of water vapour means that an atmospheric CO₂ concentration rising from 280 ppm to 420 ppm could result in as little as a 0.13°C increase in global temperatures. This is ten times less than is currently claimed by climate science.

The caveats and discrepancies

In this analysis there are major uncertainties over the value of the CO₂ scattering cross-section, σ_s, and the widths of the CO₂ and H₂O absorption bands. This is also due to the difficulty in estimating the parameters N_o, N_th and J_th. However, the overall level of agreement between this analysis and real data and existing theory is encouraging.

The major discrepancy is between the measured width of the CO₂ 15 µm absorption band at its half maximum, where it extends from 13.35 µm to 17.35 µm, with the predicted width based on J_th where it extends from 14.00 µm to 16.14 µm. This difference could be due to line broadening from pressure broadening and temperature.