In this post I will consider a different impact of an increase to the atmospheric concentration of CO2 by calculating the strength of the backscattering at the centre of the 15 µm absorption band. This will involve describing the mathematical and statistical basis for the Greenhouse Effect, and how it arises from the backscattering of photons by greenhouse gas molecules. As a result I will show just how little infra-red radiation within the 15 µm band can escape through the atmosphere, and so also show just how insensitive the backscattering and transmission of infra-red radiation are to further increases in the CO2 concentration. Finally, I will calculate the expected temperature change for an increase in atmospheric CO2 concentrations from 280 ppm to 420 ppm, and show that it is significantly less than 0.1°C.
How the scattering process works
The origin of the Greenhouse Effect is the interaction of infra-red photons with air molecules, specifically those of carbon dioxide (CO2) and water vapour (H2O). While all air molecules, including those of both oxygen and nitrogen, are capable of scattering infra-red photons via the process of Rayleigh scattering, this scattering is so weak at infra-red wavelengths that it is unimportant. In fact in Post 86 I showed that Rayleigh scattering at wavelengths of 15 µm is a million times weaker than that seen for visible light and which gives the daytime sky its blue colour.
Instead, the dominant process is one of absorption and re-emission of photons where air molecules absorb radiation, and then re-emit it in a random direction. This is only important at wavelengths that match both the peak in the thermal emission spectrum of the Earth's surface (from about 5 µm to 100 µm) and the excitation energies of the molecules. As only CO2 and H2O of the main components of the atmosphere have excitation energies that match the peak region of the thermal emission spectrum of the Earth's surface, they are the most important greenhouse gases.
As I showed in Post 86, the combined absorption and re-emission process results in radiation received from one direction (i.e. the Earth's surface) being redistributed in all directions with equal probability. This is because the time delay between absorption and re-emission means that the orientation of the emitting molecules could be in any random direction. The result is a process that looks just like random scattering, and because the direction of scattering is random it is determined by statistical probability.
One way to visualize the backscattering process is by considering the photons of outgoing infra-red radiation as particles that, every so often, collide with greenhouse gas molecules, and bounce off them at random angles. We can define the average distance photons travel between these collisions as the mean free path. At each collision half the phonons will be reflected back in the opposite direction from which they came, while the other half will be scattered forward. But eventually those that are scattered forward will collide with another molecule and half of those will also be backscattered. This process continues as the remaining forward scattered photons travel further into the medium or gas with more and more being reflected. The result is that, eventually almost all the photons have been reflected back, and virtually none are travelling in the original forward direction. This is how the backscattering process works.
It is important to acknowledge, however, that the real process that is occurring is not a backscattering one. The infra-red photons are actually being absorbed by CO2 molecules which then become excited. They may then transfer this energy to other air molecules via collisions, but eventually those other air molecules will transfer the energy back to the CO2 and the CO2 molecules will re-emit it in some random direction. The time this process takes could be quite long, or very short, but it is happening so often that it will appear almost instantaneous. And therefore it will look just like scattering.
The mathematics of scattering
In order to gauge the importance of this process we need to quantify it. That means defining the process mathematically. By doing so we will be able to see which factors affect the amount of backscattering, and in particular, how it depends on the thickness of the atmosphere and its CO2 concentration.
In order to do this we must first construct a model of the atmosphere and consider a thin horizontal layer of the atmosphere of thickness δx at some arbitrary altitude x as shown in Fig. 88.1 below. In this model the density of carbon dioxide molecules is n(x), the intensity of the upwelling (or outgoing) radiation at a height x is Iu(x), and the intensity of the downwelling (or backscattered) radiation at the same height is Id(x).
In thermal equilibrium the atmosphere will emit the same number of photons each second that it absorbs. This is the origin of the scattering process. Conservation of energy then dictates that the difference between Iu(x) and Id(x) must be the same at all heights, x, and equal to the total intensity transmitted at the top of the atmosphere. It therefore follows that
Iu(x) - Id(x) = IoΛ
(88.1)
where Λ is the effective total transmission coefficient of the atmosphere and Io = Iu(0) is the total intensity of radiation emitted at the surface.
Now we consider the change in intensities of Iu(x) and Id(x) as the radiation passes through the thin layer of thickness δx at height x (see Fig. 88.1 above). In each case there is a probability δp that each photon will be scattered where
δp = n(x)σsδx
(88.2)
and σs is the scattering (or absorption) cross-section of the CO2 molecule at the particular wavelength of the radiation being considered. For each photon that is scattered, half will be scattered forwards and half will be scattered backwards. This means that the value of Iu(x) will decrease by ½Iu(x)δp but increase by ½Id(x)δp due to the backscattering of the reflected photons in Id(x). For Id(x) the opposite will be true. It therefore follows that the change in Iu(x) for a positive increase in x of δx will be
δIu(x) = ½[Id(x) - Iu(x)]n(x)σsδx
(88.3)
while the change in Id(x) for a positive increase in x of δx will be (note the extra negative sign)
δId(x) = -½[Iu(x) - Id(x)]n(x)σsδx
(88.4)
These results can be written in differential form as
The solution to Eq. 88.5 will depend on the distribution of the CO2 molecules within the atmosphere, n(x), and the boundary conditions. The first boundary condition is Iu(0) = Io and sets the amount of radiation that initially enters the atmosphere from the surface. The second is Id(h) = 0 where h is the height of the atmosphere, and this states that once the radiation leaves the top of the atmosphere there can be no more backscattering. The final piece of information we need is the dependence of the CO2 concentration on altitude, n(x).
The simplest model is to assume n(x) is constant (and equal to no) and thus independent of x. This is a fairly good approximation for the lower part of the troposphere and it is one I shall use as a starting point for the analysis.
Transmission coefficient for a gas of uniform density
From Eq. 88.1 we can see that Iu(x) - Id(x) must be a constant. As n(x) is a constant, Eq. 88.5 dictates that the first differentials of both Iu(x) and Id(x) must be constant as well. It therefore follows that
The solution for Id(x) must then be of the form Id(x) = a(h - x) to satisfy both Eq. 88.6 and the boundary condition Id(h) = 0, while Eq. 88.5 demands that a = ½ΛIonoσs. So
Id(x) = ½ΛIonoσs(h - x)
(88.7)
The only unknown term is Λ, but we can determine it from Eq. 88.1 and the boundary condition for Iu(0) = Io.
From Eq. 88.1 we see that Iu(x) = a(h - x) + IoΛ, which means that at x = 0 the condition Io = ah + IoΛ must hold. This means that the fraction of radiation that is transmitted at the top of the atmosphere, Λ, is given by
If noσsh >> 2, then Λ ≈ 2/noσsh.
It also means that Iu(x) will have a negative linear dependence on x when x < h as follows
while for x > h we find that the transmitted intensity is Iu(x) = IoΛ. This negative linear dependence is very different from the exponential decay that is usually associated with pure absorption or attenuation of radiation and described by the Beer-Lambert law.
Knowing Λ allows us to estimate the percentage of infra-red radiation within the 15 µm absorption band that escapes through the atmosphere for different CO2 concentrations, no. A CO2 concentration of 280 ppm (as existed before 1750) equates to a CO2 molecular concentration of no = 0.0118 mol/m3. The effective thickness of the atmosphere (h) at uniform density is approximately 10 km, while the scattering cross-section (σs) was estimated at around 1.6 x 10-24 m2 in Post 87. This gives a value for Λ of 1.67%. But if we instead consider a CO2 concentration of 420 ppm (as exists today), no = 0.0177 mol/m3 and Λ = 1.12%. So an increase in the CO2 concentration from 280 ppm to 420 ppm leads to the proportion of radiation being reflected by the 15µm CO2 absorption band increasing from 98.33% to 98.88%. This will lead to a (small) increase in the surface temperature which we can now estimate.
In Post 86 I showed that the width of the 15 µm band typically extends from about 13.35 µm to 17.35 µm and thus reflects about 18.1% of all the infra-red radiation emitted by the Earth's surface. But that assumes that the reflectivity of the band is 100%. In fact it is only 98.88%, having risen from 98.33% due to the increase in atmospheric CO2. This means that the increase in CO2 will, in effect, have caused the feedback factor, f, to rise from 18.0% to its current value of 18.1%. We can then use this information, together with the Stefan-Boltzmann law, to determine the change in the surface temperature as we know that 1-f is inversely proportional to T4. What we find is that the temperature rise associated with this increase in reflectivity (and hence increase in f) is less than 0.09°C. In fact the actual rise will be probably be less than half this value due to the masking effect of the water vapour.
Result: Increasing the CO2 concentration from 280 ppm to 420 ppm results in a global temperature increase of less than 0.09°C.
Transmission coefficient for a real atmosphere
The analysis so far has assumed that the atmosphere has a finite thickness of constant density that is independent of altitude. This, though, is not true for Earth. The increasing gravitational potential energy with increasing altitude means that fewer molecules have sufficient energy to reach high altitudes. The result is that the density of air decreases with height, and that dependence on height is exponential.
As carbon dioxide molecules are about 50% heavier than those of oxygen and nitrogen one might expect even fewer CO2 molecules to be present by percentage at high altitudes, but this is not the case. The mixing ratio does not appear to change significantly with altitude. So if there are 420 molecules of CO2 in every one million molecules of air at sea level, the same is true at heights of 10 km, 25 km, and 50 km. It is just that there are fewer numbers of all molecules at those altitudes.
Over the bottom 80 km of the atmosphere the molecular density, n(x), varies with altitude (x) as
n(x) = no e-kx
(88.10)
where k = 1.4 x 10-4 m-1. The same dependence is seen for CO2 with no = 0.0177 mol/m3 for an atmosphere containing 420 ppm of CO2, and no = 0.0118 mol/m3 for an atmosphere containing 280 ppm of CO2. The dependence of molecular density on altitude changes some of the mathematics outlined in the previous section, but both Eq. 88.1 and Eq. 88.5 will remain unaffected. The first change is to substitute Eq. 88.10 into Eq. 88.5 to give
(88.11)
It therefore follows that Iu(x) is given by
(88.12)
where c is a constant of integration. In which case Id(x) will be
(88.13)
The values of c and Λ will be dictated by the boundary conditions, Iu(0) = Io and Id(h) = 0, which are the same as before. Consequently, the results for c and Λ are
(88.14)
and
(88.15)
It can be seen that if kh << 1, then Eq. 88.15 reduces to the same approximate form as Eq. 88.8, and so both the reflectivity and the temperature rise will be the same as before (see previous section). The more realistic scenario, though, is for kh >> 1, particularly if h > 80 km (in which case kh = 11.2). Then Eq. 88.15 reduces to
(88.16)
which if noσs >> 2k, then becomes Λ ≈ 2k/noσs. We can now calculate the expected temperature rise by following a similar procedure to that outlined at the end of the previous section.
If no = 0.0118 mol/m3 (equivalent to a CO2 concentration of 280 ppm), then Λ = 0.0232 and so 97.68% of the radiation at 15 µm is being absorbed and then reflected. However, if no = 0.0177 mol/m3 (equivalent to a CO2 concentration of 420 ppm), then Λ = 0.0156. This means that an increase in the CO2 concentration from 280 ppm to 420 ppm leads to the proportion of radiation being reflected by the 15µm CO2 absorption band increasing from 97.68% to 98.44%. Given that the feedback factor for the 15 µm band is currently f = 0.181, this suggests that the previous value was 0.1796.
As the current mean temperature is 289 K, and the temperature must have increased by a factor of [ (1 - 0.1796)/(1 - 0.181) ]1/4 due to the change in feedback factor, then the corresponding temperature rise must be only 0.12°C. Once again the masking effect of absorption by water vapour in the same frequency range as CO2 will probably halve the real value of f from CO2 . So a large increase in the CO2 concentration will probably have less than half the effect on the mean global temperature than is stated here.
Result: Increasing the CO2 concentration from 280 ppm to 420 ppm results in a global temperature increase of less than 0.12°C.
Conclusions
1) Increasing the atmospheric CO2 concentration from 280 ppm to 420 ppm results in the infra-red transmission through the 15 µm absorption band reducing from 2.32% to 1.56%.
2) This leads to the 15 µm band reflecting back an extra 0.76% of the radiation within the borders of the band. But as the band only interacts with 10% of the outgoing infra-red radiation, this amounts to a total net increase of only 0.076% of all radiation being reflected.
3) This increase in reflection is only sufficient to raise global temperatures by 0.06°C.
NOTE: The above analysis assumes a scattering cross-section of σs = 1.6 x 10-24 m2. This unfortunately is just an estimate, and the true value could be up to an order of magnitude greater. Given the importance of this value to the whole theory of climate change one might think its value would be easily found and widely known, but unfortunately it is not. If σs is indeed greater by a factor of ten, then both Λ and the temperature increase due to the CO2 concentration rising from 280 ppm to 420 ppm will be a factor of ten smaller.








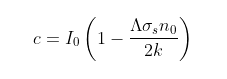


No comments:
Post a Comment