In my previous post (Post 85) I countered a number of myths surrounding the greenhouse effect, and outlined how it really works. Many people falsely believe that it is caused by a heating of the atmosphere by outgoing infra-red radiation, but this is not the case. The key concept at the heart of the greenhouse effect is photon scattering, or more accurately, the absorption and re-emission of infra-red photons by molecules of the greenhouse gases. There are three main gases that perform this role: carbon dioxide (CO2), water vapour (H2O), and methane (CH4). Each of these compounds absorbs electromagnetic radiation at its own set of unique wavelengths, but it is the absorption in the wavelength range between 6 µm and 90 µm that is key as this is where 96% of the thermal emission from the Earth's surface takes place. As CO2 is seen as the most important player in terms of anthropogenic greenhouse gas emissions I will consider its role in greatest detail.
The emission and absorption spectra
In Fig. 85.1 of Post 85 I showed the main absorption bands of carbon dioxide in the infra-red part of the electromagnetic spectrum. In total there are four main bands at 2 µm, 2.7 µm, 4 µm and 15 µm, but only the 15 µm band is of any importance as the other three have energies that are way beyond the peak of the infra-red emission spectrum for Earth's outgoing radiation. This is illustrated in Fig. 86.1 below, where the blue curve represents the Earth's emission spectrum at 289 K and the red curve shows which frequencies are absorbed by CO2. The area under the blue curve thus represents the total power of the radiation emitted at the Earth's surface, while the area under the red curve is the amount of radiated heat that can be absorbed and then reflected by CO2.
Fig. 86.1: The electromagnetic emission spectrum for the Earth's surface at a mean temperature of 289K (blue curve) together with the absorption profile due to CO2 between 14.2 µm and 16.2 µm (red curve).
The graph in Fig. 86.1 shows that only the 15 µm band is important as it is the only one close to the radiation peak. It is centred at 667 wavenumbers. Note: wavenumbers are the number of wavelengths of a radiation type that can fit in a distance of one centimetre. They are used because they are a measure of frequency, they result in much smaller numbers compared to other units of frequency like hertz, and are proportional to the photon energy of the radiation. The absorption bands at 2 µm, 2.7 µm and 4 µm correspond to wavenumbers of 5000, 3704 and 2500 cm-1 respectively. Consequently, they can only interact with the tail of the frequency spectrum where there is very little energy being emitted (i.e. less than 1% of the total).
What the curves in Fig. 86.1 show is that only about 9% of the Earth's outgoing radiation can be absorbed and then reflected back by the carbon dioxide molecules in the atmosphere. In other words, the area under the red curve is only 9% of the area under the blue curve. Yet in Post 85 I showed that in reality 59% of the radiation is reflected back. The difference in these two numbers is largely due to water vapour which not only accounts for most of that difference (i.e. 50%), but also overlaps the 15 µm absorption peak of CO2 (see Fig. 85.1 in Post 85), and so may render much of its function redundant. This is one reason why the claim that increasing the amount of CO2 in the atmosphere will necessarily increase the strength of the greenhouse effect is disputed by many.
Fig. 86.2: The absorption bands of carbon dioxide and water vapour at sea level.
The other complicating factor is the actual width of the 15 µm band. The peak of maximum absorption generally stretches from about 14.2 µm to 16.2 µm, or from about 700 to 620 wavenumbers (or a width of 10.8 meV), and results in a feedback factor f = 9.2% and a temperature rise of 6.88°C.
The band width, though, is dependent on both temperature and pressure. The full band at its tails can stretch from 12.5 µm to 18.5 µm (800 to 540 wavenumbers or a width of 32.2 meV), but absorption in the outer parts of the band decreases dramatically (see Fig. 86.2 above). If we were to use the full width of the band to determine the backscatter it would result in 26.8% of the outgoing radiation being reflected (see Fig. 86.3 below) and a temperature rise of 21.7°C; still much less than the 59% backscatter and the 58°C temperature rise that is actually seen.
Fig. 86.3: The electromagnetic emission spectrum for the Earth's surface at a mean temperature of 289K (blue curve) together with the potential absorption profile due to CO2 between 12.5 µm and 18.5 µm (red curve).
A more realist estimate would be achieved by considering the width at the half maximum points of the band. This will be from about 13.35 µm to 17.35 µm (749 to 576 wavenumbers or a width of 21.4 meV) and would result in an absorption and reflection of 18.1%. This equates to a temperature rise at the surface of the Earth of 14.1°C.
Backscattering by Rayleigh scattering
The photons of infra-red radiation emitted by the Earth's surface interact with the carbon dioxide in two ways. One is by elastic scattering and the other via absorption and re-emission.
In elastic scattering the photons basically bounce off the CO2 molecules like the collision of two billiard balls. This is the basis of what is known as Rayleigh scattering, named after the nineteenth-century British physicist Lord Rayleigh (John William Strutt), and it is a result of the electromagnetic interaction of the photon with the charged particles (electrons and protons) in the molecule. After collision the photons will end up travelling in a different direction. Some will be reflected back while others will carry on in a forward direction. It is the ones that are reflected that contribute to the greenhouse effect. The intensity of photons at a distance R from the molecule after being scattered through an angle θ is given by the equation
It can be seen that the overall scattering probability depends on the wavelength of the radiation (λ) and the strength of the polarizability of the molecule doing the scattering (α). The strong inverse dependence on wavelength explains why the sky is blue in daylight. This happens because blue light photons with wavelengths of about 400 nm scatter sixteen times more often as they travel through the Earth's atmosphere than red light photons of wavelength 800 nm do. It also means that Rayleigh scattering from carbon dioxide at wavelengths of 15 µm is about a billion times less likely to occur than the scattering of visible light. This is because the wavelengths of the photons being scattered are at least twenty times greater, so the scattering rate of 15 µm photons by CO2 molecules is at least 160,000 times less than for visible light. But in addition, the proportion of CO2 in the atmosphere is only 0.042% of all the molecules. This equates to about 150 moles of CO2 per square metre of the Earth's surface.
Another way of describing the strength of the scattering is via a scattering cross-section, σs. This is a measure of the effective cross-sectional area of each molecule that a photon will see, or alternatively how effective that molecule is at blocking the radiation. The scattering cross-section is usually (but not always) much less than the physical dimension of the molecule.
Using the definition of scattering cross-section Eq. 86.1 becomes
The key point, therefore, is that Rayleigh scattering is of negligible importance when discussing the greenhouse effect because it is a billion times weaker than the Rayleigh scattering we see of visible light. Absorption and re-emission of photons by the 15 µm band are the more important processes, but as I will explain next, their combined behaviour in terms of scattering is very similar to Rayleigh scattering, but much stronger.
Backscattering by absorption and re-emission
Almost all backscattering by carbon dioxide occurs via a process of absorption and re-emission of the infra-red photons with wavelengths in the region of the 15 µm band (i.e. 12.5-18.5 µm). The closer these photons are in wavelength to the centre of the band the more strongly they are absorbed.
Once excited, the molecule may then collide with other molecules and exchange its extra energy with them, thereby heating the gas as a whole. But once all the gas is heated equally, thermal equilibrium will be established where some of the excited CO2 molecules will re-emit photons at the same rate that other CO2 molecules are absorbing them. This situation physicists refer to as the steady state. At this point, for every photon being absorbed, another is being re-emitted by another molecule in a random direction.
Ultimately, every molecule wants to get to its lowest energy state, so while bombarding it with radiation will force its energy state to increase, it also increases the rate at which it tries to lose energy. So eventually an equilibrium is achieved where the amount of radiation being absorbed by the gas balances the amount that is lost through re-emission. The key point to note, though, is that the re-emission is a random process that can result in the emitted photons being ejected in any direction. In contrast, most of the absorbed photons come from a single direction: the Earth's surface. This means that fewer of the re-emitted photons end up travelling away from the surface as some are reflected back. Those photons that are reflected back then provide additional heat to the surface, thereby raising its temperature even further. This is the origin of the Greenhouse Effect.
Structure of the absorption band
The infra-red photons emitted from the Earth's surface are absorbed by carbon dioxide via a process of molecular excitation where the molecule is promoted to a higher energy state. Usually this process is in the form of electrons within the molecule moving to higher energy levels, but those transitions are usually of very high energy (several electron volts or eV) and so they only result from the absorption of visible or ultraviolet light.
The 15 µm transition in carbon dioxide is in the infra-red part of the spectrum and so it is of a much lower energy (about 83 meV). Instead it results from a bond stretching excitation where the molecule bends, as shown in mode v2 in Fig. 86.4 below, under the action of the incoming electromagnetic wave of the photon. This bond stretching occurs because of an uneven distribution of electric charge within the molecule which then interacts with the electric field of the incoming electromagnetic wave or photon.
In addition to the bond stretching, a much smaller amount of energy from the incoming photon may go towards increasing the angular momentum or rotational spin of the molecule. This leads to "wings" or branches to the central band as shown in Fig. 86.5 below, with the lower energy branch being denoted as the P branch, and the higher energy one the R branch. It is these branches that cause the band to broaden from a single sharp peak Q at 15 µm to a broader band stretching from 12.5 µm to 18.5 µm.
Fig. 86.5: The detailed structure of the 15 µm absorption band for CO2 showing the absorption peaks associated with rotational transitions.
The branches P and R are each comprised of a set of evenly spaced discrete transitions, each one matched to a different change in rotational energy of the molecule due to a change in its angular momentum state J by an amount ∆J = ±1. This is because the incoming photon has an angular momentum quantum of J = +1 and angular momentum must be conserved in the absorption process. The R branch arises from absorption processes where the photon causes the molecule to spin faster, while the P branch arises from absorption processes where the photon causes the molecule to spin more slowly (i.e. the angular momentum of the photon is in the opposite direction to that of the molecule). The two branches are, in theory, mirror images of each other, but in practice centrifugal distortion and rotational-vibrational coupling lead to the line spacing increasing at lower energies.
As the energy of each rotational state J of the molecule is (ideally) equal to J(J+1)hB where h is Planck's constant and B is given by
with I being the moment of inertia of the molecule about its spin axis, the energy change associated with a transition from state J to J+1 when a photon is absorbed will be ±2hB(J+1) (see here). So the absorption peaks due to changes in rotation have an ideal energy separation of 2hB, or about 1.54 wavenumbers (cm-1) or 0.2 meV for lines in the 15 µm band of carbon dioxide.
These individual line transitions are also broadened via doppler broadening due to the different speeds and directions of motion of the various molecules, and pressure broadening due to collisions with other molecules in the atmosphere. Both of these broadening mechanisms are temperature dependent and increase as the temperature increases. The result is that the width and overall scattering cross-section of each line will increase with temperature thereby narrowing or closing completely the gaps between the individual rotational lines in the spectrum. For lines in the 15 µm absorption band of CO2 the typical scattering cross-section is about 10-23 m2, which is about one trillion (i.e. 1012) times greater than the scattering cross-section of each molecule due to Rayleigh scattering at the same wavelength.
In addition, an increase in temperature will shift the position of the peak or maximum in both the P and R branches, Jmax (again see here). This is because the height of each line in the 15 µm band is dependent on both its J number and the temperature. Each line has a degeneracy of 2J+1, while the probability of exciting that rotational J mode depends exponentially on both energy and temperature. This means that the relative occupancy of each mode, NJ, is given by
where the energy EJ of the mode J is given by J(J+1)hB, No is the total number of excited modes, and Z is a normalization term that is equal to the sum of the probabilities.
This also explains why the P and R branches in Fig. 86.5 have peaks in their distributions. The occupancy of each rotational state NJ increases linearly with J via the degeneracy term 2J+1, but for large J decreases more rapidly due to the energy term EJ in the exponential. This leads to a maximum in the distribution, the position of which relative to the band centre at Q can be determined by differentiation with respect to J. The result is given by
What this shows is that as the temperature of the gas increases, the position of the maxima will move further from the band centre at Q, so the overall width of the band will increase with temperature as well. This is because higher temperatures will lead to a higher proportion of CO2 molecules in higher energy rotational states with larger J values. Generally, though, it takes a large temperature change to significantly widen the band. As the position of the R branch maximum relative to Q increases with temperature T as √T, it is reasonable to expect the width of the band to do the same.
Finally, if the width of the absorption band can change with temperature, then it can also change with CO2 concentration. In this case the width will be set by the highest value of J for which NJ exceeds some threshold value Nth, this being the number of modes required to almost completely absorb the outgoing radiation at that wavelength. According to Eq. 86.5 this will be the value of J such that
Rearranging Eq. 86.8 gives the following result for the threshold J value, Jth, that defines the edge of the band
So Eq. 86.9 not only confirms that the band width varies approximately as √T, but also that it varies approximately as √ln(No).
Conclusions
The dominant mechanism by which CO2 molecules scatter infra-red radiation in the 15 µm band is by absorption and re-emission.
The absorption and re-emission process has a similar effect to that of Rayleigh scattering, but it is almost a trillion (i.e. 1012) times stronger.
The width of the 15 µm band increases with temperature as √T, but increases much more slowly with CO2 concentration (see Eq. 86.9).




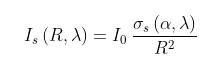









No comments:
Post a Comment