In my previous post (Post 86) I explained how infra-red photons emitted by the Earth's surface interact with carbon dioxide (CO2) in the atmosphere to create the Greenhouse Effect. I also showed that increasing the temperature of the planet and increasing the concentration of carbon dioxide in the atmosphere will both lead to an increase in the width of the 15 µm absorption band of CO2. This in turn will increase the amount of radiation that is backscattered by the CO2, and therefore increase the amount of radiation heating the surface of the planet.
In this post I will attempt to quantify the temperature increase for different increases in the CO2 content of the atmosphere using the results presented in Post 86 and Post 85. What I will show is that the increase in atmospheric levels of CO2 from 280 ppm in 1750 to almost 420 ppm today can only be responsible for at most a 0.5°C increase in average temperatures. This is only about 40% of the 1.2°C claimed by the IPCC and climate scientists. In fact the actual temperature rise due to CO2 is likely to be less than half the calculated value of 0.5°C due to the masking effects of water vapour, and could be as little as 0.1°C. To put this into context, this is less than the values I have calculated for urban heating effects from waste heat (see Post 14 and Post 29) which would persist even without the use of fossil fuels.
The maths and physics
The starting point for this analysis is the quantum structure of the absorption band. This is shown in Fig. 87.1 below and was discussed in detail in Post 86. The key issue is the height of the various absorption lines in the P and R branches. These are identified by their angular momentum quantum number, J, which is numbered for each branch from the centre of the band, Q.
Fig. 87.1: The detailed structure of the 15 µm absorption band for CO2 showing the absorption peaks associated with rotational transitions.
In Post 86 I also showed that the width of the 15 µm band is determined by the value of J that satisfies the following equation (see also Eq.86.9), this value being denoted as Jth.
In this equation T is the thermodynamic temperature in kelvins, k is the Boltzmann constant, h is Planck's constant and B is the frequency of the rotational angular momentum states. For the rotational transitions shown for CO2 in Fig. 87.1, hB = 0.1 meV and is equal to half the energy separation of the lines in the spectrum in Fig. 87.1. The other terms will be explained below.
The Z term
The term Z is a normalization term equal to the total number of possible rotational states per molecule in the R (or P) branch as follows.
Calculating Nth and Jth.
The final remaining parameter to calculate is Nth. Ideally, if the absorption band edge had vertical edges, it would be the threshold number of CO2 molecules per unit area that are just sufficient to completely block the radiation and would be equal to the reciprocal of the scattering cross-section, σs. As σs for CO2 molecules is estimated to be between 10-24 m2 and 10-23 m2 in the 15 µm band, that would imply a value for Nth of about 1 mol/m2. In practice, however, the band edge is curved so the usual definition of the edge is to take the position of the half maximum. This means using a value of Nth = 0.5 mol/m2 is more appropriate.
With all the parameters now set we can calculate Jth using Eq. 87.1 above. The result we get is 29.4, which when multiplied by the line spacing, 2hB, gives the width of the R branch as 47.4 cm-1 in wavenumbers. Assuming the P branch is identical means that the 15 µm band will extend from 619.6 cm-1 to 714.4 cm-1, or from 14.00 µm to 16.14 µm. This is remarkably close to the 14.2 µm to 16.2 µm that is generally observed for the peak in the absorption.
Having calculated the width of the 15 µm band with an atmospheric CO2 concentration of 420 ppm, we can also repeat the procedure for any other CO2 concentration of our choosing. For example, an atmospheric CO2 concentration of 280 ppm that is characteristic of global conditions in 1750 leads to a value for Jth of 27.3, which means that the width of the R branch would be 44.0 cm-1.
The temperature rise
In Post 85 I showed how the reflection of a fraction f of outgoing infra-red radiation would reheat the Earth's surface and cause the radiation it absorbed to increase from Io to a higher value IT as follows
Then in Post 86 I showed how the width of the 15 µm absorption band could be used to determine the value of f by calculating the relative area of this band under the absorption spectrum (see Fig. 86.1). This can then be used to infer a temperature rise due to the absorption by utilizing the Stefan-Boltzmann law,
I = σT4.
(87.4)
If IT is the intensity of radiation emitted by the Earth's surface normally (i.e. 396 W/m2), and f is the fraction of radiation reflected back by the CO2, then the intensity of radiation emitted by the Earth's surface without the CO2 greenhouse effect will, according to Eq. 87.3, be Io = (1-f)IT. We can then use Eq. 87.4 to calculate the respective surface temperatures Tf and To for each radiation emission intensity, IT and Io. The difference in the two temperatures will be the warming due to the CO2.
I showed above that an atmospheric CO2 concentration of 420 ppm leads to an absorption band that extends from 14.00 µm to 16.14 µm. Combining this with the black body spectrum of the Earth at Tf = 289 K (see Fig. 87.2 below) allows us to determine f to be f = 10.0%. This in turn implies that Io = 356.1 W/m2 (where Io is the radiation intensity without CO2 feedback), and thus To = 281.52 K. So the temperature rise due to CO2 is 7.48 K.
Now if we reverse this calculation but use an atmospheric CO2 concentration of 280 ppm, we find that the absorption band now extends from 14.06 µm to 16.05 µm, so f = 9.28%. The value of Io = 356.1 W/m2 will be the same as before but the addition of a different amount of CO2 will change IT and Tf because f is different. The new values will be IT = 392.6 W/m2 and Tf = 288.46 K. So the temperature rise from CO2 is now only 6.94 K. This implies that the temperature rise since 1750 due to the atmospheric CO2 concentration increasing from 280 ppm to 420 ppm is only 0.54°C (i.e. 7.48°C - 6.94°C).
If we repeat this process for other past or future (potentially) CO2 concentrations we can calculate a theoretical temperature rise for each. This is shown in the graph in Fig. 87.3 below with the temperature changes all measured relative to the 1750 value when the atmospheric CO2 concentration was 280 ppm.
What Fig. 87.3 demonstrates is that the expected temperature increase from an increase in atmospheric CO2 has a logarithmic dependence on the CO2 concentration. However, the trend for concentrations between 280 ppm and 420 ppm is fairly linear and leads to a 0.5°C increase. Overall it appears that doubling the CO2 concentration leads to about 1°C (or 1 K) of warming.
The interpretation of the data
While the logarithmic trend shown in Fig. 87.3 is in general agreement with climate models, the magnitude of the temperature changes are not. Whereas Fig. 87.3 suggests that 420 ppm of CO2 leads to about 0.52°C of warming, the IPCC and climate science are claiming the rise is much greater at about 1.2°C. The difference, I suspect, is probably down to the impact of water vapour. Unfortunately, there are many ways that water vapour can impact the temperature trend.
The conventional view from climate scientists is that water vapour is a positive amplifier; the theory being that a warmer climate causes the amount of water vapour in the troposphere to increase, thus creating even more warming. As I pointed out in Post 86, the total feedback factor for infra-red radiation, f, is about 59%, while CO2 alone can only account for about 18%, assuming that the 15 µm CO2 absorption band width is measured at its half-maximum points from 13.35 µm to 17.35 µm. So the assumption is that water vapour is responsible for the rest, and that as its atmospheric concentration is dependent on the temperature, its concentration will increase as the level of CO2 increases. So this will make the feedback, f, increase about three times faster than from CO2 alone and so massively increase the temperature change to 1.2°C. The problem with this theory is that it ignores two major snags.
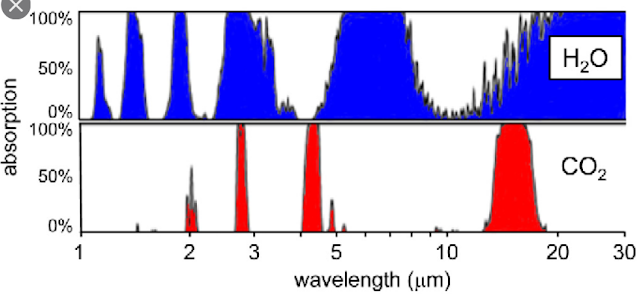
First, the 15 µm CO2 absorption band overlaps with the H2O absorption band, as shown in Fig. 87.4 below. At the high wavelength edge of the 15 µm CO2 band (17 µm) the water vapour will absorb almost 100% of the outgoing radiation while at the low wavelength edge (13 µm) it will absorb about 50%. This means that about 75% of any increase in the width of the 15 µm CO2 absorption band will be masked from the outgoing radiation by the water vapour. In which case the temperature rise will only be 25% of the predicted value, or about 0.13°C.
Secondly, the window in the H2O absorption band extends from 8 µm to about 15 µm (using the half maxima points). This window allows only 41% of the Earth's outgoing infra-red radiation to escape. As we know that the feedback factor f = 59%, this means that water vapour could be responsible for absorbing and reflecting almost all the outgoing infra-red radiation that is absorbed and reflected. In other words, the 15 µm CO2 band is not needed, and in fact is probably, largely redundant because it is hiding behind the water vapour. So again, a small change to the width of the CO2 band is unlikely to cause any major temperature changes. This is why so many eminent physicists have so many serious reservations regarding the global warming predictions coming out of climate science.
The conclusions
1) Increasing the atmospheric CO2 concentration will increase the width of its 15 µm absorption band.
2) In the absence of water vapour this could raise global temperatures, with an increase in CO2 concentration from 280 ppm to 420 ppm resulting in a 0.5°C increase in global temperatures.
3) The projected temperature increase has a logarithmic dependence on CO2 concentration (see Fig. 87.3).
4) Water vapour masks most of the CO2 15 µm absorption band and so dominates the infra-red absorption. It can also account for almost all of the radiation feedback on its own.
5) The impact of water vapour means that an atmospheric CO2 concentration rising from 280 ppm to 420 ppm could result in as little as a 0.13°C increase in global temperatures. This is ten times less than is currently claimed by climate science.
The caveats and discrepancies
In this analysis there are major uncertainties over the value of the CO2 scattering cross-section, σs, and the widths of the CO2 and H2O absorption bands. This is also due to the difficulty in estimating the parameters No, Nth and Jth. However, the overall level of agreement between this analysis and real data and existing theory is encouraging.
The major discrepancy is between the measured width of the CO2 15 µm absorption band at its half maximum, where it extends from 13.35 µm to 17.35 µm, with the predicted width based on Jth where it extends from 14.00 µm to 16.14 µm. This difference could be due to line broadening from pressure broadening and temperature.


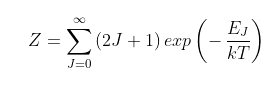


No comments:
Post a Comment