143: England - temperature trends WARMING

It is probably not surprising that England has more weather stations of note than Scotland. After all it has about ten times the population and almost twice the area. Yet the difference is not as great as one might imagine. For while Scotland has nine long stations with over 1200 months of data before 2014, England has only a slight advantage with ten stations. For medium stations with over 480 months of data the difference is greater with England having 55 compared to 13 in Scotland. There is, however, more clustering of stations in England as the map in Fig. 143.1 below shows.

Fig. 143.1: The (approximate) locations of the 65 longest weather station records in England. Those stations with a high warming trend between 1911 and 2010 are marked in red while those with a cooling or stable trend are marked in blue. Those denoted with squares are long stations with over 1200 months of data, while diamonds denote medium stations with more than 480 months of data.

In order to quantify the changes to the climate of England the temperature anomalies for all stations with over 480 months of data before 2014 were determined and averaged. This was done using the usual method as outlined in Post 47 and involved first calculating the temperature anomaly each month for each station relative to its monthly reference temperature (MRT), and then averaging those anomalies to determine the mean temperature anomaly (MTA) for the whole country for each month. The MRTs for England were calculated using the same 30-year period as for the UK in Post 141, namely from 1956-1985. 

The resulting MTA is shown as a time series in Fig. 143.2 below and clearly shows that temperatures rose slightly over 150 years up until 1975 before increasing more rapidly thereafter. In this respect the MTA data for England more resembles that of Great Britain (see Fig. 141.2 in Post 141) than it does that of Scotland (see Fig. 142.2 in Post 142) or Ireland (see Fig. 140.2 in Post 140).

Fig. 143.2: The mean temperature change for England since 1760 relative to the 1956-1985 monthly averages. The best fit is applied to the monthly mean data from 1826 to 1975 and has a positive gradient of +0.35 ± 0.08 °C per century.

The temperature trend for England was calculated using the usual method as outlined in Post 47 and involved first calculating the temperature anomaly each month for each station relative to its monthly reference temperature (MRT), and then averaging those anomalies to determine the mean temperature anomaly (MTA) for the whole country for each month. The graph in Fig. 143.3 below indicates how many stations were available each month in order to contribute to that month's MTA.

The MRTs for England were calculated using the same 30-year period as for the UK in Post 141, namely from 1956-1985. The resulting MTA is shown as a time series in Fig. 143.2 above and clearly shows that temperatures were slowly increasing for over 150 years up until 1975. Then at some point in the 1980s (probably in 1988) the mean temperature appears to increase abruptly by about 1°C. This is a phenomenon that has been seen in many other temperature trends across Europe.

Fig. 143.3: The number of station records included each month in the mean temperature anomaly (MTA) trend for England in Fig. 143.2.

If we next consider the change in temperature based on Berkeley Earth (BE) adjusted data we get the MTA data in Fig. 143.4 below. This again was determined by averaging each month the anomalies from the 65 longest stations and also suggests that the climate was warming slowly before 1980 but then warmed more strongly by over 1°C thereafter.

Fig. 143.4: Temperature trends for England based on Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1826-1975 and has a positive gradient of +0.27 ± 0.03°C/century.

The difference between the MTA based on raw unadjusted data (from Fig. 143.2) and the MTA based on BE adjusted data (from Fig. 143.4) is shown in Fig. 143.5 below. The blue curve in Fig. 143.5 is the difference in MTA values between the adjusted data (Fig. 143.4) and the unadjusted data (Fig. 143.2) and represents the total of all the data adjustments made including those from homogenization, gridding, Kriging and most significantly breakpoint adjustments. The orange curve is the contribution to those adjustments arising solely from breakpoint adjustments.

Fig. 143.5: The contribution of Berkeley Earth (BE) adjustments to the anomaly data in Fig. 143.4 after smoothing with a 12-month moving average. The blue curve represents the total BE adjustments including those from homogenization. The linear best fit (red line) to these adjustments for the period 1871-2010 has a small positive gradient of +0.003 ± 0.003 °C per century. The orange curve shows the contribution just from breakpoint adjustments.

The overall impact of any adjustments can perhaps be seen more clearly if we compare the 5-year averages for the raw unadjusted data and the BE adjusted data as is shown in Fig. 143.6 below. This shows that the two datasets agree almost perfectly from 1870 onwards while before 1870 the adjusted data implies the climate is more stable. It should be noted though that the MTA trends before 1870 are based on data from less than five stations and this drops to less than two before 1850 (see Fig. 143.3). This is one reason why the MTA exhibits more natural variability over the earlier period before 1870.

Fig. 143.6: The 5-year mean temperature change for England since 1760 based on the original raw data from Fig. 143.2 (in blue) and the Berkeley Earth adjusted data from Fig. 143.4 (in red).

Summary

What the raw data for England shows is that the climate was warming slowly for most of the period up to 1975 (see Fig. 143.2). This is similar to the trend seen previously for Great Britain (see Fig. 141.2 in Post 141), but is different from both Scotland (see Fig. 142.2 in Post 142) and Ireland (see Fig. 140.2 in Post 140) where little warming was seen in this period. This suggests that England is the dominant country in determining the overall climate of the UK but is also the outlier. But why?

The obvious answer is that England has a much greater population density and so experiences much more urban or surface heating from human activities (see Post 14, Post 29, Post 127 and Post 134). As I pointed out in Section (iv) of Post 127, the energy consumption of Greater London is sufficient to raise the local temperature by over 4°C.


Acronyms

BE = Berkeley Earth.

MRT = monthly reference temperature (see Post 47).

MTA = mean temperature anomaly.

Long station = a station with over 1200 months (100 years) of data before 2014.

Medium station = a station with over 480 months (40 years) of data before 2014.

134: Urban heat island (UHI) - implications for climate analysis

 

Fig. 134.1: UHI evidence from six cities in the Southern Hemisphere.

 

In my previous six posts I highlighted six examples of temperature records from major cities in the Southern Hemisphere where the temperature trend appears to be influenced by the urban heat island (UHI) effect that I discussed in Post 127. The result in each case was that the city exhibited significantly more warming than the rest of the state or country that the city was part of (see Fig. 134.1 above). However, the implications of this go beyond what is happening in a few megacities.

If large cities like Jakarta and Buenos Aires are warming because of urban heating, it then follows that smaller towns and cities must as well, only just not as much. As most weather stations are located near sites of human activity or habitation, it then also follows that most of the temperature records are likely to be corrupted to a certain degree by this UHI effect. The problem is determining to what degree that is. 

The six cities I have examined so far are obviously extreme examples and cannot on their own have a significant impact on their regional temperature trends as these regional trends are usually the result of averaging data from dozens of different stations. If they did have a large impact, then the difference between the trends for each city and its region would not be so pronounced. But that does not mean that the wider region is unaffected. 

The regional trends I compared each of the city trends with are also probably affected by the UHI effect, just not as much. That is because most of the data that goes to make up the regional trends comes from stations sited around other, smaller urban developments. So the regional warming is probably overstated as well, just not as much as that of the megacities. It is only because the megacities are so extreme that they stand out from their wider regions, but in reality both trends are likely to exhibit increased warming due to the UHI effect, just not as much as each other, hence the divergence in trends. 

And of course, if the temperature data for all the stations in the region is homogenized, then there is a risk of importing warming trends from the UHI into the surrounding area thereby raising the temperature trends of the wider region more markedly. Either way, the temperature trend for any region is likely to be corrupted to some degree by UHI effects in some of its stations.

But perhaps the biggest issue is the problem of area weighting. Ideally the contribution of each station to the overall regional average should be in proportion to area surrounding that station. So if a country has fifty stations and they are all evenly spaced, then each one should represent 2% of the area and each should make a 2% contribution to the mean temperature for the country. But suppose the station sits in a UHI and the area of the urban region is less than the nominal area that the station is supposed to represent. This is what happens with Jakarta in Indonesia (see Post 131) and for many other UHI stations.

The area of Jakarta is about 660 km², but that is only about 0.035% of the 1,900,000 km² area of Indonesia so the true weighting or contribution of Jakarta Observatorium (Berkeley Earth ID: 155660) to the mean temperature trend of Indonesia should be only 0.035%. But as there are less than sixty reliable temperature records for Indonesia (see Fig. 31.4 in Post 31) that means that each station on average makes a contribution of over 1.7% to the regional temperature trend. So a simple average of all station anomalies would over-represent Jakarta Observatorium (Berkeley Earth ID: 155660) by at least fifty times, and so too would an average based on a gridded method.

So how could we separate the UHI contribution to local warming from other climate drivers like carbon dioxide? One way to go about this might be to compare temperature trends for raw unadjusted temperature data from known urban and rural stations. But the problem here is that we don't know for certain where all these stations are exactly, or what the local geography around each station is. For example, according to its GPS coordinates Perth Regional Office is in the middle of the sea over 8 km off the coast of Perth. This is because the longitude and latitude coordinates for many stations are often only specified to the nearest 0.1° and sometimes the error is even greater. For Perth Regional Office the error is stated as ±0.2° for the longitude. That means its location accuracy is about ± 10 km. That is bigger than the extent of most urban areas. So finding sufficient pure rural stations against which to compare all the others is tough.

The takeaway here is that the urban heat island (UHI) effect is a big problem when interpreting temperature data, but determining how big is also a big problem.

127: The urban heat island (UHI) effect - an explainer

 

The urban heat island (UHI) effect.

 

The conventional wisdom is that climate change is driven by rising carbon dioxide (CO₂) levels in the atmosphere, and only by CO₂; so the greater the (CO₂) levels the greater the temperature increase (see Fig. 87.3 in Post 87). You may have noticed one direct consequence of this orthodoxy in the way the media these days reports on environmental disasters or extreme weather (floods, droughts, storms, hurricanes, heatwaves, forest fires etc.): they always refer to climate change.

Implicit to this climate change reference is the assumption that all climate change is due to CO₂ even though CO₂ is rarely explicitly mentioned and the causation is rarely demonstrated. Consequently, the solution to all extreme weather events appears to be simple and obvious: cut CO₂ levels in the atmosphere (i.e. Net Zero) and everything will be fine. Except it won't. This is because much of what is happening to local climates has little or nothing to do with CO₂, but it does have a lot to do with other human activities, not least urbanization and industrialization. Central to both of these is the urban heat island (UHI) effect.

The problem when discussing the impact of the UHI effect on climate, and in particular the temperature record, is that it is controversial. This is partly because much of climate science appears to be driven by an anti-fossil fuel dogma that therefore sees any talk of UHIs as at best a distraction from the supposed only true problem, CO₂, and at worst a campaign of disinformation designed to undermine all of climate science and its campaign against CO₂. But it is also partly because UHIs come in many flavours. 

There are those UHIs that just trap more heat by reducing airflows and those that store more solar heat than rural areas by virtue of increased heat capacities. Both of these do not add to the total amount of energy absorbed at the Earth's surface though, so there is no net global temperature increase associated with them. But then there are those UHI processes that do absorb extra heat, either via changes to the albedo of the Earth's surface, or by the emission of large amounts of additional heat through anthropogenic energy use and generation. Both of these certainly do add to global warming but are still largely ignored by climate science. In the following sections I will discuss the relative impact of each of these four types of UHI effect in turn and show that one type in particular can be very significant.

i) Heat trapping

The aspect of the UHI effect that is referred to the most is heat trapping. This is where tall buildings in a city reduce the flow of hot air away from the centre causing the city to retain its heat longer. Perhaps the most obvious example of this is Manhattan in New York City with its dense cluster of tall skyscrapers.

The result of this UHI effect is that the local area of the city stays hotter for longer compared to if the buildings were not there. This is because there is less diffusion of heat to outlying areas, so those areas are less likely to be warmed by the city and the city is less likely to be cooled by heat transfer to the rural areas that surround it. 

However, this does not lead to more global warming because while the city will be hotter for longer than otherwise expected, the surrounding area will be cooler for longer as well because less heat from the urban areas reaches the rural areas. The key point here is that no extra heat is created at the surface of the Earth, it is just prevented from diffusing to colder regions. So the net effect on local mean temperatures is zero. As an example consider the Grand Canyon. It will trap heat in the same way that tall buildings do, but does that mean that it is warming faster than the rest of Arizona? No, and nor does it make Arizona as a whole get any warmer.

This is one reason why climate scientists discount the UHI effect, and in this case they are right, provided that the weather stations used to monitor temperature changes are evenly distributed and their temperature readings are not adjusted. Those, unfortunately, are big IFs, because any bias in station numbers between urban and rural regions compared to their relative areas will affect the the relative contribution of each to the mean global temperature, and we do know that station densities are generally higher in urban areas. So potentially there are more warm urban stations contributing to the global average than there should be and fewer cold rural ones. In an ideal world, though, this should not occur, and so neither would any contribution to global temperatures.

Net effect on global warming: zero.

ii) Increased heat capacity

Probably the second most cited variation of the UHI effect is heat retention where cities heat up and store energy from the Sun during the day and then gradually release it overnight. The net effect of this is that the maximum temperature in the city during the day should be less than expected because of the time it takes the buildings to heat up. This is because the Sun is not just heating up the top layer of the Earth's surface, as would be the case in rural areas; it is also having to heat up large concrete structures with much higher heat capacities. The higher the local heat capacity of these structures, the longer it takes to warm them and the slower, and therefore lower, their temperature rise will be. This in turn means that less infra-red radiation is then radiated back into outer space during the day because the region is cooler than it would be without the buildings, and so there is less heating of the lower atmosphere and less downwelling radiation.

At night, however, the heating from the Sun stops. The rural areas cool quickly but the urban areas don't because the urban areas have the much higher heat capacity: there is more heat stored that needs to be lost before a new thermal equilibrium without the Sun can be established. So the buildings are now warmer than their rural surroundings but are slowly cooling, acting like large radiators or storage heaters. This means that the city stays warmer for longer, and temperatures within the city are higher at night than they would otherwise be. 

The net effect of this is that temperatures during the day will be lower, but those at night-time will be higher. Overall, though, the effect on the average temperature will be zero as the two changes in temperature cancel due to the fact that the changes in heat absorption will also cancel.

Net effect on global warming: zero.

iii) Increased heat absorption

One consequence of urban development is that it changes the reflectivity of the Earth's surface for incident visible, ultraviolet and near infra-red radiation. This reflectivity is known as the albedo and it is loosely related to the colour of a surface: darker colours tend to absorb more radiation while lighter ones generally reflect more. If the albedo increases, then more radiation is reflected back into space without heating the planet, so ice and snow help to cool the planet (their albedo is over 80%) while dark soil and oceans tend to warm the planet (see Table 14.1 in Post 14 for a list of typical albedos). It therefore follows that if the colour of a surface changes, then so will its albedo, and this can then change the amount of radiation absorbed at the surface. If this absorbed radiation increases, then the Earth will get warmer and the UHI effect is one way this can happen.

In Post 14 I explained that of the average incoming solar radiation of 341 W/m² that the Earth receives, only 161 W/m² is absorbed at its surface, and that greenhouse gases then amplify this with 333 W/m² of additional downwelling radiation. This total absorbed heat of 494 W/m² then dictates the mean surface temperature via the Stefan-Boltzmann law (see Post 12). It therefore follows that if any change occurs at the Earth's surface that increases the 161 W/m² of absorbed radiation, then this will change the downwelling radiation by the same percentage and therefore change the mean surface temperature as well.

The process of urbanization inevitably involves changing the colour and texture of the Earth's surface. It generally means that areas of vegetation are replaced with tarmac and concrete. Buildings with dark roofs absorb more solar radiation than trees and grassland. However the situation is not straightforward because concrete can be very reflective and arable land tends to be very dark. Overall though, there is generally a small decrease in albedo with urbanization, and therefore a small increase in the amount of solar radiation that is absorbed. This will raise the surface temperature of the Earth slightly as well, but because it is small it is not likely to be significant.

One human innovation that can have a big impact on temperature is solar power. Because solar panels are designed to absorb 99% of solar radiation, they will add additional heating to any area where they are installed by reducing the albedo to less than 1%. So they may save on CO₂ emissions but they come with their own drawbacks, particularly if you live near them. And if they are added to roofs of buildings in cities and urban areas, they will substantially warm those areas.

Net effect on global warming: small increase in local temperatures.

iv) Heat production

There is one UHI effect that does significantly affect temperatures though: waste heat. This is where human energy use ends up as waste heat that heats the local environment around where the energy is being used. As I showed first in Post 14 and later in Post 29, this direct anthropogenic surface heating (DASH) can warm suburbs, cities and even whole countries by up to 1°C. But in fact even that warming is small compared to large cities like London. 

In 2013 the total energy use in Greater London from all sources was estimated at over 150,000 GWh. That is equivalent to an average power consumption of over 15 GW throughout the year. As the area of Greater London is about 1569 km², this amounts to a constant power density of 9.6 W/m². In Post 14 I explained how increasing the 161 W/m² of solar radiation absorbed by the Earth's surface by 2.25 W/m² would be sufficient to increase the mean surface temperature by 1°C. But I also explained that any other source of heat that was absorbed or produced at the surface would have the same effect. So 2.25 W/m² of waste heat generated at the surface would also lead to 1°C of warming.

In London the waste heat will amount to 9.6 W/m², more or less the same as the total power usage. This is because, according to the second law of thermodynamics, all energy is destined to end up as heat or entropy eventually. So waste heat is probably responsible for over 4°C of warming in London - not a great shock to people who live there. That is the urban heat island effect (UHI).

Of course not everyone sees it this way. In climate science this warming is dismissed as trivial because it only amounts to 0.028 W/m² of power use when averaged across the entire surface of the Earth, and so it only raises global mean temperatures by about 0.01°C. While this is technically correct, it neglects the uneven distribution of both these heat sources and the weather stations that determine the global temperature. Most weather stations are on land, almost 90% are in the Northern Hemisphere, and most of these are in the USA, Europe and China. So a high proportion are going to be distorted by the UHI effect from waste heat. That is what makes it important.

Net effect on global warming: large increase in large cities and much of Europe and the USA.

Summary

What I have shown here is that most types of urban heat island (UHI) have little or no effect on global warming with one exception: waste heat. This can add several degrees to the local temperatures.

However, even this is not the full story because the existence UHIs of themselves is not the only issue. Just because a small area of the Earth's surface retains or produces more heat than another does not mean that overall temperatures will rise and add to global warming. It is the change in heat retention and emission over time that is important, not the magnitude or difference from the rest of the environment. A UHI has no impact on global warming if its energy usage is not changing over time. Unfortunately in most cases the energy usage has changed, and by a large amount.

In the next six posts I will highlight six extreme examples of UHIs in the Southern Hemisphere. These are all examples of UHIs in large cities where the UHI temperature has increased much faster than that seen in the country or region as a whole, probably due to significant growth in the size, population and energy use in those cities.

98. What happened to Louisiana temperatures in 1957?

Fig. 98.1: Global average land temperatures since 1850 according to Berkeley Earth.

In my previous post looking at the temperature trend for Louisiana (Post 97) I showed that the mean temperature in the region had declined by almost 0.2°C in the last century or so. This is in sharp contrast to the claim from most climate scientists that average temperatures have increased by almost 1.2°C in that time, and that this increase is even greater on land. In fact Berkeley Earth claims the increase in land temperatures since 1850 to be in excess of 2°C (see Fig. 98.1 above). But while analysing the Louisiana data one feature stood out that makes me query both the results of my last post and the analysis processes of Berkeley Earth (BE). 

In 1957 the temperature appears to drop suddenly and permanently by about 0.615°C (see black arrow on Fig. 98.2 below). What makes this feature significant is that similar temperature falls at identical times can be seen in the most of the individual temperature records for Louisiana. But they can also be seen in the temperature trends of neighbouring states like Texas. 

So is this temperature drop due to a sudden and large, natural change in the local climate? Or is it due to a change in the data measurement and analysis? If it is the latter then it needs to be corrected for and that will change drastically the true temperature trend. If it is the former then it raises serious questions about how the climate changes over time. In this post I will look at this feature in more detail and try to answer those questions.

 

Fig. 98.2: The mean temperature change for Louisiana relative to the 1951-1980 monthly averages. The best fit (white line) is applied to the monthly mean data from 1911 to 2010 and has a negative gradient of -0.38 ± 0.15 °C per century. The arrow and red line indicate the position and size of the data discontinuity.

The data in Fig. 98.2 above is the part of the same data that was presented previously in Fig. 97.1 of Post 97. In this case I am concentrating only on data after 1910 which, as I pointed out in Post 97, is the most reliable as it all results from an averaging of over forty distinct temperature records (see Fig. 97.2). The white line in Fig. 98.2 is the best fit to the data from 1911 to 2010 and has a strong negative gradient of -0.38°C per century. This is somewhat more negative than the trend in Fig. 97.1 because the fitting range is different. This shows how the value of the best fit gradient can be strongly influenced by the data range, particularly when the data exhibits large fluctuations.

The point of interest in the data above is in 1957 (as indicated by the large black arrow) where the mean temperature appears to drop suddenly and permanently by about 0.615°C. This can be seen clearly in the yellow line which is the 5-year moving average of the monthly anomaly data. It is also illustrated by the red line which is effectively two separate lines: the average temperature for 1921-1960 and the average for 1961-1990. In both cases the discontinuity is clear. The magnitude of the vertical discontinuity can be estimated from the discontinuity in the red line and is 0.615°C. 

Fig. 98.3: The mean temperature change for Louisiana after breakpoint adjustment. The best fit is applied to the monthly mean data from 1911 to 2010 and has a positive gradient of +0.54 ± 0.15 °C per century.

The next step is to remove the discontinuity by shifting upwards all the data after the start of 1958 in Fig. 98.2 by the size of the discontinuity, 0.615°C. The result is shown in Fig. 98.3 above. Two things are striking about the result. First, the gradient of the best fit is now strongly positive (+0.54°C per century) suggesting that the climate is warming. And secondly, the data just looks better with a more consistent trend. Of course just because data looks nicer does not prove that it is more reliable or more accurate.

 

Fig. 98.4: The total contribution of Berkeley Earth (BE) adjustments to the Louisiana temperature data. The orange curve shows the contribution just from breakpoint adjustments. The blue curve represents the total BE adjustments including those from homogenization. The linear best fit (red line) to the total BE adjustments for the period 1911-2010 has a positive gradient of +0.731 ± 0.004 °C per century.

The process I have employed here is virtually identical in concept to the breakpoint adjustments used by Berkeley Earth (BE). The main difference is that I have only applied one adjustment to the final mean temperature data whereas Berkeley Earth apply multiple adjustments of differing magnitudes and times to almost every station dataset. The sum total of those BE adjustments for the Louisiana data is shown in Fig. 98.4 above and the result is a huge warming trend of +0.73°C per century. This is warming that is added to the original data as I showed in Post 97. Yet the 0.6°C discontinuity in the middle of 1957 still remains in the adjusted BE data even after their adjustments have been made as the arrow in Fig. 98.5 below indicates. So the BE adjustments have not corrected the most glaring issue with the original data, which does rather raise a lot of questions regarding the accuracy and validity of the BE adjustments that are made.

Fig. 98.5: Temperature trends for Louisiana based on Berkeley Earth adjusted data from the 90 longest station data records. The best fit linear trend line (in red) is for the period 1911-2010 and has a gradient of +0.37 ± 0.05°C/century.

This is not the first time I have encountered these sudden jumps in temperature data. A similar upward jump in temperature of over 1°C can be seen in the temperature trend for Europe in 1988 (see Fig. 44.1 in Post 44). So what is the cause? At the moment I can only think of two explanations: a natural phenomenon that suddenly changes the local climate, or a sudden change in measurement equipment or methodology that is applied across all stations in a region simultaneously. But so far I can find no evidence for either. Of course the natural phenomenon may not have occurred in 1957 or at any other recent time before that. The complex dynamics of the Earth's climate could mean we are seeing the ripples now of forcing events many centuries ago. In Post 9 and Post 17 I have investigated chaotic effects in the temperature record and found evidence of fractal behaviour that can persist for centuries.

Fig. 98.6: The mean temperature change for Texas relative to the 1961-1990 monthly averages. The best fit (white line) is applied to the monthly mean data from 1911 to 2010 and has a negative gradient of -0.15 ± 0.15 °C per century. The arrow and red line indicate the position and size of the data discontinuity.

What is clear is that this temperature discontinuity is not restricted to Louisiana. The same data anomaly can be seen in the temperature trend for Texas that I analysed in Post 52. This is shown in Fig. 98.6 above with the breakpoint adjusted temperatures shown in Fig. 98.7 below.

 

 Fig. 98.7: The mean temperature change for Texas after breakpoint adjustment. The best fit is applied to the monthly mean data from 1911 to 2010 and has a positive gradient of +0.56 ± 0.15 °C per century.

After the breakpoint adjustment the temperature trend for Texas is now positive and virtually identical to that of Louisiana in Fig. 98.3. There also appears to be a strong correlation between the 5-year moving average (yellow curves) of each. This suggests that the region could have warmed by about 0.5°C over the last one hundred years. However, as I pointed out in Post 52, direct anthropogenic surface heating (DASH) or waste heat equating to about 0.7 W/m² is probably currently warming Texas by up to 0.3 °C compared to 1850. That only leaves about 0.2°C for carbon dioxide induced climate change. This in line with the temperature rise I estimated in Post 87 and a long way short of the 2°C claimed by Berkeley Earth and others. So even with this adjustment there is little evidence to support severe carbon dioxide induced climate change in Louisiana or Texas.

50. Poland - temperature trends WARMING 0.9°C

There are over 100 temperature records for Poland. The longest is the Warsaw record (Berkeley Earth ID: 157587) which dates back to 1779 (see Fig. 50.1 below) and exhibits a strong warming trend of 0.71 °C per century. However, this warming trend is not continuous but has considerable variability, with temperatures in the 1930s being comparable to those of today.

 

Fig. 50.1: The temperature trend for Warsaw since 1779. The best fit is applied to the interval 1811-2010 and has a positive gradient of +0.71 ± 0.08 °C per century. The monthly temperature changes are defined relative to the 1951-1980 monthly averages. 

 

Of the 100 or more stations in Poland (for a full list see here), 60 have over 480 months of data (these are medium stations) and five have over 1200 months of data (long stations). In fact over 40 of the medium station have over 720 months (or 60 years) of data which is fairly unusual. This is because there was a significant and abrupt increase in the number of weather station records in Poland in 1951. Similar investments in new stations are seen in many other countries as well in the latter part of the 20th century, but these tend to occur around 1960 or 1970-1973.

The locations of these long and medium stations are shown below in Fig. 50.2. The map indicates that the stations are fairly evenly distributed across Poland which means that a simple average of the anomalies from all these stations should approximate very well to the temperature trend for the country as a whole.

Fig. 50.2: The locations of long stations (large squares) and medium stations (small diamonds) in Poland. Those stations with a high warming trend are marked in red. 

 

In order to determine the mean temperature change for Poland, I first calculated the temperature anomalies for each temperature record relative to its monthly means (MRTs) for the period 1951-1980. These anomalies were then averaged to produce the trend shown in Fig. 50.3 below.

The 1951-1980 interval was chosen because it allowed the maximum number of stations to be included in the mean (see Fig. 50.4 below) while also avoiding the sudden jump in temperatures seen around 1988 in many European temperature records (see Post 44 and Post 49) that could destabilize the MRTs. For a moredetailed description of how the monthly reference temperatures (MRTs) are calculated and why, please refer to Post 47.

 

Fig. 50.3: The temperature trend for Poland since 1779. The best fit is applied to the interval 1811-2010 and has a positive gradient of +0.45 ± 0.08 °C per century. The monthly temperature changes are defined relative to the 1951-1980 monthly averages. 

While the trend in Fig. 50.3 above is the result of averaging over 60 separate records, no more than 58 are included in any single monthly average, and before 1950 this is typically less than ten (see Fig. 50.4 below). Overall, the temperature trend exhibits a significant warming of about 0.9 °C since 1800, but this is much less than that seen in the trend for Warsaw as shown in Fig. 50.1 above. The difference is almost certainly due to anthropogenic effects such as the urban heat island (UHI) effect or waste heat emissions from human and industrial activity. Overall such direct anthropogenic surface heating (DASH) would be expected to increase the temperature of the whole of Poland by about 0.2 °C.

The other detail that is noticeable about the data in Fig. 50.3 is that the temperatures in the 1930s were similar to those of today. This is despite temperatures appearing to have jumped suddenly by about 0.84 °C in 1988. A similar and larger jump of 0.97 °C was seen in the temperature data across Germany at the same time (see Post 49).

Fig. 50.4: The number of station records included each month in the mean temperature trend for Poland when the MRT interval is 1951-1980.

What is clear is that the warming seen in Poland, while significant, is much less than that expected based on IPCC and Berkeley Earth reports. These have suggested that the warming is over 1.5 °C and fairly monotonic. In reality there is a large amount of what looks like natural variation in the data that persists even for very long time-averaged data such as the 5-year moving average.

Fig. 50.5: Temperature trend in the Poland since 1779 derived by aggregating and averaging the Berkeley Earth adjusted data for all long and medium stations. The best fit linear trend line (in red) is for the period 1801-1980 and has a gradient of +0.32 ± 0.03 °C/century.

For comparison, the temperature trend that results from averaging the temperature data after it has been adjusted by Berkeley Earth is shown in Fig. 50.5 above. This trend shows a modest warming of 0.32 °C per century before 1980, or about 0.6 °C in total, followed by a major temperature increase of over 1 °C after 1980. This trend is also virtually identical to the one published by Berkeley Earth (see here) as shown in Fig. 50.6 below.

Fig. 50.6: The temperature trend for Poland since 1750 according to Berkeley Earth.

If we look at the difference between the mean trend in Fig. 50.3 (based on the original true data) and the trend in Fig. 50.5 that is the result of using the Berkeley Earth adjusted data we see that the adjustments made by Berkeley Earth are again not neutral. In fact the Berkeley Earth adjustments add nearly 0.6 °C of warming since 1840 (see Fig. 50.7 below).

Fig. 50.7: The contribution of Berkeley Earth (BE) adjustments to the anomaly data in Fig. 50.5 after smoothing with a 12-month moving average. The blue curve represents the total BE adjustments including those from homogenization. The linear best fit (red line) to these adjustments for the period 1841-2010 has a gradient of +0.335 ± 0.007 °C per century. The orange curve shows the contribution from breakpoint adjustments.

Conclusions

It is clear from the results shown here that temperatures in Poland have increased over the last 250 years, but by how much and for what reason remains unclear. There has certainly not been the catastrophic warming due to carbon dioxide emissions (i.e. more than 1.5 °C) that has been claimed by climate scientists, although there might have been some warming from this source. However, such warming cannot realistically be greater than 0.7 °C (i.e. the 0.9 °C seen in Fig. 50.3 minus the 0.2 °C we would expect from DASH or UHI effects). The problem is that any remaining warming that may be due to CO₂ emissions does not correlate well with CO₂ levels in the atmosphere over time. And then there is the uncertainty over the amount that natural variation in the temperature record may be contributing to the relatively short-term trends (less than 250 years) that we are observing.

We can probably claim with a fair degree of confidence that the data after 1950 in Fig. 50.3 is likely to be highly reliable as it is based on over 50 station records that are evenly spaced geographically (see Fig. 50.2). But this raises the question of what is causing the sudden jump in temperatures seen in 1988 which is also seen in other countries such as Germany (see Post 49).

For data before 1950, this is based on between about four and ten station records, at least back to 1830. The overall trend for 1831-1980 suggests a total temperature rise of only about 0.35 ± 0.15 °C, which is less than the standard deviation of the temperature fluctuations in the 5-year moving average for that period. This suggests that these temperature changes could be explained by natural variability.

Finally, it is apparent that once again there is a large discrepancy (0.6 °C) between any temperature rises seen in the raw data (see Fig. 50.3) and the rises claimed by climate scientists (see Fig. 50.5). This difference is largely due to adjustments made to the raw data by climate scientists (see Fig. 50.7).

45. Review of the year 2020

I started this blog in May, in part to occupy my time during the Covid-19 lockdown. But I was also motivated by a growing dissatisfaction with the quality of data analysis I was witnessing in climate science, and in particular the lack of any objectivity in the way much of the data was being presented and reported. My concerns were twofold. 

The first was the drip-drip of selective alarmism with an overt confirmation bias that kept appearing in the media with no comparable reporting of events that contradicted that narrative. The worry here is that extreme events that are just part of the natural variation of the climate were being portrayed as the new normal, while events of the opposite extreme were being ignored. It appeared that balance was being sacrificed for publicity.

The second was the over-reliance of much of the climate analysis on complex statistical analysis techniques of doubtful accuracy or veracity. To paraphrase Lord Rutherford: if you need to use complex statistics to see any trends in your data, then you would be better off using better data. Or to put it more simply, if you can't see a trend with simple regression analysis, then the odds are there is no trend to see.

The purpose of this blog has not been to repeat the methods of climate scientists, nor to improve on them. It has merely been to set a benchmark against which their claims can be measured and tested.

My first aim has been to go back to basics, to examine the original temperature data, look for trends in that data, and to apply some basic error analysis to determine how significant those trends really are. Then I have sought to compare what I see in the original data with what climate scientists claim is happening. In most cases I have found that the temperature trends in the real data are significantly less than those reported by climate scientists. In other words, much of the reported temperature rises, particularly in Southern Hemisphere data, result from the data manipulations performed by the climate scientists on the data. This implies that many of the reported temperature rises are an exaggeration.

In addition, I have tried to look at the physics and mathematics underpinning the data in order to test other possible hypotheses that could explain the observed temperature trends that I could detect. Below I have set out a summary of my conclusions so far.

1) The physics and mathematics

There are two alternative theories that I have considered as explanations of the temperature changes. The first is natural variation. The problem here is that in order to conclusively prove this to be the case you need temperature data that extends back in time for dozens of centuries, and we simply do not have that data. Climate scientists have tried to solve this by using proxy data from tree rings and sediments and other biological or geological sources, but in my opinion these are wholly inadequate as they are badly calibrated. The idea that you can measure the average annual temperature of an entire region to an accuracy of better than 0.1 °C simply by measuring the width of a few tree rings, when you have no idea of the degree of linearity of your proxy, or the influence of numerous external variables (e.g. rainfall, soil quality, disease, access to sunlight), is preposterous. But there is another way.

i) Fractals and self-similarity

If you can show that the fluctuations in temperature over different timescales follow a clear pattern, then you can extrapolate back in time. One such pattern is that resulting from fractal behaviour and self-similarity in the temperature record. By self-similarity I mean that every time you average the data you end up with a pattern of fluctuations that looks similar to the one you started with, but with amplitudes and periods that change according to a precise mathematical scaling function.

In Post 9 I applied this analysis to various sets of temperature data from New Zealand. I then repeated it for data from Australia and then again in Post 42 for data from De Bilt in the Netherlands. In virtually all these cases I found a consistent power law for the scaling parameter indicative of a fractal dimension of between 0.20 and 0.30, with most values clustered close to 0.25. The low magnitude of this scaling term suggests that the fluctuations in long term temperatures are much greater in amplitude than conventional statistical analysis would predict. 

For example, in the case of De Bilt it suggests that the standard deviation in the average 100-year temperature is more than 0.2 °C. This means that there is a 16% probability of the mean temperature for any century being more than 0.3°C more (or less) than the mean temperature for the previous century, and therefore a one in six possibility of a 0.6 °C temperature rise in any given century. So a 0.6 °C temperature rise over a century could occur once every 600 years purely because of natural variations in temperature. It also suggests that similar temperature variations that we have seen in temperature data in the last 50 or 100 years might have been repeated frequently in the not so distant past.

ii) Direct anthropogenic surface heating (DASH) and the urban heat island (UHI)

Another possible explanation for any observed rise in temperature is the heating of the environment that occurs due to human industrial activity. All energy use produces waste heat. Not only that, but all energy must end up as heat and entropy in the end. The Second Law of Thermodynamics tells us that. It is therefore inevitable that human activity must heat the local environment. The only question is by how much.

Most discussions in this area focus on what is known as the urban heat island (UHI). This is a phenomenon whereby urban areas either absorb extra solar radiation because of changes made to the surface albedo by urban development (e.g. concrete, tarmac, etc), or tall buildings trap the absorbed heat and reduce the circulation of warm air, thereby concentrating the heat. But there is another contribution that continually gets overlooked - direct anthropogenic surface heating (DASH). 

When humans generate and consume energy they liberate heat or thermal energy. This energy heats up the ground, and the air just above it, in much the same way that radiation from the Sun does. In so doing DASH adds to the heat that is re-emitted from the Earth's surface, and therefore increases the Earth's surface temperature at that location.

In Post 14 I showed that this heating can be significant - up to 1 °C in countries such as Belgium and the Netherlands with high levels of economic output and high population densities. In Post 29 I extended this idea to look at suburban energy usage and found a similar result. 

What this shows is that you don't need to invoke the Greenhouse Effect to find a plausible mechanism via which humans are heating the planet. Simple thermodynamics will suffice. Of course climate scientists dismiss this because they assume that this heat is dissipated uniformly across the Earth's surface - but it isn't. And just as significant is the fact that the majority of weather stations are in places where most people live, and therefore they also tend to be in regions where the direct anthropogenic surface heating (DASH) is most pronounced. So this direct heating effect is magnified in the temperature data.

iii) The data reliability

It is taken as read that the temperature data used to determine the magnitude of the observed global warming is accurate. But is it? Every measurement has an error. In the case of temperature data it appears that these errors are comparable in magnitude to many of the effects climate scientists are trying to measure.

In Post 43 I looked at pairs of stations in the Netherlands that were less than 1.6 km apart. One might expect that most such pairs would exhibit identical datasets for the two stations in the pair, but they don't. In virtually every case the fluctuations in the difference in their monthly average temperatures was about 0.2 °C. While this was consistent with the values one would expect based on error analysis, it does highlight the limits to the accuracy of this data. It also raises questions about how valid techniques such as breakpoint adjustment are, given that these techniques depend on detecting relatively small differences in temperature for data from neighbouring stations.

iv) Temperature correlations between stations

In Post 11 I looked at the product moment correlation coefficients (PMCC) between temperature data from different stations, and compared the correlation coefficients with the station separation. What became apparent was evidence for a strong negative linear relationship between the maximum correlation coefficient for temperature anomalies between pairs of station and their separation. For station separations of less than 500 km positive correlations of better than 0.9 were possible, but this dropped to a maximum correlation of about 0.7 for separations of 1000 km and 0.3 at 2000 km.

There were also clear differences between the behaviour of the raw anomaly data and the Berkeley Earth adjusted data. The Berkeley Earth adjustments appear to reduce the scatter in the correlations for the 12-month averaged data, but do so at the expense of the quality of the monthly data. This suggests that these adjustments may be making the data less reliable not more so. The improvement in the scatter of the Berkeley Earth 12-month averaged data is also curious. Is it because it is this data that is used to determine the adjustments and not the monthly data, or is this not the case and instead there is some other reason? And what of the scatter in the data? Can we use this to measure the quality and reliability of the original data? This clearly warrants further study.

Fig. 45.1: Correlations (PMCC) for the period 1971-2010 between temperature anomalies for all stations in New Zealand with a minimum overlap of 200 months. Three datasets were studied: a) the monthly anomalies; b) the 12-month average of the monthly anomalies; c) the 5-year average of the monthly anomalies. Also studied were the equivalent for the Berkeley Earth adjusted data.

2) The data

Over the last eight months I have analysed most of the temperature data in the Southern Hemisphere as well as all the data in Europe that predates 1850. The results are summarized below.

i) Antarctica

In Post 4 I showed that the temperature at the South Pole has been stable since the 1950s. There is no instrumental temperature data before 1956 and there are only two stations of note near the South Pole (Amundsen-Scott and Vostok). Both show stable or negative trends.

Then in Post 30 I looked at the temperature data from the periphery of the continent. This I divided into three geographical regions: the Atlantic coast, the Pacific coast and the Peninsula. The first two only have data from about 1950 onwards. In both cases the temperature data is also stable with no statistically significant trend either upwards or downwards. Only the Peninsula exhibited a strong and statistically significant upward trend of about 2 °C since 1945.

ii) New Zealand

Fig. 45.2: Average warming trend of for long and medium stations in New Zealand. The best fit to the data has a gradient of +0.27 ± 0.04 °C per century.

In Posts 6-9 I looked at the temperature data from New Zealand. Although the country only has about 27 long or medium length temperature records, with only ten having data before 1880, there is sufficient data before 1930 to suggest temperatures in this period were almost comparable to those of today. The difference is less than 0.3 °C.

iii) Australia

Fig. 45.3: The temperature trend for Australia since 1853. The best fit is applied to the interval 1871-2010 and has a gradient of 0.24 ± 0.04 °C per century.

The temperature trend for Australia (see Post 26) is very similar to that of New Zealand. Most states and territories exhibited high temperatures in the latter part of the 19th century that then declined before increasing in the latter quarter of the 20th century. The exceptions were Queensland (see Post 24) and Western Australia (see Post 22), but this was largely due to an absence of data before 1900. While there is much less temperature data for Australia before 1900 compared to the latter part of the 20th century, there is sufficient to indicate that, as in New Zealand, temperatures in the late 19th century were similar to those of the present day.

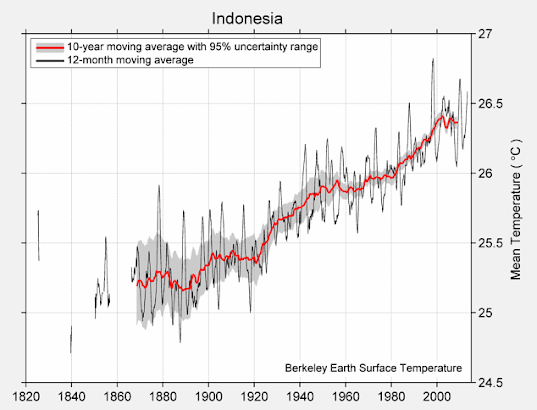
iv) Indonesia

Fig. 45.4: The temperature trend for Indonesia since 1840. The best fit is applied to the interval 1908-2002 and has a negative gradient of -0.03 ± 0.04 °C per century.

The temperature data for Indonesia is complicated by the lack of quality data before 1960 (see Post 31). The temperature trend after 1960 is the average of between 33 and 53 different datasets, but between 1910 and 1960 it generally comprises less than ten. Nevertheless, this is sufficient data to suggest that temperatures in the first half of the 20th century were greater than those in the latter half. This is despite the data from Jakarta Observatorium which exhibits an overall warming trend of nearly 3 °C from 1870 to 2010 (see Fig. 31.1 in Post 31).

It is also worth noting that the temperature data from Papua New Guinea (see Post 32) is similar to that for Indonesia for the period from 1940 onwards. Unfortunately Papua New Guinea only has one significant dataset that predates 1940, so conclusions regarding the temperature trend in this earlier time period are difficult to ascertain.

v) South Pacific

Most of the temperature data from the South Pacific comes from the various islands in the western half of the ocean. This data exhibits little if any warming, but does exhibit large fluctuations in temperature over the course of the 20th century (see Post 33). The eastern half of the South Pacific, on the other hand, exhibits a small but discernible negative temperature trend of between -0.1 and -0.2 °C per century (see Post 34).

vi) South America

Fig. 45.5: The temperature trend for South America since 1832. The best fit is applied to the interval 1900-1999 and has a gradient of +0.54 ± 0.05 °C per century.

In Post 35 I analysed over 300 of the longest temperature records from South America, including over 20 with more than 100 years of data. The overall trend suggests that temperatures fluctuated significantly before 1900 and have risen by about 0.5 °C since. The high temperatures seen before 1850 are exclusively due to the data from Rio de Janeiro and so may not be representative of the region as a whole.

vii) Southern Africa

Fig. 45.6: The temperature trend for South Africa since 1840. The best fit is applied to the interval 1857-1976 and has a gradient of +0.017 ± 0.056 °C per century.

In Posts 37-39 I looked at the temperature trends for South Africa, Botswana and Namibia. Botswana and Namibia were both found to have less than four usable sets of station data before 1960 and only about 10-12 afterwards. South Africa had much more data, but the general trends were the same. Before 1980 the temperature trends were stable or perhaps slightly negative, but after 1980 there was a sudden rise of between 0.5 °C and 2 °C in all three trends, with the largest being found in Botswana. This does not correlate with accepted theories on global warming (the rises in temperature are too large and too sudden, and do not correlate with rises in atmospheric carbon dioxide), and so the exact origin of these rises appears to be unexplained.

 

viii) Europe

Fig. 45.7: The temperature trend for Europe since 1700. The best fit is applied to the interval 1731-1980 and has a positive gradient of +0.10 ± 0.04 °C per century.

In Post 44 I used the 109 longest temperature records to determine the temperature trend in Europe since 1700. The resulting data suggests that temperatures were stable from 1700 to 1980 (they rose by less than 0.25 °C), and then rose suddenly by about 0.8 °C after 1986. The reason for this change is unclear, but one possibility is that it has occurred due to a significant improvement in air quality that reduced the amount of particulates in the atmosphere. These particulates, that may have been present in earlier years, could have induced a cooling that compensated for the underlying warming trend. Once removed, the temperature then rebounded. Even if this is true, it suggests a maximum warming of about 1 °C since 1700, much of which could be the result of direct anthropogenic surface heating (DASH) as discussed in Post 14. In countries such as Belgium and the Netherlands the temperature rise is even less than that expected from such surface heating. It is also much less than that expected from an enhanced Greenhouse Effect due to increasing carbon dioxide levels in the atmosphere (i.e. about 1.5 °C in the Northern Hemisphere since 1910). In fact the total temperature rise should exceed 2.5 °C. So here is the BIG question? Where has all that missing temperature rise gone?

31. Indonesia - temperature trends STABLE

Indonesia is one of the largest countries in the world and has one of the largest populations at over 267 million. Its archipelago of islands straddles the equator and stretches from a longitude of 95°E to 141°E, a distance of over 5000 km. The country has 53 medium length temperature records with between 480 and 1200 months of data, but only one long station record with more than 1200 months of data (see here). That station is Jakarta Observatorium (Berkeley Earth ID: 155660). It is also the station with the most pronounced warming trend (see Fig. 31.1 below).

Fig. 31.1: The temperature trend for Jakarta Obervatorium since 1866. The best fit is applied to the interval 1866-2013 and has a gradient of 1.82 ± 0.08 °C per century. The temperature changes are relative to the 1961-1990 average.

Overall the temperature rise for Jakarta Obseratorium is nearly 2.7 °C from 1866 to 2013, yet this is not representative of the country as a whole. The medium stations in Indonesia exhibit both warming and stable trends as shown in Fig. 31.2 below. In this case stable trends are defined to be those with a warming that is less than twice the uncertainty. The stations are also fairly evenly dispersed, but are mainly coastal.

Fig. 31.2: The locations of long stations (large squares) and medium stations (small diamonds) in Indonesia. Those stations with a high warming trend are marked in red.

If we average all the records from the long and medium stations we get the overall trend shown in Fig. 31.3 below. Instantly we see a problem. While the overall trend since 1908 appears to be negative (-0.03 ± 0.04 °C per century in fact), there are large discontinuities around 1860, 1902 and 1941.

Fig. 31.3: The temperature trend for Indonesia since 1840. The best fit is applied to the interval 1908-2002 and has a negative gradient of -0.03 ± 0.04 °C per century. The temperature changes are relative to the 1961-1990 average.

 

The reason for this is the low number of station records before 1950, as illustrated in Fig. 31.4 below. For example, between 1866 and 1903 there is only one temperature record available, that of Jakarta Observatorium illustrated in Fig. 31.1 above.

Fig. 31.4: Number of stations per month included in the regional average for the Indonesia temperature anomaly. Only stations with more than 240 months of data in total and sufficient data in the period 1961-1990 are counted.

 

That is not the only problem, though. Low station numbers means that the average can be heavily distorted by one or two rogue datasets, and in this case there are at least three potential candidates in addition to Jakarta Obseratorium in Fig. 31.1. They are shown in the three figures below.

Fig. 31.5: The temperature trend for Christmas Island (Berkeley Earth ID: 154345) since 1900.

Fig. 31.6: The temperature trend for Padang (Berkeley Earth ID: 155706) since 1850.

Fig. 31.7: The temperature trend for Jakarta (Berkeley Earth ID: 15412) since 1866.

The last of these (Fig. 31.7) is another temperature record from Jakarta. Although this has none of the large temperature offsets seen in Fig. 31.5 and Fig. 31.6, it does appear to be as anomalous as the Jakarta Observatorium data in that it is inconsistent with the rest of the data for the country. It is also in close proximity to an existing station (Jakarta Observatorium). So, on the one hand it can corroborate the trend from Jakarta Observatorium, but on the other hand the weightings of both in the overall average trend should be halved.

The remaining question is whether the large temperature falls seen after 1950 in Fig. 31.5 and Fig. 31.6 are real. The suspicion (and it is just a suspicion) is that they are real because similar falls occur in too many other records. For example, they can also be seen in records from Dilli, Bandung and Pontianak. 

 

Fig. 31.8: The temperature trend for Indonesia since 1900 excluding the temperature records from Jakarta. The best fit is applied to the interval 1913-2012 and has a negative gradient of -0.08 ± 0.04 °C per century. The temperature changes are relative to the 1961-1990 average.

So, rather than discarding the data from Christmas Island (Fig. 31.5) and Padang (Fig. 31.6), what happens if we discard both the datasets from Jakarta (Fig. 31.1 and Fig. 31.7) instead? The result is the trend shown in Fig. 31.8 above. This has a negative trend of -0.08 ± 0.04 °C per century, a trend which is also consistent with the data around 1850. The only anomaly is the data from 1903-1913 that is solely from Christmas Island. 

The conclusion from this is that the only part of Indonesia that has exhibited any significant warming since 1850 is the capital and largest city, Jakarta. The rest of the country has seen no temperature rise at all.

Fig. 31.9: Temperature trend for all long and medium stations in Indonesiasince 1850 derived using the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1871-2010 and has a gradient of +0.94 ± 0.03 °C/century.

What we need to do next is compare the results illustrated above, derived using the anomalies from the raw temperature data, with the equivalent results from Berkeley Earth. Summing and averaging the adjusted anomalies from Berkeley Earth yields the graph in Fig. 31.9 above. These are very similar to the published curves from Berkeley Earth shown in Fig. 31.10 below. Most of the differences are likely due to the inclusion of additional of smaller datasets in the Berkeley Earth plots.

The gradient of the best fit in Fig. 31.9 is +0.94 ± 0.03 °C per century. This is about half that seen in the data for Jakarta Observatorium shown in Fig. 31.1 above, but completely at odds with the data for the rest of the country shown in Fig. 31.8. It suggests that the temperature data from Jakarta has been assigned a greater level of significance (or weighting) and confidence than data from elsewhere in Indonesia. This is perhaps not surprising. The two records from Jakarta are two of the longest and most complete. They also exhibit trends that are both smooth and monotonic. But that does not mean their greater weighting is justified.

Fig. 31.10: Temperature trend for Indonesia since 1840 according to Berkeley Earth.

If we compare the Berkeley Earth adjusted data shown in Fig. 31.9 with the original raw unadjusted anomalies shown in Fig. 31.3, the difference is significant. This difference is shown in Fig. 31.11 below.

Fig. 31.11: The contribution of Berkeley Earth (BE) adjustments to the anomaly data after smoothing with a 12-month moving average. The linear best fit to the data is for the period 1904-2012 (red line) and the gradient is +0.96 ± 0.03 °C per century. The orange curve represents the contribution made to the BE adjustment curve by breakpoint adjustments only.

The data in Fig. 31.11 is shocking. If my analysis is correct, then it suggests that the adjustments made to the data by Berkeley Earth could have added about 0.95 °C to the warming trend since 1904. In other words, virtually all the warming claimed by Berkeley Earth to have occurred in Indonesia since 1904, and depicted in Fig. 31.10, may be the result of their own data adjustments, and not the original data. Moreover, most of this added warming appears to come from breakpoint adjustments.

Conclusions

1) The only warming seen in Indonesia appears to have occurred in Jakarta (see Fig. 31.1). 

2) This warming has been large (about 2.7 °C) and continuous since 1866, which is consistent with its source being population growth linked to increased energy consumption and direct anthropogenic surface heating (DASH), as discussed in Post 14 and Post 29. It may also be a consequence of the urban heat island (UHI) effect.

3) There has been no warming of the overall climate in Indonesia since 1900 (see Fig. 31.8 below).