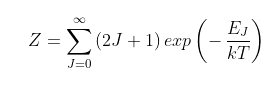127: The urban heat island (UHI) effect - an explainer

 

The urban heat island (UHI) effect.

 

The conventional wisdom is that climate change is driven by rising carbon dioxide (CO₂) levels in the atmosphere, and only by CO₂; so the greater the (CO₂) levels the greater the temperature increase (see Fig. 87.3 in Post 87). You may have noticed one direct consequence of this orthodoxy in the way the media these days reports on environmental disasters or extreme weather (floods, droughts, storms, hurricanes, heatwaves, forest fires etc.): they always refer to climate change.

Implicit to this climate change reference is the assumption that all climate change is due to CO₂ even though CO₂ is rarely explicitly mentioned and the causation is rarely demonstrated. Consequently, the solution to all extreme weather events appears to be simple and obvious: cut CO₂ levels in the atmosphere (i.e. Net Zero) and everything will be fine. Except it won't. This is because much of what is happening to local climates has little or nothing to do with CO₂, but it does have a lot to do with other human activities, not least urbanization and industrialization. Central to both of these is the urban heat island (UHI) effect.

The problem when discussing the impact of the UHI effect on climate, and in particular the temperature record, is that it is controversial. This is partly because much of climate science appears to be driven by an anti-fossil fuel dogma that therefore sees any talk of UHIs as at best a distraction from the supposed only true problem, CO₂, and at worst a campaign of disinformation designed to undermine all of climate science and its campaign against CO₂. But it is also partly because UHIs come in many flavours. 

There are those UHIs that just trap more heat by reducing airflows and those that store more solar heat than rural areas by virtue of increased heat capacities. Both of these do not add to the total amount of energy absorbed at the Earth's surface though, so there is no net global temperature increase associated with them. But then there are those UHI processes that do absorb extra heat, either via changes to the albedo of the Earth's surface, or by the emission of large amounts of additional heat through anthropogenic energy use and generation. Both of these certainly do add to global warming but are still largely ignored by climate science. In the following sections I will discuss the relative impact of each of these four types of UHI effect in turn and show that one type in particular can be very significant.

i) Heat trapping

The aspect of the UHI effect that is referred to the most is heat trapping. This is where tall buildings in a city reduce the flow of hot air away from the centre causing the city to retain its heat longer. Perhaps the most obvious example of this is Manhattan in New York City with its dense cluster of tall skyscrapers.

The result of this UHI effect is that the local area of the city stays hotter for longer compared to if the buildings were not there. This is because there is less diffusion of heat to outlying areas, so those areas are less likely to be warmed by the city and the city is less likely to be cooled by heat transfer to the rural areas that surround it. 

However, this does not lead to more global warming because while the city will be hotter for longer than otherwise expected, the surrounding area will be cooler for longer as well because less heat from the urban areas reaches the rural areas. The key point here is that no extra heat is created at the surface of the Earth, it is just prevented from diffusing to colder regions. So the net effect on local mean temperatures is zero. As an example consider the Grand Canyon. It will trap heat in the same way that tall buildings do, but does that mean that it is warming faster than the rest of Arizona? No, and nor does it make Arizona as a whole get any warmer.

This is one reason why climate scientists discount the UHI effect, and in this case they are right, provided that the weather stations used to monitor temperature changes are evenly distributed and their temperature readings are not adjusted. Those, unfortunately, are big IFs, because any bias in station numbers between urban and rural regions compared to their relative areas will affect the the relative contribution of each to the mean global temperature, and we do know that station densities are generally higher in urban areas. So potentially there are more warm urban stations contributing to the global average than there should be and fewer cold rural ones. In an ideal world, though, this should not occur, and so neither would any contribution to global temperatures.

Net effect on global warming: zero.

ii) Increased heat capacity

Probably the second most cited variation of the UHI effect is heat retention where cities heat up and store energy from the Sun during the day and then gradually release it overnight. The net effect of this is that the maximum temperature in the city during the day should be less than expected because of the time it takes the buildings to heat up. This is because the Sun is not just heating up the top layer of the Earth's surface, as would be the case in rural areas; it is also having to heat up large concrete structures with much higher heat capacities. The higher the local heat capacity of these structures, the longer it takes to warm them and the slower, and therefore lower, their temperature rise will be. This in turn means that less infra-red radiation is then radiated back into outer space during the day because the region is cooler than it would be without the buildings, and so there is less heating of the lower atmosphere and less downwelling radiation.

At night, however, the heating from the Sun stops. The rural areas cool quickly but the urban areas don't because the urban areas have the much higher heat capacity: there is more heat stored that needs to be lost before a new thermal equilibrium without the Sun can be established. So the buildings are now warmer than their rural surroundings but are slowly cooling, acting like large radiators or storage heaters. This means that the city stays warmer for longer, and temperatures within the city are higher at night than they would otherwise be. 

The net effect of this is that temperatures during the day will be lower, but those at night-time will be higher. Overall, though, the effect on the average temperature will be zero as the two changes in temperature cancel due to the fact that the changes in heat absorption will also cancel.

Net effect on global warming: zero.

iii) Increased heat absorption

One consequence of urban development is that it changes the reflectivity of the Earth's surface for incident visible, ultraviolet and near infra-red radiation. This reflectivity is known as the albedo and it is loosely related to the colour of a surface: darker colours tend to absorb more radiation while lighter ones generally reflect more. If the albedo increases, then more radiation is reflected back into space without heating the planet, so ice and snow help to cool the planet (their albedo is over 80%) while dark soil and oceans tend to warm the planet (see Table 14.1 in Post 14 for a list of typical albedos). It therefore follows that if the colour of a surface changes, then so will its albedo, and this can then change the amount of radiation absorbed at the surface. If this absorbed radiation increases, then the Earth will get warmer and the UHI effect is one way this can happen.

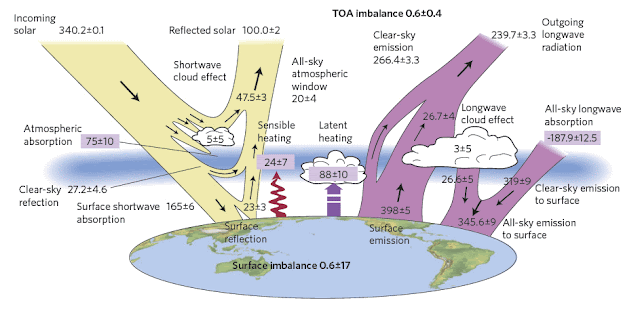
In Post 14 I explained that of the average incoming solar radiation of 341 W/m² that the Earth receives, only 161 W/m² is absorbed at its surface, and that greenhouse gases then amplify this with 333 W/m² of additional downwelling radiation. This total absorbed heat of 494 W/m² then dictates the mean surface temperature via the Stefan-Boltzmann law (see Post 12). It therefore follows that if any change occurs at the Earth's surface that increases the 161 W/m² of absorbed radiation, then this will change the downwelling radiation by the same percentage and therefore change the mean surface temperature as well.

The process of urbanization inevitably involves changing the colour and texture of the Earth's surface. It generally means that areas of vegetation are replaced with tarmac and concrete. Buildings with dark roofs absorb more solar radiation than trees and grassland. However the situation is not straightforward because concrete can be very reflective and arable land tends to be very dark. Overall though, there is generally a small decrease in albedo with urbanization, and therefore a small increase in the amount of solar radiation that is absorbed. This will raise the surface temperature of the Earth slightly as well, but because it is small it is not likely to be significant.

One human innovation that can have a big impact on temperature is solar power. Because solar panels are designed to absorb 99% of solar radiation, they will add additional heating to any area where they are installed by reducing the albedo to less than 1%. So they may save on CO₂ emissions but they come with their own drawbacks, particularly if you live near them. And if they are added to roofs of buildings in cities and urban areas, they will substantially warm those areas.

Net effect on global warming: small increase in local temperatures.

iv) Heat production

There is one UHI effect that does significantly affect temperatures though: waste heat. This is where human energy use ends up as waste heat that heats the local environment around where the energy is being used. As I showed first in Post 14 and later in Post 29, this direct anthropogenic surface heating (DASH) can warm suburbs, cities and even whole countries by up to 1°C. But in fact even that warming is small compared to large cities like London. 

In 2013 the total energy use in Greater London from all sources was estimated at over 150,000 GWh. That is equivalent to an average power consumption of over 15 GW throughout the year. As the area of Greater London is about 1569 km², this amounts to a constant power density of 9.6 W/m². In Post 14 I explained how increasing the 161 W/m² of solar radiation absorbed by the Earth's surface by 2.25 W/m² would be sufficient to increase the mean surface temperature by 1°C. But I also explained that any other source of heat that was absorbed or produced at the surface would have the same effect. So 2.25 W/m² of waste heat generated at the surface would also lead to 1°C of warming.

In London the waste heat will amount to 9.6 W/m², more or less the same as the total power usage. This is because, according to the second law of thermodynamics, all energy is destined to end up as heat or entropy eventually. So waste heat is probably responsible for over 4°C of warming in London - not a great shock to people who live there. That is the urban heat island effect (UHI).

Of course not everyone sees it this way. In climate science this warming is dismissed as trivial because it only amounts to 0.028 W/m² of power use when averaged across the entire surface of the Earth, and so it only raises global mean temperatures by about 0.01°C. While this is technically correct, it neglects the uneven distribution of both these heat sources and the weather stations that determine the global temperature. Most weather stations are on land, almost 90% are in the Northern Hemisphere, and most of these are in the USA, Europe and China. So a high proportion are going to be distorted by the UHI effect from waste heat. That is what makes it important.

Net effect on global warming: large increase in large cities and much of Europe and the USA.

Summary

What I have shown here is that most types of urban heat island (UHI) have little or no effect on global warming with one exception: waste heat. This can add several degrees to the local temperatures.

However, even this is not the full story because the existence UHIs of themselves is not the only issue. Just because a small area of the Earth's surface retains or produces more heat than another does not mean that overall temperatures will rise and add to global warming. It is the change in heat retention and emission over time that is important, not the magnitude or difference from the rest of the environment. A UHI has no impact on global warming if its energy usage is not changing over time. Unfortunately in most cases the energy usage has changed, and by a large amount.

In the next six posts I will highlight six extreme examples of UHIs in the Southern Hemisphere. These are all examples of UHIs in large cities where the UHI temperature has increased much faster than that seen in the country or region as a whole, probably due to significant growth in the size, population and energy use in those cities.

89. The Greenhouse Effect on Mars

In my previous three posts I have explained how the Greenhouse Effect (GHE) works on Earth, and how it is affected by changes to the carbon dioxide (CO₂) concentration in the atmosphere. The problem with studying the GHE on Earth, though, is that its operation is complicated by the presence of large amounts of water vapour in the atmosphere. As water vapour also has a broader absorption band and higher atmospheric concentration than CO₂, this means that changes in the CO₂ concentration are less important than they would be otherwise. If we want to understand and measure the GHE just due to carbon dioxide, then we need an environment with high levels of CO₂ but low levels of other greenhouse gases. In this respect one of the best places to study is Mars. 

The Atmosphere of Mars

The Martian atmosphere has some similarities with Earth but many differences. It contains many of the same gases (nitrogen, oxygen, water vapour, argon, CO₂), but the proportions are vastly different. The atmosphere of Mars is 96% CO₂ with about 2% nitrogen and 2% Argon (although different pages on Wikipedia give slightly different values such as 95% CO₂ and 3% nitrogen). There are also trace levels (< 0.1%) of other gases such as water vapour (210 ppm) and oxygen (0.15%). 

The other main difference in terms of the atmosphere is the pressure at the surface. At 610 Pa this is only 0.60% of the surface pressure on Earth, and as about 96% of this is CO₂, this means that there is a surface density of 3610 mol/m² of CO₂ on Mars compared to only 150 mol/m² on Earth. So any outgoing radiation from the surface of Mars has 24.06 times as much carbon dioxide gas to penetrate, in order to escape into outer space, compared to on Earth. What this means in practice is that the Greenhouse Effect in the Martian atmosphere should be easier to analyse because it can only have one source - CO₂.

 

The Energy Balance for Mars

Mars is also approximately 52% further from the Sun than is Earth, so one might expect that to mean that its surface is colder. This is true, but not as much as it should be based on distance alone. 

The solar radiation flux entering the Martian atmosphere is only 586 W/m² compared to the 1360 W/m² that irradiates the Earth. As this radiation is spread over a surface area (4πr²) that is four times greater than the cross-sectional area of the planet (πr²) in each case, this means that the average radiation flux at the Martian surface is 143.5 W/m². Yet this is only 22% less than the 184 W/m² that reaches the Earth's surface. This is because nearly 50% of incident radiation on Earth is either reflected by clouds or is absorbed by ozone and water vapour in the upper atmosphere. But there are no clouds, ozone or significant water vapour on Mars.

Then there is the issue of surface albedo or Bond albedo. This is the proportion of incident radiation that is reflected by the planet back out into space without being absorbed, either from clouds or the surface. For Earth this is about 31%; for Mars it is only 25%. This means that the average surface absorption on Mars is 108 W/m² compared to 161 W/m² on Earth. So while Mars only receives 43% of the solar radiation that Earth does, after absorption and reflection the Martian surface receives 67% of the radiation that the Earth's surface does. That is a relative increase of more than 50% for Mars which partially compensates for its greater distance from the Sun.

Calculating the Surface Temperature of Mars

If we now invoke the Stefan-Boltzmann law (see Eq. 13.1 in Post 13),

I = σT⁴

(89.1)

where I is the surface radiation flux, σ is the Stefan-Boltzmann constant, and T is the surface temperature in kelvins, we see that a surface radiation flux of 108 W/m² equates to a mean surface temperature on Mars of 209 K (or -64°C). Yet the true mean temperature is thought to be about 215 K (or -58°C). The difference is due to the Greenhouse Effect. 

For comparison, on Earth a solar flux at the surface of 161 W/m² would equate to a mean surface temperature of 231 K (or -42°C), yet the true mean temperature is about 289 K (or +16°C). So the GHE on Earth adds 58°C of warming while on Mars it only adds 6°C. Yet there is almost twenty-five times more carbon dioxide on Mars (3690 mol/m²) than on Earth (150 mol/m²), so you would expect the greenhouse effect due to CO₂ to be stronger. But how much stronger? The answer is: not very. In fact it is significantly less than the actual measured value on Earth.

Calculating the Strength of the GHE on Mars

In Post 87 I showed how the width of the CO₂ absorption band at 15 µm can be determined using the known concentration of CO₂ (N_o), its scattering or absorption cross-section (σ_s), the quantized frequency of rotation of the CO₂ molecules (B), and the temperature (T). From this it is possible to estimate the critical CO₂ concentration needed to absorb most of the infra-red radiation (N_th). The term N_th can be estimated to be 0.5 mol/m² based on the value of σ_s, while N_o will be about half the total CO₂ concentration, so N_o = 1845 mol/m². From this we can estimate the maximum number of excited rotational states in the absorption band, J_th, using (see Post 87)

(89.2)

where k is Boltzmann's constant, h is Planck's constant and Z is a normalization constant (see Eq. 87.2 in Post 87) equal to 185.5 in this case. The ratio term kT/hB has the value 185.3 (as hB = 0.1 meV and T = 215 K) and is always approximately equal to the Z value. 

The result we obtain is that J_th = 36.3, which, given that the spacing of the bands is 0.2 meV, means that the absorption band has a width of 14.52 meV and extends from a wavelength of 13.78 µm to 16.44 µm. This compares to a calculated range of 14.00 µm to 16.14 µm for the same band on Earth, although the measured width on Earth is actually found to be from about 13.35 µm to 17.35 µm. So even though the calculated width of the 15 µm absorption band for Mars is slightly larger than the equivalent for Earth, it is not significantly greater. But it is significantly less than the measured band width on Earth.

 

Fig. 89.1: The electromagnetic emission spectrum for the surface of Mars at a mean temperature of 215K (blue curve) together with the absorption profile due to CO₂ between 13.78 µm and 16.44 µm (red curve).

The impact of the high Martian atmospheric CO₂ concentration on the radiation feedback is demonstrated in Fig. 89.1 above. The red curve indicates the proportion of the outgoing infra-red radiation (blue curve) that is reflected by the CO₂ molecules and it amounts to f = 12.5%. This is slightly more than the 10% seen for the GHE due to backscattering from CO₂ on Earth (see Post 87) despite the absorption band being further from the peak in the emission spectrum due to the lower surface temperature on Mars.

Calculating the Temperature Rise

The radiation feedback of  f = 12.5% shown in Fig. 89.1 equates to a 14.3% increase in the surface radiation and also of T⁴ (because of Eq. 89.1), which then equates to a 3.4% increase in T. So if the initial surface temperature on Mars without the GHE was 209 K, the temperature with the GHE included will be 3.4% greater, or 216.1 K. This means that the temperature rise at the surface due to the Greenhouse Effect is expected to be 7.1 K, which is pretty close to the observed value of around 6 K (or 6°C). The reason for the small difference could be the limited availability of accurate Mars temperature data, or the uncertainty in the value of the CO₂ absorption cross-section, σ_s.

We know how much radiation from the Sun is arriving at Mars to high accuracy, but knowing how much is being absorbed by the planet surface is more difficult as this depends on an accurate measurement of the Bond albedo. However, conventional astronomical telescopes should be able to measure the reflected radiation to pretty good accuracy as well. That allows us to estimate the expected mean surface temperature without the GHE to fairly high precision. The problem is knowing what the actual surface temperature is with the GHE in operation. This is a difficult enough calculation to do on Earth where we have over 16,000 weather stations measuring the surface temperature on a daily basis, and numerous satellites in orbit. Sadly, none, or very little, of this exists for Mars.

So far in this blog post I have assumed a value of 215 K for the mean surface temperature of Mars, but some reports have put it as high as 225 K (or as low as 210 K). In which case Z = 194.15 and J_th = 37.0. This leads to a 15 µm band stretching from 13.76 µm to 16.47 µm, and a feedback factor of f = 13.0%. Under these circumstances the warming from the Greenhouse Effect increases slightly, but only to 7.7°C. 

 

A Comparison with Earth

For comparison, it is instructive to hypothecate the extent of warming on Earth if its atmosphere also contained 3690 mol/m² of CO₂. In that case Z = 249.3 and J_th = 41.6, which leads to a 15 µm band stretching from 13.62 µm to 16.67 µm, and a feedback factor of f = 14.1%. The resulting predicted temperature rise due to CO₂ would be 10.74 K, which is 3.26°C less than the 7.48°C rise currently predicted for Earth as was shown in Post 87). So a twenty-five fold increase in the CO₂ concentration would only result in a 3.26°C temperature increase, although as I showed in Post 87, masking by water vapour would probably reduce this by 75% to only 0.8°C. 

It is a point of note that the density of CO₂ molecules on Mars (3690 mol/m²) is more than double the combined density of all the greenhouse gases on Earth (1560 mol/m²), yet it results in a temperature rise of 5°C - 7°C that is almost ten times less than the 58°C observed for Earth. This is mainly because most of the GHE on Earth is due to water vapour as the width of the CO₂ absorption band is so much less than that for water vapour. Even increasing the concentration of CO₂ on Mars by a factor of twenty-five cannot appreciably change this.

Summary and Conclusions

What I hope I have shown in this post is that Mars is a good test bed for studying the Greenhouse Effect (GHE). Knowing only its albedo, the atmospheric concentration of CO₂, and the intensity of radiation arriving from the Sun, it is possible to accurately predict the temperature rise due to the Greenhouse Effect. This I have predicted to be about 7°C, in close agreement with the current estimate based on observational data (6°C). And this is despite the significant uncertainty over the true measured value of the mean surface temperature on Mars.

The reduced GHE on Mars relative to the Earth occurs despite its much higher (i.e. 24 times greater) atmospheric CO₂ concentration. This in turn suggests that the increasing levels of atmospheric CO₂ we are currently seeing on Earth will produce only slight temperature increases in the future. 

Yes, Mars has its own complicating factors. Heat retention on Mars is limited by the thin atmospheric blanket compared to Earth. This means that the planet does not retain heat very well, but conversely it means that the atmosphere will warm quickly when heated by the Sun. For this reason it may be better to consider Mars under direct solar illumination in daytime. Under these conditions the peak solar flux at the surface of Mars will be four times greater than stated above, or 432 W/m². This will equate to a peak surface temperature of 295 K (or +22°C). Yet the actual maximum temperature is reported to be around 303 K to 308 K (or +30°C to +35°C). So on this measure the warming from the Greenhouse Effect in daytime near the equator appears to be in the range 8°C to 13°C. Yet the predicted value based on a calculation of the width of the 15 µm absorption band is found to be 10.9°C, in other words in the mid-range of the observed values. Once again this is still much less than the total warming seen on Earth and comparable to the contribution to Earth's GHE seen just from CO₂.

87. How the Greenhouse Effect on Earth changes with increasing carbon dioxide concentration

In my previous post (Post 86) I explained how infra-red photons emitted by the Earth's surface interact with carbon dioxide (CO₂) in the atmosphere to create the Greenhouse Effect. I also showed that increasing the temperature of the planet and increasing the concentration of carbon dioxide in the atmosphere will both lead to an increase in the width of the 15 µm absorption band of CO₂. This in turn will increase the amount of radiation that is backscattered by the CO₂, and therefore increase the amount of radiation heating the surface of the planet. 

In this post I will attempt to quantify the temperature increase for different increases in the CO₂ content of the atmosphere using the results presented in Post 86 and Post 85. What I will show is that the increase in atmospheric levels of CO₂ from 280 ppm in 1750 to almost 420 ppm today can only be responsible for at most a 0.5°C increase in average temperatures. This is only about 40% of the 1.2°C claimed by the IPCC and climate scientists. In fact the actual temperature rise due to CO₂ is likely to be less than half the calculated value of 0.5°C due to the masking effects of water vapour, and could be as little as 0.1°C. To put this into context, this is less than the values I have calculated for urban heating effects from waste heat (see Post 14 and Post 29) which would persist even without the use of fossil fuels.

The maths and physics

The starting point for this analysis is the quantum structure of the absorption band. This is shown in Fig. 87.1 below and was discussed in detail in Post 86. The key issue is the height of the various absorption lines in the P and R branches. These are identified by their angular momentum quantum number, J, which is numbered for each branch from the centre of the band, Q. 

Fig. 87.1: The detailed structure of the 15 µm absorption band for CO₂ showing the absorption peaks associated with rotational transitions.

In Post 86 I also showed that the width of the 15 µm band is determined by the value of J that satisfies the following equation (see also Eq.86.9), this value being denoted as J_th.

(87.1)

In this equation T is the thermodynamic temperature in kelvins, k is the Boltzmann constant, h is Planck's constant and B is the frequency of the rotational angular momentum states. For the rotational transitions shown for CO₂ in Fig. 87.1, hB = 0.1 meV and is equal to half the energy separation of the lines in the spectrum in Fig. 87.1. The other terms will be explained below.

 

The Z term

The term Z is a normalization term equal to the total number of possible rotational states per molecule in the R (or P) branch as follows. 

(87.2)

 

In the case of Earth where the mean surface temperature T = 289 K, the term Z = 249.3. The energy term E_J = J(J+1)hB. As the degeneracy term (2J + 1) is the differential of the J component of the energy term J(J+1), it follows that for large T the summation in Eq. 87.2 reduces to an integral over all J states, in which case Z ≈ kT/hB.

 

 

The N_o term

 

The term N_o in Eq. 87.1 is equal to the total number of CO₂ molecules per unit surface area found in the R branch. This can be estimated as being equal to approximately half the molecules, with the other half being in the P branch which is assumed to be the mirror image of the R branch (but is not really as was explained in Post 86). This also neglects the significant number of CO₂ molecules (particularly at low temperatures) found in the Q peak. Nevertheless, this approach does at least set an upper limit to the width of the R branch, and thus the width of the 15 µm band as a whole. And as will be shown below, it does give results that are remarkably accurate. As the number of CO₂ molecules per unit surface area found on Earth is 150 moles per square metre, it therefore follows that N_o is equal to 75 mol/m².

Calculating N_th and J_th.

The final remaining parameter to calculate is N_th. Ideally, if the absorption band edge had vertical edges, it would be the threshold number of CO₂ molecules per unit area that are just sufficient to completely block the radiation and would be equal to the reciprocal of the scattering cross-section, σ_s. As σ_s for CO₂ molecules is estimated to be between 10^-24 m² and 10^-23 m² in the 15 µm band, that would imply a value for N_th of about 1 mol/m². In practice, however, the band edge is curved so the usual definition of the edge is to take the position of the half maximum. This means using a value of N_th = 0.5 mol/m² is more appropriate.

With all the parameters now set we can calculate J_th using Eq. 87.1 above. The result we get is 29.4, which when multiplied by the line spacing, 2hB, gives the width of the R branch as 47.4 cm^-1 in wavenumbers. Assuming the P branch is identical means that the 15 µm band will extend from 619.6 cm^-1 to 714.4 cm^-1, or from 14.00 µm to 16.14 µm. This is remarkably close to the 14.2 µm to 16.2 µm that is generally observed for the peak in the absorption.

Having calculated the width of the 15 µm band with an atmospheric CO₂ concentration of 420 ppm, we can also repeat the procedure for any other CO₂ concentration of our choosing. For example, an atmospheric CO₂ concentration of 280 ppm that is characteristic of global conditions in 1750 leads to a value for J_th of 27.3, which means that the width of the R branch would be 44.0 cm^-1.

The temperature rise

In Post 85 I showed how the reflection of a fraction f of outgoing infra-red radiation would reheat the Earth's surface and cause the radiation it absorbed to increase from I_o to a higher value I_T as follows

(87.3)

Then in Post 86 I showed how the width of the 15 µm absorption band could be used to determine the value of f by calculating the relative area of this band under the absorption spectrum (see Fig. 86.1). This can then be used to infer a temperature rise due to the absorption by utilizing the Stefan-Boltzmann law,

 I = σT⁴. 

(87.4)

If I_T is the intensity of radiation emitted by the Earth's surface normally (i.e. 396 W/m²), and f is the fraction of radiation reflected back by the CO₂, then the intensity of radiation emitted by the Earth's surface without the CO₂ greenhouse effect will, according to Eq. 87.3, be I_o = (1-f)I_T. We can then use Eq. 87.4 to calculate the respective surface temperatures T_f and T_o for each radiation emission intensity, I_T and I_o. The difference in the two temperatures will be the warming due to the CO₂.

I showed above that an atmospheric CO₂ concentration of 420 ppm leads to an absorption band that extends from 14.00 µm to 16.14 µm. Combining this with the black body spectrum of the Earth at T_f = 289 K (see Fig. 87.2 below) allows us to determine f to be f = 10.0%. This in turn implies that I_o = 356.1 W/m² (where I_o is the radiation intensity without CO₂ feedback), and thus T_o = 281.52 K. So the temperature rise due to CO₂ is 7.48 K.

 

Fig. 87.2: The electromagnetic emission spectrum for the Earth's surface at a mean temperature of 289K (blue curve) together with the absorption profile due to CO₂ between 14.00 µm and 16.14 µm (red curve).

Now if we reverse this calculation but use an atmospheric CO₂ concentration of 280 ppm, we find that the absorption band now extends from 14.06 µm to 16.05 µm, so f = 9.28%. The value of I_o = 356.1 W/m² will be the same as before but the addition of a different amount of CO₂ will change I_T and T_f because f is different. The new values will be I_T = 392.6 W/m² and T_f = 288.46 K. So the temperature rise from CO₂ is now only 6.94 K. This implies that the temperature rise since 1750 due to the atmospheric CO₂ concentration increasing from 280 ppm to 420 ppm is only 0.54°C (i.e. 7.48°C - 6.94°C). 

If we repeat this process for other past or future (potentially) CO₂ concentrations we can calculate a theoretical temperature rise for each. This is shown in the graph in Fig. 87.3 below with the temperature changes all measured relative to the 1750 value when the atmospheric CO₂ concentration was 280 ppm.

 

Fig. 87.3: The theoretical effect of an increasing atmospheric CO₂ concentration on the contribution of CO₂ to global warming.

What Fig. 87.3 demonstrates is that the expected temperature increase from an increase in atmospheric CO₂ has a logarithmic dependence on the CO₂ concentration. However, the trend for concentrations between 280 ppm and 420 ppm is fairly linear and leads to a 0.5°C increase. Overall it appears that doubling the CO₂ concentration leads to about 1°C (or 1 K) of warming.

The interpretation of the data

While the logarithmic trend shown in Fig. 87.3 is in general agreement with climate models, the magnitude of the temperature changes are not. Whereas Fig. 87.3 suggests that 420 ppm of CO₂ leads to about 0.52°C of warming, the IPCC and climate science are claiming the rise is much greater at about 1.2°C. The difference, I suspect, is probably down to the impact of water vapour. Unfortunately, there are many ways that water vapour can impact the temperature trend.

The conventional view from climate scientists is that water vapour is a positive amplifier; the theory being that a warmer climate causes the amount of water vapour in the troposphere to increase, thus creating even more warming. As I pointed out in Post 86, the total feedback factor for infra-red radiation, f, is about 59%, while CO₂ alone can only account for about 18%, assuming that the 15 µm CO₂ absorption band width is measured at its half-maximum points from 13.35 µm to 17.35 µm. So the assumption is that water vapour is responsible for the rest, and that as its atmospheric concentration is dependent on the temperature, its concentration will increase as the level of CO₂ increases. So this will make the feedback, f, increase about three times faster than from CO₂ alone and so massively increase the temperature change to 1.2°C. The problem with this theory is that it ignores two major snags. 

First, the 15 µm CO₂ absorption band overlaps with the H₂O absorption band, as shown in Fig. 87.4 below. At the high wavelength edge of the 15 µm CO₂ band (17 µm) the water vapour will absorb almost 100% of the outgoing radiation while at the low wavelength edge (13 µm) it will absorb about 50%. This means that about 75% of any increase in the width of the 15 µm CO₂ absorption band will be masked from the outgoing radiation by the water vapour. In which case the temperature rise will only be 25% of the predicted value, or about 0.13°C.

 

Fig. 87.4: The absorption bands of carbon dioxide and water vapour at sea level.

Secondly, the window in the H₂O absorption band extends from 8 µm to about 15 µm (using the half maxima points). This window allows only 41% of the Earth's outgoing infra-red radiation to escape. As we know that the feedback factor f = 59%, this means that water vapour could be responsible for absorbing and reflecting almost all the outgoing infra-red radiation that is absorbed and reflected. In other words, the 15 µm CO₂ band is not needed, and in fact is probably, largely redundant because it is hiding behind the water vapour. So again, a small change to the width of the CO₂ band is unlikely to cause any major temperature changes. This is why so many eminent physicists have so many serious reservations regarding the global warming predictions coming out of climate science.

 

The conclusions

1) Increasing the atmospheric CO₂ concentration will increase the width of its 15 µm absorption band.

2) In the absence of water vapour this could raise global temperatures, with an increase in CO₂ concentration from 280 ppm to 420 ppm resulting in a 0.5°C increase in global temperatures. 

3) The projected temperature increase has a logarithmic dependence on CO₂ concentration (see Fig. 87.3).

4) Water vapour masks most of the CO₂ 15 µm absorption band and so dominates the infra-red absorption. It can also account for almost all of the radiation feedback on its own.

5) The impact of water vapour means that an atmospheric CO₂ concentration rising from 280 ppm to 420 ppm could result in as little as a 0.13°C increase in global temperatures. This is ten times less than is currently claimed by climate science.

The caveats and discrepancies

In this analysis there are major uncertainties over the value of the CO₂ scattering cross-section, σ_s, and the widths of the CO₂ and H₂O absorption bands. This is also due to the difficulty in estimating the parameters N_o, N_th and J_th. However, the overall level of agreement between this analysis and real data and existing theory is encouraging.

The major discrepancy is between the measured width of the CO₂ 15 µm absorption band at its half maximum, where it extends from 13.35 µm to 17.35 µm, with the predicted width based on J_th where it extends from 14.00 µm to 16.14 µm. This difference could be due to line broadening from pressure broadening and temperature.

85. The Greenhouse Effect

In the overall debate over global warming probably the most contentious area for many is the scientific validity of The Greenhouse Effect. Whether on Twitter or on climate sceptic sites like WUWT, there are many commenters who simply refuse to accept it, or fail to understand it. In fact many climate scientists (particularly non-physicists) also do not fully understand it, or misrepresent it. In this post I will outline some of the common misconceptions about it, and then explain how the greenhouse effect actually arises. 

 

Myth 1: Carbon dioxide causes an increased heating of the atmosphere

As the atmosphere can absorb heat that is radiated from the surface of the planet, the claim here is that the presence of greenhouse gases like carbon dioxide (CO₂) increases the amount of heat that the atmosphere can store. This is true(ish), but the amount of additional heat or thermal energy stored by CO₂ is so small relative to the total that it is irrelevant.

The key property here is the molar heat capacity of the gas. Every gas in the atmosphere has a different heat capacity, this being the additional amount of thermal energy stored in that gas per unit increase in temperature. However, they are generally very similar in magnitude (see here), although the molar heat capacity of CO₂ is about 25% greater those of nitrogen (N₂) and oxygen (O₂) due to its additional degrees of freedom in accordance with the equipartition theorem. But carbon dioxide only comprises about 0.042% of all the molecules in the atmosphere, so it can only increase the total heat capacity of the atmosphere by an insignificant 0.01%. But more importantly, even this small increase is irrelevant because it is the temperature of the atmosphere that determines its rate of thermal emission, not the quantity of heat that it stores. 

The amount of heat stored merely determines the rate at which the atmosphere will cool at night. This is why planets with thick atmospheres, like the Earth and Venus, cool less at night than planets with thin atmospheres like Mars. Their thick atmospheres mean that they store a lot more energy at a given temperature, but it is the temperature that determines the rate of energy loss. So two planets at the same temperature will cool at different rates if they have different densities of atmosphere, even though the initial rate of energy loss (as set by the temperature and the Stefan-Boltzmann law) will be the same for each. This is because the planet with the thinner atmosphere will run out of stored energy first.

Myth 2: The greenhouse effect is the result of a hot atmosphere heating the Earth's surface

This myth is related to, and dependent on, Myth 1. If the atmosphere is getting hotter because the CO₂ is trapping and storing heat emitted by the Earth's surface, then the temperature of the atmosphere will increase. Eventually the atmosphere will become hotter than the surface and so it will begin reheating the surface. So the surface temperature will also increase. Except this is not how greenhouse gases work. 

They don't trap heat for long periods, but instead just reflect it back to the surface. In essence they behave like a thermal mirror. The result is that the surface gets reheated by the atmosphere, but not because the atmosphere is hotter than the surface. The lower atmosphere, or troposphere, is never hotter than the surface. It is just that the photons of infra-red radiation emitted by the surface bounce off the CO₂ molecules, and some then get reflected back to the surface and reheat it.

Myth 3: Thermal radiation cannot move from a cold object to a hotter one

One reason many climate sceptics appear to reject the concept of the greenhouse effect is that they feel it violates basic principles of physics, not least the second law of thermodynamics. One of the many versions of this law states that net heat flow is always from a hot object to a cooler one, and not in the reverse direction. Many thus misinterpret this law because they fail to appreciate the importance of the term "net". It is not that heat or thermal energy cannot flow from a cold object to a hotter one: it does. In fact all objects emit (and absorb) thermal radiation irrespective of their temperature; the Stefan-Boltzmann law tells us that (see Post 12). The key point is that hotter objects emit more. In fact the Stefan-Boltzmann law dictates that the amount of radiation emitted is proportional to the fourth power of the thermodynamic temperature T measured in kelvins (see Eq. 12.6 in Post 12).

What the greenhouse effect does is increase the amount of energy that moves in the opposite direction by enabling the atmosphere to reflect back energy emitted by the surface. But the amount reflected back is always less than 100% of that emitted by the surface, so this still means that more energy is moving from the surface up into the atmosphere than is moving in the opposite direction. Thus, the net heat flow is still upwards into the atmosphere, moving from hot to cold. Consequently the second law of thermodynamics still holds.

Myth 4: There is too little carbon dioxide in the atmosphere to make a difference

Currently the concentration of carbon dioxide in the atmosphere is about 420 ppm, or 0.042% of all the gas molecules. This looks like a small number, but there are a lot of molecules in the atmosphere. In fact there are are 0.357 million moles of gas for every square metre of the Earth's surface (1 mole = 6.02 x 10²³ atoms or molecules). So 0.042% of that equates to 150 moles of carbon dioxide per square metre, or 9.04 x 10²⁵ molecules of carbon dioxide per square metre. 

As these molecules are typically 0.33 nm in diameter, this still means that every infra-red photon emitted from the surface of the Earth will expect to collide with at least ten million CO₂ molecules before it can escape into outer space. Sooner or later one of these molecules with absorb it and then re-emit it, and half of these re-emissions will be in a reverse direction towards the Earth's surface. That is why so few infra-red photons can escape. 

The exact number of collisions depends on the scattering cross-section of the molecule at the relevant wavelength of radiation. This cross-section represents the effective area of the molecule that the photon of radiation sees, or alternatively the actual area of the molecule multiplied by the probability of being absorbed at each potential collision. So while the actual cross-sectional area of the carbon dioxide molecule is about 10^-19 m², the effective area as measured by spectroscopy is much less, around 4x10^-24 m². This means that the number of collisions each photon can expect to make with a CO₂ molecule before it can escape into outer space is only about 360 (i.e. 9.04 x 10²⁵ x 4 x 10^-24). 

This, though, is still more than enough to block the emission path of virtually every photon with the necessary wavelength. In fact most will be blocked within 30 m of the surface (the result of dividing the effective thickness of the atmosphere of 10 km by 360). But as Fig. 85.1 below shows, only photons with wavelengths close to the CO₂ absoption bands at 2 µm, 2.7 µm, 4 µm and 15 µm can be absorbed by the carbon dioxide. For the rest the CO₂ molecules will be completely transparent.

Fig. 85.1: The absorption spectrum of different greenhouse gases in the visible and infra-red.

How the greenhouse effect really works

The starting point is electromagnetic radiation from the Sun which heats up the surface of the planet. As the surface warms it also gives off radiation, but because the temperature of the Earth's surface (288 K) is much less than that of the Sun (5778 K), the energy, or frequency, of the radiation emitted is much less than that of the incoming radiation. That means that its wavelength is longer - typically about twenty times greater. So while the incoming radiation from the Sun is mainly in the visible part of the electromagnetic spectrum (see the red curve in Fig. 85.1), the radiation emitted by the Earth's surface is generally in the infra-red (see the blue curve in Fig. 85.1).

The effect of greenhouse gases like carbon dioxide is to reflect back some of the outgoing infra-red radiation. This then gets re-absorbed by the surface and heats it further. This is the greenhouse effect. The key point is that the outgoing radiation is merely being reflected back by collisions with carbon dioxide (or water) molecules in the atmosphere. So these greenhouse gas molecules act like a mirror. In the next post I will outline the mechanism and mathematics of this in more detail. Any additional heating of the atmosphere only comes later as a result of the additional heating of the surface.

The result of this reflection of outgoing radiation is that the amount of radiation hitting the Earth's surface and being absorbed increases. For example, suppose the amount of radiation from the Sun that is being absorbed by the Earth's surface is I_o. As I showed in Post 13 (The Earth's energy budget) this equates to about 161 W/m². With no greenhouse effect in place the outgoing radiation will balance the incoming radiation, and so according to the Stefan-Boltzmann law (see Eq. 12.6 in Post 12) the surface temperature will be 231 K (or -42°C). 

However, if a fraction p of the initial outgoing radiation is reflected back (i.e. pI_o), then the total incoming radiation will be (1 + p)I_o . This will heat up the surface even more and result in a higher emission temperature, which in turn will increase the total intensity of the outgoing radiation I_T. If we then assume that the greenhouse gases reflect back a fraction f of the outgoing radiation, then the following equation must hold. 

(85.1)

This basically states that the total outgoing radiation must balance the incoming radiation plus the fraction of the outgoing radiation that is reflected back I_r = f I_T. Rearranging Eq. 85.1 gives the result

(85.2)

We know that the current mean surface temperature of the Earth is approximately 289 K (or 16°C), so this allows us to calculate I_T using the Stefan-Boltzmann law

I = σT⁴

(85.3)

where T is the temperature in kelvins and σ is the Stefan-Boltzmann constant. The result we obtain is that I_T = 396 W/m², and as I_o = 161W/m², this then implies that f = 0.59. In other words, the greenhouse gases reflect back about 59% of all outgoing infra-red radiation. 

Knowing the values of I_T and I_o also allows us to use Eq. 85.3 to determine the temperature of the Earth's surface both with and without the reflected radiation. These values will be 289 K and 231 K respectively. So the reflected radiation due to the Greenhouse Effect has increased the Earth's temperature by 58 K.

13. The Earth's energy budget

In order to understand how the Earth is heating up, you need to understand why it is warm in the first place. That means you need to know where the energy is coming from and where it is going. That is the basis of the Earth's energy budget or energy balance.

The purpose of this post is to analyse that energy balance, and to determine which parts of it can change, and what the effects of those changes are likely to be. Specifically, this post will try to relate various possible changes in the energy balance to any consequential changes in global temperatures. In so doing, it will also be necessary to critically ascertain the degree of confidence that there is surrounding the various estimates, and measurements, regarding the energy flows in the different parts of the atmosphere.

As I pointed out in the last post, virtually all the energy that is present on Earth originated in the Sun. The amount of energy per second arriving from the Sun at the top of the Earth’s atmosphere is 1361 watts per square metre (W/m²), and as I also pointed out, because the area this energy is ultimately required to heat up (4πr² where r is the Earth's radius) is four times the cross-sectional area that actually captures the energy (πr²), that means that the mean power density (remember: power is rate of flow of energy) that the Earth receives is only a quarter of the incoming 1361 W/m², or about 341 W/m². However as I also showed in Fig. 12.1, not all this energy reaches the Earth's surface. In fact only about 161 W/m² does. The rest is either absorbed by the atmosphere (78 W/m²), reflected by the atmosphere and clouds (79 W/m²), or is reflected by the Earth's surface (23 W/m²). This is shown diagrammatically in Fig. 13.1 below.

  

Fig. 13.1: The Earth's energy budget as postulated by Trenberth et al. (2009).

The image in Fig. 13.1 is taken from a 2009 paper by Kevin Trenberth, John Fasullo and Jeffrey Kiehl (Bull. Amer. Meteor. Soc. 90 (3): 311–324). It is not necessarily the most definitive representation of the energy flows (as we shall see there are other models and significant disparaties and uncertainties in the numbers), but it is probably the most cited. The data it quotes specifically relates to the energy budget for the period March 2000 - May 2004.

Fig. 13.2: The Earth's energy budget as postulated by Kiehl and Trenberth (1997).

The 2009 Trenberth paper is not the first or last paper he has produced on the subject. The energy budget it describes is actually a revision of an earlier attempt from 1997 (J. T. Kiehl and K. E. Trenberth, Bull. Amer. Meteor. Soc., 78, 197–208) shown in Fig 13.2 above, and has since been revised again in 2012 (K. E. Trenberth and J. T.  Fasullo, Surv. Geophys. 33, 413–426) as shown in Fig. 13.3 below.

Fig. 13.3: The Earth's energy budget as postulated by Trenberth and Fasullo (2012).

The only real difference between the energy budget in Fig. 13.3 and that from 2009 in Fig. 13.1 is the magnitude of the atmospheric window for long wave infra-red radiation (revised down from 40 W/m² to 22 W/m²), but I still think this highlights the level of uncertainty that there is regarding these numbers. This is further emphasised by a contemporary paper from Stephens et al. (Nature Geoscience 5, 691–696 (2012) ) shown below in Fig. 13.4.

Fig. 13.4: The Earth's energy budget as postulated by Graeme L. Stephens et al. (2012).

As the 2009 Trenberth paper appears to be the most cited it is probably best to use this as the basis for the following discussion, but to bear in mind the amount of uncertainty regarding the actual numbers.

In Fig. 13.1 the three most significant numbers are those for the direct surface absorption from the Sun (161 W/m²), the upward surface radiation (396 W/m²), and the long-wave infra-red back radiation due to the Greenhouse Effect (333 W/m²). Of these it is the upward surface radiation (396 W/m²) that determines the temperature but its value is set by the other two.

As I explained in the last post the emission of electromagnetic radiation from a hot object is governed by the Stefan-Boltzmann law as shown below

  

(13.1)

where I(T) is the power density (per unit area) of the emitted radiation, σ = 5.67 x 10^-8 Wm^-2K^-4 is the Stefan-Boltzmann constant, and the term ε is the relative emissivity of the object. The emissivity defines the proportion of the emission from that object at that wavelength compared to a black body at the same temperature, and it varies with wavelength. It is also different for different materials. In the case of planet Earth, it is generally assumed to be very close to unity all over the surface for all emission wavelengths, but this is not always the case.

It is Eq. 13.1 that allows us to determine the surface temperature (T = 289 K) from the upward surface radiation (396 W/m²) or visa versa. It also allows us to calculate the change in upward surface radiation that would result from a given increase in the surface temperature. It turns out that an increase in surface temperature of 1 °C would necessitate the upward surface radiation increasing from 396 W/m² to 401 W/m², in other words a 1.39% increase. A 2 °C increase would require a 2.80% increase in the upward surface radiation.

I also explained in the last post how the total upward surface radiation (I_T) was related to the direct surface absorption from the Sun (I_o) via a feedback factor f which represented the fraction of upward surface radiation that was reflected back via the Greenhouse Effect.

(13.2)

This model assumed that all the energy absorbed by the greenhouse gases came from one source, though, namely surface upward radiation, and was driven by a single input, the surface absorption of solar radiation, I_o. As Fig. 13.1 indicates, this is not the case. This means that Eq. 13.2 will need to be modified.

The aim here is to determine what changes to the energy flows in Fig. 13.1 would result in a particular temperature rise, specifically a rise of 1 °C in the surface temperature. Realistically, there are only three things that could bring about any significant change. The first is a change in the amount of energy coming from the Sun. The second is is a change in the direct absorption of radiation at the surface, I_o. The third is a change in the strength of the Greenhouse Effect, f.


Case 1: Changes to the incoming solar radiation.

This is probably the easiest of the three propositions to analyse. If the incoming solar radiation at the top of the atmosphere were to change by 1.39%, then we would expect virtually all the projected heat flows in Fig. 13.1 to change by the same amount, including the upward surface radiation (from 396 W/m² to 401 W/m²). This is because almost all the scattering mechanisms and absorption processes in Fig. 13.1 are linear and proportional. The two exceptions are likely to be the thermals (17 W/m²) and the evapo-transpiration (80 W/m²), the former of which will be governed more by temperature differences, and the latter by the non-linear Clausius-Clapeyron equation. While changes to these two components are likely to be linear for small changes, they are unlikely to be proportional. However, as the changes to these two components are likely to be fairly small and comparable to other errors, we can probably ignore these deficiencies. So, if the incoming solar radiation (1361 W/m²) were to increase by 1.39% we could see a global temperature rise of 1 °C.

The problem is that there is no evidence to suggest the Sun's solar output has changed by anything like 1.39% over the last 100 years, and no obvious theoretical mechanism to suggest that it could. The only evidence of change is from satellite measurements over the last 40 years or so that suggest an oscillation in solar output with an eleven year period and an amplitude of about 0.05% (see Fig. 13.5 below). This would give a maximum temperature change of about 0.1 °C.

Fig. 13.5: Changes in the Sun's output since 1979 (from NOAA).

The only other known mechanism is the Milankovitch cycle. This can produce temperature oscillations of over 10 °C in magnitude (peak to trough) but is only seen over 120,000 year cycles (see red curve in Fig. 13.6 below). 

Fig. 13.6: Changes to temperature in the southern oceans (red curve) derived from isotope analysis of the Vostok ice core in Antarctica.

These temperature oscillations are mainly due to changes in the Earth's orbit around the Sun (changes to a more elliptical ortbit), or changes in the Earth's angle of inclination or tilt, or an increased precession that then exposes the polar regions to higher levels of solar radiation. Such effects may be responsible for the cycle of ice ages, but cannot be responsible for changes thought to have happened over the last 100 years. As the data in Fig. 13.6 indicates, even the periods of fastest climate change amounted to only a 10 °C increase over 10,000 years, or 0.1 °C per century, and we do not appear to be in one of those warming periods. If anything, the planet should be slowly cooling by about 0.01 °C per century.

The conclusion, therefore, is that global temperatures may fluctuate by 0.1 °C across the decade due to changes in solar output, but there is no evidence or credible mechanism that would support a long-term warming trend.


Case 2: Changes to the direct absorption of radiation at the surface.

The second possible driver of global warming comes from changes at the surface, specifically to the thermal energy absorbed there, I_o. This will then impact on the total upward surface radiation I_T and thereby also on the back radiation. According to Eq. 13.2 the changes to I_o and I_T should be proportional. As Eq. 13.1 indicates that a 1 °C change to the surface temperature, T_o, should result in a 1.39% change to I_T, it follows that a 1.39% change to I_o should result in a 1 °C change to T_o. Unfortunately there are three additional complications that we need to consider: the thermals (I_th = 17 W/m²), the evapo-transpiration (I_E = 80 W/m²), and the incoming solar radiation absorbed by the atmosphere (I_A = 78 W/m²).

The thermals (17 W/m²) and evapo-transpiration (80 W/m²) in Fig. 13.1 transfer heat from the surface into the upper atmosphere (top of the tropopause) by mass transfer (convection) rather than radiation. This may potentially provide a route for heat to escape from the Earth via a by-passing of the greenhouse mechanism. However, I would expect this energy to eventually get dumped in the atmosphere somewhere before the top of the tropopause (at a height of 20 km). When this happens it will merely add to the long-wave infra-red radiation being emitted from the surface, and so should still be reflected by the greenhouse gases. So while these heat sources will not contribute to the surface temperature as defined in Eq. 13.1, they should be included in the feedback factor f in Eq. 13.2.

So too will some of the power absorbed by the atmosphere directly from the incoming solar radiation (78 W/m²). Here again things are complicated because if the energy is absorbed before the bottom of the stratosphere (at 20 km altitude), the Greenhouse Effect will actually reflect some of that heat back into space. To account for this we can include an additional parameter μ as a variable that specifies the proportion of the incoming solar absorbed by the atmosphere that is absorbed in the lower atmosphere where it can be reflected backwards the surface. The fraction (1-μ) absorbed in the upper atmosphere will escape and therefore will not contribute to the back radiation.

In all there are seven energy terms that we need to consider.

1. Initial surface absorption (I_o = 161 W/m²).
2. Thermals (I_th = 17 W/m²).
3. Evapo-transpiration (I_E = 80 W/m²).
4. Upward surface long-wavelength radiation (I_up = 396 W/m²).
5. Long-wavelength back radiation (I_RF = 333 W/m²).
6. Incoming solar absorbed by the atmosphere (I_A = 78 W/m²).
7. Net radiation permanently absorbed by the Earth's surface (I_net = 0.9 W/m²).

We must then consider energy conservation at the surface and in the atmosphere. At the surface the law of conservation of energy (1st law of thermodynamics) requires that

 (13.3)

while in the atmosphere similar considerations mean that the total energy entering the atmosphere must equal the total that is emitted. As f is the proportion that is reflected back it follows that

(13.4)

The parameter μ is a variable that specifies the proportion of the incoming solar absorbed by the atmosphere (I_A) that is absorbed in the lower atmosphere where it can be reflected back towards the surface. The fraction (1-μ) absorbed in the upper atmosphere will escape and therefore will not contribute to I_RF. It therefore follows that

(13.5)

Using Eq. 13.5 we can work out a value for f, but only if we know μ, which we don't. However, using Eq. 13.4 and the knowlege that μ must lie in the range 0 <  μ < 1, we can say that f will be in the range 0.583 to 0.675 and that when μ = 0.5, f = 0.626. This allows us to estimate the change required in I_o to generate a 1 °C change in T_o, but to do that we will need to make some assumptions given the number of variables that there are.

First we can probably assume that f, μ and I_A remain unchanged even when I_o changes. We know that a 1 °C increase in T_o will result in a 1.39% increase in I_up to 401.5 W/m² and a 2 °C increase in T_o will result in a 2.80% increase in I_up to 407.1 W/m². The question is what happens to the thermals (I_th), the evapo-transpiration (I_E) and the net surface absorption (I_net)? They will probably increase as well, but by how much? A good starting point is to assume that they will increase by the same percentage as the upward surface long-wavelength radiation (I_up). A benchmark control is to assume that they stay constant. This gives us the following two scenarios.

If I_th, I_E and I_net scale with I_up and the scaling factor due to the increase in temperature T_o is g, then Eq. 13.5 can be rearranged to give

(13.6)

whereas if I_th, I_E and I_net are constant then

(13.7)

We know that g = 1.0139 for a 1 °C rise in T_o and g = 1.0280 for a 2 °C rise in T_o. So combining the two options in Eq. 13.56 and Eq. 13.7 implies that I_o is in the range 162.8-163.9 W/m². That implies an excess direct heating at the surface of ∆I_o = 2.33 ± 0.54 W/m², with the error range being set by the range of possible values for f, μ, I_E, I_net and I_th. A 2 °C increase in surface temperature would require a change in direct heating at the surface of ∆I_o = 4.69 ± 1.09 W/m².

The conclusion, therefore, is that a 1 °C increase in global temperatures would require an increase in the initial surface absorption of ∆I_o = 2.3 ± 0.5 W/m². How this might be achieved will be explored further in the next post.


Case 3: Changes to the feedback factor.

The most obvious and heavily reported mechanism by which global temperatures could increase is via changes to the Greenhouse Effect due to increased carbon dioxide concentrations in the atmosphere. The specific change that will ensue will be in the value of the feedback term, f, and hence the value of the back radiation, I_RF. As in the previous case, some of the heat flow parameters in Fig. 13.1 would change and some would stay the same. For example, we can confidently assume that I_A and I_o will remain unchanged, but if f changes, so might μ. But as before, the main question is what happens to the thermals (I_th) and the evapo-transpiration (I_E)?

Rearranging Eq. 13.5 once more gives

 (13.8)

while for the case that I_th, I_E and I_net are constant we get

 (13.9)

It turns out there is very little difference in the results using the two methods. The biggest factor affecting f is the value of μ. When there is no warming (g = 1.0) f = 0.629. A warming of 1 °C (g = 1.0139) requires f to increase to 0.634, and a warming of 2 °C (g = 1.0280) requires f to increase to 0.638. These values all correspond to values for μ of 0.5, but the possible spread of values for μ leads to an error in f of ±0.047 in all cases.

What this shows is that the increase in feedback factor needed for a 1 °C rise in global temperatures will be about 0.005. This is a small change, but at the end of the last post (Post 12) I calculated that the fraction of the long-wave infra-red radiation that could be absorbed and reflected by the carbon dioxide in its main absorption band (the frequency range 620-720 wavenumbers or the wavelength range 13.89 - 16.13 μm). The result was at best 10.5%. This implies that only about 15% of the Greenhouse Effect is due to CO₂, and the rest is due to other agents, mainly water vapour.

The conclusion, therefore, is that a 1 °C increase in global temperatures would require an increase in the width or strength of the carbon dioxide absorption band by at least 5% relative to its current size in order achieve this temperature rise.


The final point to note is the size of the potential measurement errors in the various energy flows, and the effect of rounding errors. A particular egregious anomaly occurs at the top of the atmosphere in Fig. 13.1 (and remains uncorrected in Fig. 13.3) where the rounded value of the incoming solar (341 W/m²) radiation balances the rounded outgoing values (239 W/m² and 102 W/m²). This is inconsistent with the rest of the diagram as there should be a 0.9 W/m² difference to account for the net absorption at the surface. In the more exact values quoted (341.3 W/m², 238.5 W/m² and 101.9 W/m²) this difference is specified correctly. So the problem is a rounding issue initially, but it then has a knock-on effect for the values quoted within the atmosphere.

For consistency it would therefore be better in this instance to round the 238.5 W/m² value down (to 238 W/m²) rather than up (to 239 W/m²). That would ensure that there was a net inflow of about 1 W/m² that balanced the net absorbed value at the surface (0.9 W/m²). It would also eliminate the false imbalance within the atmosphere itself. Here the net inflow should balance the net outflow (currently there is a 1 W/m² deficit). There can be no 0.9 W/m² energy gain in the atmosphere otherwise the atmosphere would heat up, and heat up by more than 2.7 °C per annum. What should remain invariant at various points from the surface to the top of the atmosphere is the following energy balance

(13.10)

where I_TOA = 238.5 W/m² is the outgoing long-wave radiation at the top of the atmosphere. A correction for this error requires the stated value for the power emitted upwards by the atmosphere (169 W/m²) in Fig. 13.1 to be reduced to 168 W/m².

It is also important to note that some of the errors in the energy flows in Fig. 13.1-Fig.13.4 are considerable, either in magnitude, or as a percentage. A comparison of the data in Fig. 13.1 and Fig. 13.4 illustrates how variable the results can be. The back radiation values, for example, do not agree within the noted error range, and the net surface absorption is 50% higher in Trenberth's papers than it is in the Stephens paper (Fig. 13.4). I shall look at the net surface absorption in more detail later as it has important implications for sea level rise, but the fact that this value is so small, not just relative to the other energy flows, but also in comparison to their errors, is a cause for concern with respect to its own accuracy. It should also be noted that the net surface absorption should also be measurable directly at the top of the atmosphere using satellite technology to measure both the solar energy going in and the Earth's thermal energy flowing out. Yet the discrepancies seen there between incoming and outgoing energy flows currently far exceed 0.9 W/m². The result is that most of the energy flows shown in Fig. 13.1-Fig.13.4 are at best estimates, and are often based more on climate models than on actual data.