27. Scaling of temperature anomalies for Australia

In my analysis of temperature data from both New Zealand (Posts 6-10) and Australia (Posts 18-21) I have speculated about the nature of the temperature fluctuations. These fluctuations have not behaved like normal white noise. For a start, when data from multiple stations are averaged, the standard deviation of the fluctuations barely changes. If the fluctuations behaved like white noise then the standard deviation would be expected to decrease by a factor of √N, where N is the number of stations in the average. This does not happen.

Then there is the scaling behaviour. If the data is smoothed with a moving average of length N points, again you would normally expect to see the standard deviation of the smoothed data decrease by a factor of √N compared to the unsmoothed data. Again this does not happen. The standard deviation decreases, but generally only by about a factor of N ^0.25. This is important because it essentially predicts how big the fluctuations will be for longer temperature records where each data points represents a longer time interval, such as yearly or decadal averages, rather than the monthly averages that form the basic station records I have been discussing here.

So what do we see for the mean temperature for Australia that I presented in Fig. 26.1 in the last post? In the following discussion I have restricted the analysis to data over a 140 year period from 1874 to 2013. This is because data earlier than this is derived by averaging over much less than 7 states, and will also be based on a much smaller number of individual stations.

Well, firstly the standard deviation of the data in Fig. 26.1 is only 0.627 °C. This is significantly less than that seen in individual temperature records, and in individual states like New South Wales where the value was 1.07 °C. The reason for this decrease is that the temperature record for Australia involves combining records from across the country, and the country is very big. It is, for example over 3600 km from Perth to Brisbane. Yet in Post 11 I showed that the correlation between monthly temperature records for stations that are spatially separated decreases almost linearly with the distance of separation (see Eq. 11.1). In fact, once you get to separations of more than 3000 km, the data in Fig. 11.2(a) suggest station records become completely uncorrelated. This is what appears to be happening here.

The monthly temperature data from Western Australia and Queensland will be almost totally uncorrelated as most of their respective stations are over 3000 km apart. So averaging the two will reduce the standard deviation by a factor of almost √2. Including the other states in the average could increase the reduction factor to √7, but this will be mitigated by the fact that the distances between those states are much less and so their correlations will be greater. The net result is a compromise with the standard deviation appearing to decrease by about 40% compared to the individual state values.

The second point to note is that the fluctuations in the mean temperature for Australia in Fig. 26.1 appear to conform to a Gaussian noise spectrum. This is confirmed below in Fig. 27.1.

Fig. 27.1: The distribution of anomaly values for the mean temperature record for Australia (blue curve), together with the predicted Gaussian distribution for a standard deviation of 0.627 °C.

However, these fluctuations are not white noise. If we smooth the data with different moving averages of size N months, and then recalculate the standard deviation, we get the data shown in Fig. 27.2 below. This is the scaling behaviour I described in the second paragraph above. For a more detailed explanation of its methodology, see Post 17.

Fig. 27.2: The change in standard deviation of the mean temperature anomaly for Australia (see Fig. 26.1) after smoothing with a moving average of size N. The gradient of the best fit line is -0.256 ± 0.003 and R² = 0.9993

The two significant features of the data in Fig. 27.2 are the gradient of the linear regression best fit line and the magnitude of the residual for the data relative to that line. The gradient is -0.256 ± 0.003 while the rms (root mean square) residual is 2.7% of the standard deviation of the y-values, the residuals being the vertical distance from the data point to the best fit line. This gives a value for R² of 0.9993, indicating a very good fit to the data.

The rms residual of 2.7% is incredibly low compared to previously determined values for individual states, while the gradient is incredibly close to -1/4. These two results may not be coincidental, and hint at the existence of a fundamental truth within the data, that these temperature records are fractal in nature, with the patterns of fluctuations over different timescales exhibiting strong self-similarity. If so, then this implies even 100-year mean temperatures would exhibit fluctuations with a standard deviation of over 0.1 °C and a range of over 0.4 °C. It would also suggest that changes of more than 0.5 °C in the average temperature of different centuries would be commonplace over the course of millenia. It should be noted that the data in Fig. 26.1 in the last post indicates that the average temperature in Australia over the whole of the 20th century was actually 0.063 °C less than that for the last 50 years of the 19th century.

So, are all the instrumental temperature records and their averages fractals? Do they exhibit self-similarity with a fractal dimension of 0.25 as I have suggested previously? Or is the data just white noise on an oscillating background as the data from South Australia might suggest? The answer is, it is too early to tell. We need more data and longer datasets. What we can say is that the temperature trend for Australia since 1853 in Fig. 26.1 is not a simple hockey stick.

26. The temperature trend in Australia since 1853 - PARABOLIC

In Posts 18-24 I calculated the temperature trend for each Australian state using all the available instrumental temperature records with more than 40 years of data, and then compared the results with those claimed by Berkeley Earth. These results were summarized in my last post.

The overall picture, based on the actual raw data, was that most states had experienced significant warming since 1980 but that the current temperatures were generally the same as those seen in 1880 or earlier. In most cases, the temperature records exhibited large swings in temperature between 1890 and 2000, typically a large decline in temperature up to 1950 and then a recovery; only Queensland exhibited a temperature trend that was anything like that advanced by the IPCC in their global instrumental temperature record, but Queensland has no data before 1887. And only in the case of Queensland did the temperature construction using the raw data qualitatively agree with the equivalent Berkeley Earth version. In the case of all other states the two sets of data (i.e. the one based on raw anomalies and the Berkeley Earth adjusted anomaly version) diverged significantly the further back in time before 1950 that you look, and generally the divergence was even greater in the 19th century.

What also became abundantly clear was that due to the large fluctuations seen over time intervals of more than 50 years, only temperature records that are at least 150 years in length allow the observer to put those fluctuations into their true context and to draw any meaningful conclusions. The temperature record is not as most climate scientists and the IPCC appear to claim: namely stable and constant before 1900 and exponentially rising thereafter. What has become clear to me is that the data is largely random but on multiple timescales. There are short-term fluctuations in the monthly means of up to ±5 °C, and long-term fluctuations on timescales of many decades or centuries that are often in excess of ±0.5 °C. In previous posts (see Post 9 and Post 17 in particular) I have speculated on the nature of these fluctuations, their scaling properties and whether they are fractal in nature.

In this post I will complete the analysis for Australia by using the regional temperature trends for each state to construct an average for the whole of Australia. The method will be straightforward: to weight each state's overall trend by the area of that state relative to that of the total area of Australia. Based on this methodology the weightings for each state are as follows:

NSW Victoria Tasmania South Australia Western Australia Northern Territory Queensland

0.1004 0.0284 0.0085 0.1229 0.3306 0.1776 0.2316

In addition, the trend from each state is renormalized with a fixed temperature offset in order to ensure that the mean anomaly of each state for the period 1961-1990 is zero. After the scaling by weighting and the renormalization, the contributions from each state are added. The resulting trend in the monthly mean temperature for the whole of Australia is shown below in Fig. 26.1 together with the 5-year moving average. As a result of the offsetting process, the temperature changes in Fig. 26.1 are all defined relative to the 1961-1990 average.

Fig. 26.1: The temperature trend for Australia since 1853. The best fit is applied to the interval 1871-2010 and has a gradient of 0.24 ± 0.04 °C per century. The temperature changes are relative to the 1961-1990 average.

The data in Fig. 26.1 shows that the five year average of the regional temperature for Australia, relative to the average for 1961-1990, decreased from a peak of +0.37 °C in 1879 to a minimum of -0.46 °C in 1909. It then recovered from a low of -0.38 °C in 1948 to reach another peak of +0.47 °C in 2007. So while it is true that temperatures rose by 0.85 °C from 1948 to 2007, it is also true that there was an almost equal but opposite fall of -0.75 °C during the 70 years prior to 1948. So, when put into context, the temperature rise since 1948 does not appear that cataclysmic. Yet when you look at the Berkeley Earth adjusted data for the same period, the picture is very different.

Fig. 26.2: The temperature trend for Australia since 1853 based on Berkeley Earth adjusted temperature data. The best fit is applied to the interval 1951-2008 and has a gradient of 1.51 ± 0.06 °C per century. The temperature changes are relative to the 1961-1990 average.

Fig. 26.2 shows the result of the same averaging process for the temperature anomalies in Australia as previously outlined for the data in Fig. 26.1. The only difference is that Fig. 26.2 uses Berkeley Earth adjusted anomaly data, and Fig. 26.1 uses the original data with the correct anomalies calculated for each station. Yet the two datasets look completely different. Whereas the raw data in Fig. 26.1 combines to form a U-shaped curve or parabola, the adjusted data forms a highly asymmetric curve, with little or no change in temperature before 1950 and a steep rise afterwards. That rise has a gradient of 1.51 ± 0.06 °C per century, which equates to a total rise from 1951 to 2008 of 0.88 °C. This is similar to that seen in Fig. 26.1 for the same time period, but without the preceding decline in temperature. However, while the adjusted data in Fig. 26.2 differs significantly from the raw data in Fig. 26.1, it agrees quite well with the trend published by Berkeley Earth and shown below in Fig. 26.3.

Fig. 26.3: The temperature trend for Australia since 1840 according to the Berkeley Earth website.

I believe that the level of agreement between the 12-month and 10-year moving average curves in Fig. 26.3 with those in Fig. 26.2 validates my approach, and therefore also validates the data in Fig. 26.1. The other point to note about the data in Fig. 26.1 is the gradient of the best fit line. This is 0.24 ± 0.04 °C per century and therefore equates to a total temperature rise of about 0.34 °C from 1871 to 2010. This is far more than the actual change of about 0.10 °C and illustrates the caution that needs to be applied to linear trends that are applied to non-linear data. 

Fig. 26.4: A comparison of the actual ten year average temperature trend for Australia since 1853 and the Berkeley Earth adjusted temperature version. The best fit is applied to the actual raw data over the interval 1859-2008 and has a gradient of 0.184 ± 0.056 °C per century. The temperature changes are defined relative to the 1991-2000 average.

If we contrast the raw data in Fig. 26.1 with the adjusted data in Fig. 26.2 by comparing the 10-year moving average of each (see Fig. 26.4 above) we see that after 1980 there is relatively close agreement between the two. However, as we go back in time before 1980, we see the curves diverge. If we compare the temperature change from 1880 to 2008 in each case, we see that the raw data shows evidence of a rise of only about 0.2 °C, while for the adjusted data the rise is over 0.6 °C. This difference is principally due to adjustments made by Berkeley Earth to the data. These adjustments are shown below in Fig. 26.5.

Fig. 26.5: The contribution of Berkeley Earth adjustments to the anomaly data after smoothing with a 12-month moving average. The linear best fit to the data is for the period 1901-2010 (red line) and the gradient is +0.295 ± 0.016 °C per century. The orange curve represents the contribution made to the blue adjustment curve by breakpoint adjustments only.

The total adjustments in Fig. 26.5 (blue curve) were determined by subtracting the raw monthly data in Fig. 26.1 from the equivalent curve for the sum of the adjusted data. The data was then smoothed with a 12-month moving average which removed over 90% of the noise. The breakpoint adjustment curve in Fig. 26.5 (the orange curve) is just the weighted sum of the breakpoint adjustment curves from the different states (see Posts 18-24). The breakpoints adjustments are determined from the Berkeley Earth station data by subtracting the Berkeley Earth raw anomaly (which is different from my raw anomaly because it uses homogenization) from the Berkeley Earth adjusted anomaly.

The curves in Fig. 26.5 above indicate that summing the Berkeley Earth adjustments to the anomaly data results in a curve that has a trend of gradient +0.295 ± 0.016 °C per century for the period 1901-2010. This in turn amounts to a contribution of over 0.4 °C between 1870 and 2010 as the same trend appears to extend back until at least 1870.

Concluding points

1) According to the raw data (shown in Fig. 26.1), temperatures in Australia may have risen by up to 0.8 °C over the last 60 years, but if so, they are still, at worst, no more than about 0.2 °C above some of the peak values seen in previous centuries. In all likelihood, the temperature rise is probably even less (the data in Fig. 26.1 suggests it may be less than 0.1 °C). Unfortunately a lack of data prior to 1853 precludes any more definitive conclusions than this.

2) The large changes in mean temperature seen over time in the instrumental temperature record for Australia appear to be natural and reversible, and therefore probably occur on a regular basis.

3) The adjustments made to individual temperature records through a combination of breakpoints and homogenization by Berkeley Earth do not appear to completely cancel when multiple station records are averaged. The analysis above suggests that such adjustments could actually add more than 0.4 °C to the warming trend for Australia, which would be more than double the amount that could be attributed to the raw data, as noted in Point 1 above.

25. A summary of temperature trends in Australia

In the seven posts previous to this I analysed the temperature trends in each of the seven major Australian states (ACT was combined with NSW) since instrumental temperature records began in about 1840. The results are summarized below.

In the following graphs the blue curve is the 10-year average temperature for the state relative to the decade 1991-2000 based on the actual unadjusted raw temperature data. The red line is the best fit to that data for the 100 year interval 1901-2000. The orange curve is the trend based on Berkeley Earth adjusted data. This is also defined relative to its mean for the decade 1991-2000.

Fig. 25.1: Temperature trends for NSW. The gradient of the best fit line is 0.08 ± 0.11 °C per century.

Fig. 25.2: Temperature trends for Victoria. The gradient of the best fit line is -0.04 ± 0.09 °C per century.

Fig. 25.3: Temperature trends for Tasmania. The gradient of the best fit line is 0.72 ± 0.11 °C per century.

Fig. 25.4: Temperature trends for South Australia. The gradient of the best fit line is 0.40 ± 0.11 °C per century.

Fig. 25.5: Temperature trends for Western Australia. The gradient of the best fit line is 0.76 ± 0.11 °C per century.

Fig. 25.6: Temperature trends for Northern Territory. The gradient of the best fit line is 0.09 ± 0.09 °C per century.

Fig. 25.7: Temperature trends for Queensland. The gradient of the best fit line is 0.69 ± 0.13 °C per century.

Conclusions

1) The Berkeley Earth adjusted data trends appear to closely follow the actual data trends for the period after 1970. However, before 1970 the two trends often diverge significantly.

2) Even after divergence, the Berkeley Earth adjusted data trend has almost identical features to the corresponding actual data trend. These features include the patterns of peaks, and the large changes in gradient at similar points in time. In fact the adjusted and unadjusted trend lines appear to show near identical instances of abrupt discontinuities and rapid temperature changes at various points along their respective records.

3) Linear regression fits to temperature record data cannot adequately represent the complexity of the data. For example, a 100-year best fit to the NSW data in Fig. 25.1 yields a gradient of 0.08 °C per century for the period 1901-2000, yet for the interval 1881-1980 this changes to -0.41 ± 0.11 °C per century. Likewise, changing the interval of the best fit for Northern Territory to 1886-1985 also changes the gradient to -0.41 ± 0.11 °C per century, while a best fit interval of 1871-1970 for South Australia results in a gradient of -0.60 ± 0.12 °C per century. In other words, the gradient of the best fit line depends strongly on the measurement interval chosen for the best fit.

4) The temperature trends based on actual data (not the Berkeley Earth adjusted data) suggest that for most states, except maybe Queensland, average temperatures in the latter part of the 20th century were lower than those in the latter part of the 19th century.

5) In most states the majority of any climatic warming has occurred after 1980.

Links to all posts with my original analysis are listed below or on the sidebar.

New South Wales (and ACT)

Victoria

Tasmania

South Australia

Western Australia

Northern Territory

Queensland

24. Queensland - temperature trends 0.7°C WARMING

i) Weather station quality and distribution

Queensland is the second largest state by area in Australia, but only the third largest by population. Given that the provision of weather station records around the world appears to broadly correlate with a combination of population and GDP, one would therefore expect Queensland to have more temperature records than smaller states such as Tasmania, South Australia and Northern Territory, but less than states with larger populations such as Victoria and New South Wales (NSW). This is broadly the case, although not in the case of Victoria.

Queensland has 112 stations with over 480 months of data (medium stations), of which 28 are long stations with more than 1200 months of data. This is not as extensive as NSW but more than Victoria. However, while Victoria has fewer stations in total, those long stations that it does have tend to have longer records. The major deficiency of the Queensland temperature records is that none pre-date 1887.

Fig. 24.1: The locations of long stations (large squares) and medium stations (small diamonds) in Queensland. Those stations with a high warming trend since 1887 are marked in red.

If we look at the distribution of weather stations in Queensland (see Fig. 24.1 above) we see that it is fairly even. There is a higher concentration around Brisbane and the Coral Sea coast compared to inland, but the coverage is generally fairly good, if a little sparse around the border with South Australia.


ii) The Berkeley Earth (BE) mean temperature trend

As the stations in Queensland are fairly evenly distributed (see Fig. 24.1 above), it means weighting coefficients based on the local station density are not necessary when combing stations into a regional average. This can be seen when averaging all the Berkeley Earth adjusted anomalies for each month. The resulting overall trend that is produced using a simple averaging process for that data (and plotted in Fig. 24.2) is very similar to that claimed by Berkeley Earth using their weighted averaging process (see Fig. 24.3).

Fig. 24.2: Temperature trend for all long and medium stations in Queensland since 1887 derived using the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1951-2003 and has a gradient of +1.74 ± 0.14 °C per century.

The Berkeley Earth trend in Fig. 24.2 above is my reconstruction of the Berkeley Earth adjusted trend. It was derived simply by averaging the adjusted anomalies for all long and medium stations. These adjusted anomalies were found in the data files for each station on the Berkeley Earth site. An example for Brisbane Regional Office Roof (Berkeley Earth ID: 152224) is found here. The adjusted anomaly data is in the 8th column. The raw temperature data is in the 3rd column.

The temperature trend in Fig. 24.2 clearly exhibits a period of stability from 1880 up to 1950, followed by a much stronger warming phase. This is replicated in the official Berkeley Earth version shown in Fig. 24.3 below, the original online version of which can be found here.

It is apparent that most of the prominent features (i.e. major peaks and troughs) displayed by both the 12-month moving average and the 10-year moving average for my reconstruction from the Berkeley Earth adjusted anomalies (shown in Fig. 24.2 above) correspond to similar features at almost identical times in the official Berkeley Earth trend shown below in Fig. 24.3. This implies that only a simple average of the data from Queensland is necessary in order to determine the overall trend for the region, and no station weighting (either based on their area of coverage or statistical significance) is needed.

Fig. 24.3: Temperature trend for Queensland since 1840 according to Berkeley Earth.

The degree of agreement between the data in Fig. 24.2 and Fig. 24.3 also suggests that the trend of the warming period in Fig. 24.2 above, which is approximately 1.74 ± 0.14 °C per century and denoted by the red line, will also correspond to the warming trend post-1920 in Fig. 24.3. This warming trend equates to a total warming since 1951 of about 1.0 °C. If we look at the raw temperature data though (rather than the Berkeley Earth adjusted data), we get a slightly different picture.


iii) Temperature trend based on long and medium station records

In this section I have applied the same simple averaging process to the raw temperature anomalies as was deployed in the last section for the Berkeley Earth adjusted anomalies. The raw anomalies for each dataset were derived by subtracting the monthly reference temperature (MRT) for that dataset from each monthly reading in that dataset. The 12 different MRTs were derived by averaging the temperature for each month in the dataset over the period 1961-1990. Then the mean anomaly for each month was determined by averaging all the values for that month from the different station datasets. The result is the regional monthly average shown in Fig. 24.4 below.

Fig. 24.4: Temperature trend for long and medium stations in Queensland since 1887. The best fit linear trend line (in red) is for the period 1901-2004 and has a gradient of 0.74 ± 0.08 °C per century.

The temperature trend in Fig. 24.4 is clearly positive over the entire time-frame, although the upward trend is more pronounced after 1950. This is different from the trend for all the other states in Australia, most of which exhibited a clear downward temperature trend before 1940. This difference may be due to the lack of data in Queensland before 1890, or it may be the result of regional variation. It should also be noted though that the trend for Queensland in Fig. 24.4 is very similar to that found for South Australia from 1900 onwards (see Fig. 21.5 here). Overall, the trend in Fig. 24.4 amounts to a total temperature rise since 1890 of 0.89 °C. This is slightly less than that seen for the Berkeley Earth adjusted data in Fig. 24.2.


iv) Breakpoints and other adjustments

Subtracting the mean temperature anomaly shown in Fig. 24.4 from the Berkeley Earth version derived using adjusted anomalies yields the data in Fig. 24.5 below.

Fig. 24.5: The difference between the raw anomaly data in Fig. 23.4 and Berkeley Earth adjusted anomaly data, together with a linear best fit for the period 1901-2010 (red line). The gradient of the best fit line is +0.02 ± 0.04 °C per century. The yellow curve represents the contribution made to the difference data by breakpoint adjustments.

The data in Fig. 24.5 appears to indicate that the Berkeley Earth adjustments are more or less neutral. This is not true, for while the overall contribution to the trend curve is minimal, there are within this two separate contributions which are not.

The first is for the period 1887-1950. Here the adjustments raise the temperatures before 1990, thereby flattening the curve. Then after 1951 the contribution is to increase the slope. The slope of the adjustments after 1951 is +0.15 ± 0.09 °C per century, while before 1951 it is -0.42 ± 0.09 °C.

Fig. 24.6: The contribution of Berkeley Earth adjustments to the anomaly data after smoothing with a 12-month moving average. The linear best fit to the data is for the period 1901-2010 (red line) and the gradient is +0.02 ± 0.04 °C per century. The orange curve represents the contribution made to the adjustment curve by breakpoint adjustments only.

The significant feature of the total adjustment data in Fig. 24.5 (the blue curve with black markers) is the amount of noise it contains, amounting to fluctuations of up to ±0.5 °C. Remarkably, a 12-month moving average completely removes this noise. This implies that the fluctuations are not random, but are periodic, with a period of 12 months. The obvious source of these fluctuations is the difference in the MRT between the values I have derived in my calculation of the temperature anomaly, and the homogenized values used by Berkeley Earth that also rely on data from neighbouring station records.


v) Conclusions

1) Queensland is the only state in Australia that exhibits a significant warming trend.

2) It is also the only state with no evidence of warming before 1890. That is because it is the only state with no significant data before 1890 (other than ACT).

3) The total temperature rise since 1890 is less than 0.9 °C.

23. Northern Territory - temperature trends STABLE

i) Weather station quality and distribution

Northern Territory has the lowest population and lowest population density of any state in Australia. It also has the lowest number of long and medium weather stations (other than ACT). In total only 20 temperature records contain more than 480 months of data, and only three of these have more than 1200 months of data.

Fig. 23.1: The locations of long stations (large squares) and medium stations (small diamonds) in Northern Territory. Those stations with a high warming trend since 1851 are marked in red.

The three long records are for Alice Springs Airport, Tennant Creek Post Office and Darwin Post Office. Of these, Alice Springs is the longest, while only Tennant Creek displays a strong warming trend (0.86 °C per century according to Berkeley Earth). The trend for Alice Springs is a modest 0.23°C per century, while for Darwin it is negative (-0.55°C per century).

Despite being low in number, the stations in Northern Territory are fairly evenly distributed (see Fig. 23.1 above). This means that when the average of all the Berkeley Earth adjusted anomalies are calculated for each month, the resulting overall trend that is produced using my simple averaging process for that data (and plotted in Fig. 23.2) is very similar to that claimed by Berkeley Earth using their weighted averaging process (see Fig. 23.3).


ii) The Berkeley Earth (BE) mean temperature trend

Fig. 23.2: Temperature trend for all long and medium stations in Northern Territory since 1879 derived using the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1921-2003 and has a gradient of +1.17 ± 0.06 °C/century.

The Berkeley Earth trends in Fig. 23.3 below clearly exhibit a slight cooling from 1880 up to 1920, followed by a much stronger warming. This is replicated in my reconstruction of those trends based on a simple average of the Berkeley Earth adjusted anomalies, as shown in Fig. 23.2 above.

It is apparent that most of the prominent features (i.e. major peaks and troughs) displayed by both the 12-month moving average and the 10-year moving average for my reconstruction from the Berkeley Earth adjusted anomalies correspond to similar features at almost identical times in the official Berkeley Earth trend shown below in Fig. 23.3 and published online here. This implies that only a simple average of the data from Northern Territory is necessary in order to determine the overall trend for the region, and no station weighting (either based on their area of coverage or statistical significance) is needed.

This also suggests that the trend of the warming period in Fig. 23.2 above, which is approximately 1.17 ± 0.06 °C per century and denoted by the red line, will also correspond to the warming trend post-1920 in Fig. 23.3 below. This warming trend equates to a total warming since 1920 of about 0.97 °C.

Fig. 23.3: Temperature trend for Northern Territory since 1840 according to Berkeley Earth.

There is, though, one slight problem with the above analysis: it doesn't correspond to reality. By reality I mean what the actual, original, raw data would indicate. For if we repeat the above analytical procedure, but use the original raw data instead of the Berkeley Earth adjusted data, then the picture is entirely different.


iii) Temperature trend based on long and medium station records

To do this we first must calculate the anomaly for each month of each temperature record using the monthly mean from 1961-1990 using only the data from that record. These 12 monthly mean values are what I term the monthly reference temperatures (MRTs) and the procedure used to determine them I described earlier in Post 5. This process does not use the homogenization that appears to occur in the Berkeley Earth process. In a future post I will show evidence of this automated homogenization, specifically in relation to some data I found from Zimbabwe that has been incorrectly attributed, and which thereby highlights the rationale at the heart of the Berkeley Earth process.

Next, the anomalies for each month are calculated by subtracting the MRTs from the raw data. Then the monthly anomalies from different records averaged. The result is shown in Fig. 23.4 below.

Fig. 23.4: Temperature trend for long and medium stations in Northern Territory since 1879. The best fit linear trend line (in red) is for the period 1882-2007 and has a gradient of -0.13 ± 0.07 °C/century.

The data in Fig. 23.4 is pretty unambiguous. It shows that there has been no warming of the climate in Northern Territory over the last 140 years. In fact the mean temperature has declined by about 0.2 °C over that time. The principal reason for the discrepancy between this data and the Berkeley Earth adjusted data is down to the adjustments made by Berkeley Earth. These are due to our old friends homogenization and breakpoints (see Fig. 23.5 below).


iv) Breakpoints and other adjustments

Fig. 23.5: The difference between the raw anomaly data in Fig. 23.4 and Berkeley Earth adjusted anomaly data, together with a linear best fit for the period 1881-2010 (red line). The gradient of the best fit line is +0.62 ± 0.03 °C per century. The yellow curve represents the contribution made to the difference data by breakpoint adjustments.

The data in Fig. 23.5 highlights the impact of both homogenization and breakpoint adjustments. The data in Fig. 23.5 is derived by subtracting the mean temperature anomaly shown in Fig. 23.4 from the Berkeley Earth adjusted anomaly. The difference is the total adjustment made by Berkeley Earth to the data for each month.

It can be seen that in combination these adjustments could potentially add 0.62 °C per century to the overall temperature trend. Between 1881 and 2010 this amounts to a temperature rise of more than 0.8 °C. In other words, almost all the temperature rise reported by Berkeley Earth for Northern Territory data in Fig. 23.3 can be attributed (depending on your point of view on how the data should be analysed) to inputs made by Berkeley Earth through their adjustment processes.

If this all sounds a bit noncommittal and ambiguous on my part, it is because it highlights what is in my view the central crux of the whole global warming debate. This is that the data is not complete, definitive and unambiguous, and therefore that all forms of analysis of that data are subjective, even the ones I have outlined in this blog. That is why all possible interpretations and explanations for climate change phenomena need to be considered, not just the prevailing orthodoxy. The issue, therefore, is not that Berkeley Earth and other climate scientists are definitely wrong, but that they might be.


v) Conclusions

1) According to the raw data, there has been no warming of the climate in Northern Territory since 1880.

2) The mean temperature in Northern Territory has declined by about 0.18 °C since 1880.

3) Adjustment processes used by climate scientists to process and average the temperature data could be responsible for virtually all of the temperature rise they claim has occurred in Northern Territory since 1900.

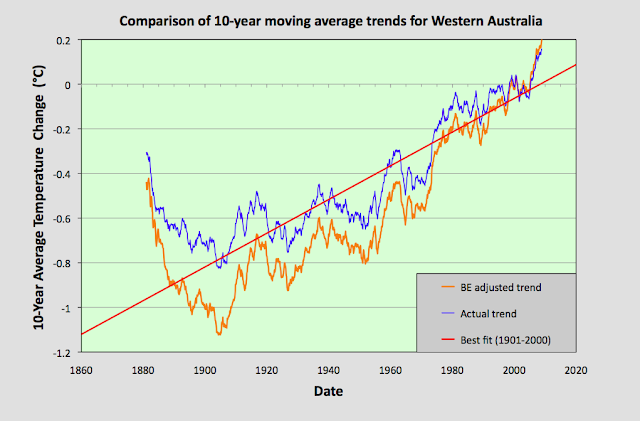
22. Western Australia - temperature trends 1°C WARMING

Western Australia is the first of the tropical states in Australia that I am going to examine. The Tropic of Capricorn (latitude 23.44° S) cuts through the state, separating the upper third from the rest. However, this does not appear to have any significant impact on the overall temperature trend which is similar to the that of other Australian states I have examined so far.


i) Weather station quality and distribution

Western Australia has the largest area of any Australian state (2.646 million km²), and the second lowest population density after Northern Territory. Despite its relatively low population, it still has 24 long stations with more than 1200 months of temperature data up to 2013, and 37 station records with more than 1000 months of data. In total, there are close to 100 long and medium stations with more than 480 months of data (see here).

Unfortunately, there is virtually no data prior to 1880. Only one station has data that precedes 1880 and that is Perth Regional Office (Berkeley Earth ID - 4321). This has some data that dates from 1852 (see Fig. 22.1 below), but only 40 months of it are before 1876 (see Fig. 22.1 below). The implication of this lack of early data will be discussed later in the post, but it certainly impacts on the interpretation of the overall trend. However, the trend for Perth Regional Office clearly exhibits the same features that we have seen for the regional anomalies in Victoria, South Australia and New South Wales. There is a minimum in the data around 1940 followed by a rise in temperature of about 1 °C. This rise is still less than the rise going back in time for the period from 1940 to 1880, thereby indicating that temperatures in the 1880s were probably higher than the present.

Fig. 22.1: The temperature anomaly for Perth Regional Office according to Berkeley Earth.

If we look at the distribution of weather stations in Western Australia we see that it is more uniform than was the case for South Australia and Tasmania, but not as uniform as was seen in Victoria and New South Wales. The greatest deficiency is the lack of station data for the interior of the state close to the borders with South Australia and Northern Territory. There are only 5 inland stations east of longitude 122E that are required to represent an area of over one million square kilometres. In addition, half the long stations are clustered in the south-west corner around Perth and Albany.

Fig. 22.2: The locations of long stations (large squares) and medium stations (small diamonds) in Western Australia. Those stations with a high warming trend since 1851 are marked in red.

ii) Temperature trend based on long and medium station records

If we average the long and medium station temperature anomalies for Western Australia we get the trend curve shown below in Fig. 22.3. These anomalies were calculated relative to their monthly reference temperatures (MRTs). In turn the MRTs were calculated from the 1961-1990 monthly average for each of the 12 months. 

Th trend curve in Fig. 22.3 is almost identical to that determined for South Australia (see Fig. 21.2). This similarity is easier to recognise if we consider the 5-year moving average (yellow curve). Common features include the peaks at 1910, 1920 and 1935, and the multiple peaks at 1960. In addition, both trends show similar magnitudes for the temperature rise from 1950 to 2010, and a similar fall from 1875 to 1910.

The most significant difference between the two trends is that the South Australia trend is longer. It extends back to 1857, and as a result it reveals the extent to which temperatures over that period were greater than they are today. This is not as evident if we look only at the Western Australia data in isolation. However, it is clear that the Western Australia data fits into the same consistent pattern that we have seen in South Australia, Victoria and New South Wales, and possibly Tasmania as well.

Fig. 22.3: Temperature trend for long and medium stations in Western Australia since 1876. The best fit linear trend line (in red) is for the period 1951-2010 and has a gradient of +1.19 ± 0.17 °C/century.

If we look at the temperature rise post-1950 in isolation we see that it amounts to 1.19 ± 0.17 °C per century (see red curve in Fig. 22.3). This amounts to a total temperature rise from 1951-2010 of about 0.7 °C. But as we know, this is only half the story, because it fails to account for the earlier temperature decline.

An additional feature of the data in Fig. 22.3 is the behaviour of the noise level. It appears to remain more or less constant in magnitude from 1880 up to 2010. Yet if we look at the number of stations in the average over this time-frame, this is not constant. Instead, it rises significantly from about 4 in 1880 to over 80 for the period 1960-2010.

Fig. 22.4: Number of stations per month included in the regional average for the Western Australia temperature anomaly.

Normally we would expect the noise to decrease with increased averaging, scaling as 1/√n where n is the number of terms in the average. In this case this should be manifested as a reduction in the noise level over more than a factor of 4. Yet none is seen. I have already speculated that this could be because of correlation effects between station data.


iii) The Berkeley Earth (BE) mean temperature trend

In all previous analyses we have seen that the Berkeley Earth temperature trend deviates significantly from that which one would expect based on the raw data. The data for Western Australia is no exception.

Fig. 22.5: Temperature trend for all long and medium stations in Western Australia since 1875 derived using the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1901-2010 and has a gradient of +1.02 ± 0.03 °C/century.

Summing the Berkeley Earth adjusted monthly averages yields a far longer and more consistent temperature rise over the course of the 20th century than is found for the raw data in Fig. 22.3. The gradient of this rise is +1.02 ± 0.03 °C and it results in a total temperature rise over the period 1901-2010 of more than 1.1 °C. This is 40% more than is seen the raw data. In addition, the peak in temperatures before 1900 is significantly reduced in size to only about 0.4 °C. The result is that Berkeley Earth graphs suggest that temperatures in 1880 were at least 0.7 °C below the present values (see Fig. 22.6 below), whereas the raw data suggests they were almost comparable.

Fig. 22.6: Temperature trend for Western Australia since 1840 according to Berkeley Earth.

The difference between the data in Fig. 22.5 and that in Fig. 22.3 is again primarily due to breakpoint adjustments. There are, however, noticeable differences between the data in Fig. 22.5 which I have reconstructed from the Berkeley Earth adjusted station data, and that shown in Fig. 22.6 which is the weighted average according to Berkeley Earth. While the trends are the same, and the 10-year moving average in each case have features that are generally coincident, there are bigger differences in the 12-month moving averages than were seen in the data for Victoria and New South Wales. This is probably due to the fact that the distribution of stations in Western Australia is less homogeneous than is the case for Victoria and New South Wales. However, it also shows that while the station distribution has affected the 12-month moving average, it has much less impact on data with longer smoothing intervals.


iv) Breakpoints and other adjustments 

Fig. 22.7: The difference between the data in Fig. 22.5 and Fig. 22.3 together with a linear best fit for the period 1902-2010 (red line). The gradient of the best fit line is +0.23 ± 0.03 °C per century. The yellow curve represents the total breakpoint adjustments.

Finally, if we look at the source of the difference between the results in Fig. 22.3 and 22.5, namely homogenization and breakpoint adjustments, we see that both appear to add to the warming trend between 1901 and 2010. The overall magnitude of this adjustment is about 0.25 °C, of which approximately 0.19 °C is due to the breakpoint adjustments.


iv) Conclusions

1) Temperatures in Western Australia before 1880 were probably similar to current temperatures. There is no evidence of significant anthropogenic climate change (see Fig. 22.3).

2) The temperature trend for Western Australia is consistent with that seen for all other states in Australia.

3) Temperatures in Western Australia were much lower in the 1940s than they are now (see Fig. 22.3).

4) The noise level in the regional average of monthly anomalies (see Fig. 22.3) is similar to the noise level in the individual records. Not only does the averaging process for the regional trend have little effect on the noise level, but the number of stations included in the average has little effect as well.

21. South Australia - temperature trends PARABOLIC

South Australia has a population density of 1.7 people per square kilometre. Only Western Australia and Northern Territory have lower densities. Yet South Australia still has 57 weather stations with more than 480 months of data. Of these 7 are long stations with more than 1200 months of data, and an additional 11 have between 900 and 1200 months of data. Its data is, therefore, comparable in terms of length and quality with that found in Victoria, but is still not as good as that for New South Wales.


i) Weather station distribution

The location of the 57 long and medium stations are shown in Fig. 21.1 below. Most of the stations are situated towards the south of the state, with only 10 medium stations located above the 32nd parallel (which bisects the state). This means that the stations in South Australia are not evenly distributed across the state, nor are they fully representative of the overall climate of the state.

Fig. 21.1: The locations of long stations (large squares) and medium stations (small diamonds) in South Australia. Those stations with a high warming trend since 1841 are marked in red.

The station locations shown in Fig. 21.1 differentiate between those stations that have warming trends and those where the trend is negative or stable. I have defined a warming trend to be one where the slope of the best fit to the temperature trend is positive and more than twice the error in the gradient (i.e. 95% confidence). Based on the distribution of stations in Fig. 21.1, it appears that most of the warming in South Australia is found in the west of the state. However, it needs to be recognized that most of those stations are shorter length stations with more recent data. As the data in Fig. 20.2 below indicates, the overall trend in South Australia is a warming one in the latter half of the 20th century. That coincides with the time-frame of operation of most of the medium and short stations.


ii) The trend in mean temperature

Fig. 21.2: Temperature trend for long stations in South Australia since 1857. The best fit linear trend line (in red) is for the period 1857-2012 and has a gradient of -0.087 ± 0.055 °C/century.

Adding the temperature anomalies from all stations in South Australia with more than 480 months of data yields the trend shown in Fig. 21.2 above. In this case the monthly reference temperatures (MRTs) for each station were calculated for the period 1961-1990. The MRT was then subtracted from the raw data to generate the temperature anomaly.

The trend in overall temperature since 1870 indicated in Fig. 21.2 is similar to that seen for both New South Wales and Victoria. There is evidence of a decline in temperatures from 1860 to 1940 followed by a slow rise. In this case the overall temperature trend from 1857 to 2012 (as indicated by the red line) is -0.087 ± 0.055 °C per century. In other words, overall South Australia has experienced a very low or moderate cooling since 1860. However, the real picture is of two distinct trends; a large cooling of over 1 °C for the period up to 1940, and a similar warming for the period since. This suggests that far from the climate being stable, it is continuously changing, and the warming we see in much of Australia since 1940 is not exceptional. Cooling phases of similar magnitudes have occurred previously.


iii) The Berkeley Earth (BE) mean temperature trend

Fig. 21.3: Temperature trend for long stations in South Australia since 1840 derived using the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1941-2010 and has a gradient of +1.66 ± 0.08 °C/century.

If we repeat the temperature averaging process for the Berkeley Earth adjusted data we get the trend shown above in Fig. 21.3. This also shows an initial slight downward trend before 1940, but one that only amounts to about 0.3 °C. After 1940 there is a strong positive trend of +1.62 ± 0.07 °C/century that raises the overall temperature by over 1.1 °C before 2010. The trend in Fig. 21.3 is qualitatively similar to the plot shown on the Berkeley Earth site (see Fig. 21.4 below), and also resembles both the IPCC "hockey stick" and the instrumental temperature record since 1850. Again, this level of agreement between the data in Fig. 21.3 and Fig. 21.4 effectively supports our averaging process as it implicitly refutes the need to introduce station weighting coefficients.

Fig. 21.4: Temperature trend for South Australia since 1840 according to Berkeley Earth.

The data presented in Fig. 21.3 and Fig. 21.4 is the 12-month moving average, but the same general trends in the data are also seen in the monthly averages of the Berkeley adjusted data (see Fig. 21.5 below). The best fit to this data over the period 1841-2010 is a modest 0.429 ± 0.052 °C per century, but this still equates to an overall temperature rise of more than 0.8 °C since 1841. That is indeed similar to the temperature rise seen after 1941 for the raw data in Fig. 21.2, but the overall picture it presents is completely different. The reason for the difference becomes apparent if you look at how and where the differences arise.

Fig. 21.5: Temperature trend for all long and medium stations in South Australia since 1857 based on Berkeley Earth adjusted monthly data. The best fit linear trend line (in red) is for the period 1857-2012 and has a gradient of +0.429 ± 0.052 °C/century.

iv) Comparison of unadjusted and BE adjusted temperature data

The difference between the data in Fig. 21.5 and that in Fig. 21.2 is almost entirely due to the adjustments made to the data by Berkeley Earth (BE). These adjustments are shown in Fig. 21.6 below.

The adjustments made to the data by Berkeley Earth appear to be of two main types. Generally, the most significant tend to be the breakpoint adjustments that I have discussed previously. These are supposed to compensate for measurement errors in the original data. However, there appears to be a second adjustment that is introduced when the MRTs are calculated. As I wrote previously, the source of this is unclear, but I suspect it arises from a homogenization process being used to determine the MRT for each dataset, rather than the MRT being determined purely by averaging the data from within that dataset as I have done for Fig. 21.2.

Fig. 21.6: The Berkeley Earth breakpoint adjustment (in yellow) for Tasmania since 1840 together with the difference between the Berkeley Earth adjusted anomaly and the raw anomaly (in blue). The best fit (red line) to the total adjustment (blue curve) is +0.30 ± 0.03 °C per century.

In the case of the South Australia data, the MRT adjustments, although large in amplitude, do not seem to have as great an impact on the trend as the breakpoint adjustments.  The sum total of the two adjustments is illustrated by the blue curve in Fig. 21.6 above. Together they add 0.30 ± 0.03 °C per century to the trend between 1911 and 2010 (see the red best fit line in Fig. 21.6). Of this, the breakpoint adjustments contribute 0.19 °C per century (see the yellow curve in Fig. 21.6). The net result is to lift the slope of the trend curve by 0.3 °C per century between 1911 and 2010. That amounts to a rise in the final temperature after 2010 of 0.3 °C as well. This, though, is only half the story.

What we can also see in Fig. 21.6 is that the total effect of all the adjustments is to introduce a negative cooling for the period 1857-1900 of up to 1 °C. The justification for this is presumably that the high temperatures before 1900 are inconsistent will the global trend. The problem is that they are all too consistent with the trends seen in the rest of Australia and in New Zealand.

As I pointed out in the last post, you do not need to eradicate the peaks and troughs in the temperature trend before 1900 (and nor should you) because these peaks and troughs are real, not erroneous artefacts that need to be expunged. And even if these peaks and troughs are not real, the appropriate way to deal with them is to use more data and see if they average out. In the case of Tasmania this was not possible because there was only one significant but imperfect temperature record for the period 1840-1900. In South Australia, however, we have at least four. And like the Tasmania data, it is consistent with data in NSW and Victoria over the same time-frame.

As I have outlined above, these adjustments that Berkeley Earth apply are not neutral. They significantly alter the temperature trend, and they do this because they do not just add to the positive trend post-1940 (thus enhancing the blade of the so-called hockey stick), they also help to erase the peaks in the anomaly data before 1990 (thereby smoothing the handle of the hockey stick). It is the combination and interaction of these two effects that so dramatically changes the temperature trend from the one I have calculated in Fig. 21.2 to the Berkeley Earth version in Fig. 21.5.



v) Noise and its scaling behaviour

Fig. 21.7: The standard deviation of the South Australia mean anomaly after smoothing with a moving average of size N. The gradient of the best fit line is -0.290 ± 0.015 and R² = 0.9869.

Finally, if we look at the effect of data smoothing on the noise level, we again appear to see strong evidence of scaling behaviour (see Fig. 21.7 above). Once again the noise (as defined by the standard deviation) scales as N ^-a with the exponent a = 0.290 ± 0.015. This is similar to the scaling seen previously for NSW (a = 0.272 ± 0.005) and Victoria (a = 0.257 ± 0.015). However, here things are not quite so straight-forward.

The data in Fig. 21.7 shows evidence of a distinct curvature away from the linear regression best fit line. This suggests that the scaling may only be valid for low values of N and the log-log plot may not be truly linear. This appears to be confirmed by the plot in Fig. 21.8 below.

Fig. 21.8: The standard deviation of the South Australia mean anomaly after smoothing with a moving average of size N , but with a negative offset of 0.2 applied each time. The gradient of the best fit line is -0.465 ± 0.007 and R² = 0.9988.

In Fig. 21.8 the standard deviation for each set of smoothed data is offset by a fixed amount (in this case 0.2). The reasoning here is that some of the standard deviation may not be from noise, but from an underlying linear trend for the data such as that seen in the upward slope of the Berkeley Earth data in Fig. 21.3 after 1940. Such a slope would itself have a standard deviation of ∆y/4√3 where ∆y is the change in vertical height up the slope.

The data in Fig. 21.2 effectively has two such slopes, a negative one before 1940 and a positive one after. Each slope will have the same standard deviation of 0.2 °C as ∆y = 1.4 °C (approximately) in each case. Thus if we subtract 0.2 from each standard deviation in Fig. 21.7 we get an approximate value for the standard deviation of the noise and not the slope. This data is plotted in Fig. 21.8 above.

What we find is that we still get a power law of the type N ^-a, but the index changes to a = 0.465 ± 0.007. More significantly, the residual between the data and the best fit reduces significantly from 11.4% of the standard deviation of y-values to 3.5%, thereby indicating how much the linear regression best fit has improved.

Fig. 21.9: The standard deviation of the South Australia mean anomaly, minus the parabolic best fit, after smoothing with a moving average of size N. The gradient of the best fit line is -0.465 ± 0.007 and R² = 0.9988.

Alteratively, we could remove the underlying trend in Fig. 21.2 altogether. This trend is clearly parabolic to first order and can be approximated by the equation y = a(x-b)² - c, where a = 0.00016, b = 1940, and c = 0.2. Subtracting this function from the mean anomaly data in Fig. 21.2 yields a dataset which has no underlying warming trend for the the entire timescale 1857-2013, but has the same monthly fluctuations as the data in Fig. 21.2. If the same scaling analysis is performed on this modified data as was undertaken in Fig. 21.7, the result is a different power law as shown in Fig. 21.9. This time we find that a = 0.456 ± 0.007. This is very close to the value of 0.5 we would expect for white noise. In addition the residual reduces even further to 3.4%.

So do we have white noise on a smoothly varying background (as demonstrated by Fig. 21.9) or do we have a quasi-fractal with a much lower power law? So far it is too early to tell. We do not have enough data. What is clear is that it is not only the South Australia data that exhibits this behaviour. It can also be seen (but was missed on first analysis) in Victoria (see Fig. 19.7) and Tasmania (see Fig. 20.8). In these two cases, however, the underlying trend was not parabolic or linear, particularly before 1900, so the modifications made in Fig. 21.8 and Fig. 21.9 above would not be applicable. In order to investigate this further, we probably need longer datasets. These will only be found in the Northern Hemisphere.


vi) Conclusions

1) The overall temperature trend for South Australia since 1857 shows no evidence of anthropogenic climate change.

2) Temperatures in the 1850s were probably greater than they are now.

3) Temperatures were much lower in the 1940s than they are now. 

4) The overall temperature trend for South Australia since 1860 is broadly similar to that seen for both New South Wales and Victoria.

5) Berkeley Earth breakpoint adjustments and other adjustments (possibly from homogenization) have once again significantly changed the form and shape of the long-term temperature trend (see Fig. 21.3 and Fig. 21.5 and Fig. 21.6).

6) The noise level in the regional average of monthly anomalies (see Fig. 21.3) is similar to the noise level in the individual records. The averaging process has little effect on the noise level.

7) The noise in the regional temperature average for South Australia may scale in a similar way to that seen for New South Wales except that the power law is N ^{- 0.29}, where N is the size of the sliding window in the moving average (see Fig. 21.7). Or it could be white noise on a parabolic (or sinusoidal) background signal (see Fig. 21.9).

20. Tasmania - temperature trends STABLE

i) Weather station distribution

Hobart (Ellerslie Road) is the station with the longest temperature record in Australia, dating back to 1841. Unfortunately this record is not continuous as can be seen in Fig. 20.1 below (taken from Berkeley Earth).

Fig. 20.1: Temperature anomaly for Hobart - Ellerslie Road (Berkeley Earth ID - 151745).

This is indicative of the overall state of weather station data in Tasmania. It is good, but not good enough. The state of Tasmania in Australia has only 28 sets of weather station data that are longer than 480 months (the equivalent of 40 years), of which only 2 are long stations with over 1200 months of data. Compared to Victoria and New South Wales these numbers are very low. Moreover, most of those stations are located on the north and east coasts, with only 10 situated inland (see Fig. 20.2 below). This means that the stations in Tasmania are not evenly distributed across the state, nor are they fully representative of the overall climate of the state.

Fig. 20.2: The locations of long stations (large squares) and medium stations (small diamonds) in Tasmania. Those stations with a high warming trend since 1841 are marked in red.

The station locations shown in Fig. 20.2 differentiate between those stations that have warming trends and those where the trend is negative or stable. I have defined a warming trend to be one where the slope of the best fit to the temperature trend is positive and more than twice the error in the gradient (i.e. 95% confidence). Based on the distribution of stations in Fig. 20.2, it appears that most of the warming in Tasmania is found in largest city, Hobart, and around the coast. Similar trends were seen in New South Wales and Victoria. It can be seen in Fig. 20.2 that only 5 of the 28 stations have a stable or cooling trend. However, as was the case in Victoria, it is the shorter length stations with more recent data where the warming is more pronounced.


ii) The trend in mean temperature

Fig. 20.3: Temperature trend for long stations in Tasmania since 1840. The best fit linear trend line (in red) is for the period 1841-2010 and has a gradient of +0.135 ± 0.049 °C/century.

Adding the temperature anomalies from all stations in Tasmania with more than 480 months of data yields the trend shown in Fig. 20.3 above. In this case the monthly reference temperatures (MRTs) were calculated for the period 1961-1990 as this period enabled the greatest number of stations to be included in the average.

The trend in Fig. 20.3 similar to that for New South Wales shown in Fig. 18.3 previously. There is evidence of a decline in temperatures from 1880 to 1940 followed by a slow rise. In this case the overall temperature trend from 1890 to 2007 (as indicated by the red line) is +0.135 ± 0.049 °C per century. In other words, only a very low or moderate warming is taking place over the entire period. However, the trend for the period 1941-2010 is +1.29 ± 0.14 °C per century, which equates to a temperature rise of over 0.9 °C since 1941. This is more than balanced though by a large (but incomplete) peak in temperature before 1900.


iii) The Berkeley Earth (BE) mean temperature trend

Fig. 20.4: Temperature trend for long stations in Victoria since 1840 derived using the Berkeley Earth adjusted data. The best fit linear trend line (in red) is for the period 1941-2010 and has a gradient of +1.62 ± 0.07 °C/century.

If we repeat the temperature averaging process for the Berkeley Earth adjusted data we get the trend shown above in Fig. 20.4. This also shows an initial slight downward trend, but only before 1940, after which there is a strong positive trend of +1.62 ± 0.07 °C/century that raises the overall temperature by over 1.1 °C before 2010. The trend in Fig. 20.4 is almost identical to the plot shown on the Berkeley Earth site (see Fig. 20.5 below), and also resembles both the IPCC "hockey stick" and the instrumental temperature record since 1850, at least qualitatively.

Fig. 20.5: Temperature trend for Tasmania since 1840 according to Berkeley Earth.

The data in Fig. 20.4 and Fig. 20.5 is the 12-month moving average, but the same pattern of data is also seen in the monthly averages of the Berkeley adjusted data (see Fig. 20.6 below). The best fit to this data over the period 1841-2010 is a modest 0.496 ± 0.049 °C per century, but this still equates to an overall temperature rise of more than 0.84 °C since 1841.  That is similar to the temperature rise seen after 1941 in Fig. 20.3. The obvious question is which graph is correct: the one in Fig. 20.3 or the one in Fig. 20.6 below?

Fig. 20.6: Temperature trend for all long and medium stations in Tasmania since 1840 based on Berkeley Earth adjusted monthly data. The best fit linear trend line (in red) is for the period 1841-2010 and has a gradient of +0.496 ± 0.056 °C/century.

iv) Comparison of unadjusted and BE adjusted temperature data

The difference between the data in Fig. 20.6 and that in Fig. 20.3 is almost entirely due to the adjustments made to the data by Berkeley Earth (BE). These adjustments are shown in Fig. 20.7 below.

The adjustments made to the data by Berkeley Earth appear to be of two main types. The most significant are the breakpoint adjustments that I have discussed previously. These are supposed to compensate for measurement errors in the original data. However, there appears to be a second adjustment that is introduced when the MRT is calculated. As I wrote last time, the source of this is unclear, but I suspect it arises from a homogenization process being used to determine the MRT for each dataset, rather than the MRT being determined by just averaging the data from within that dataset as I have done for Fig. 20.3. In the case of the Tasmania data, the MRT adjustments, although large in amplitude, do not seem to have a great impact on the trend. It is the breakpoint adjustments that affect the trend, as illustrated in Fig. 20.7 below.

Fig. 20.7: The Berkeley Earth breakpoint adjustment (in yellow) for Tasmania since 1840 together with the difference between the Berkeley Earth adjusted anomaly and the raw anomaly (in blue). The best fit (red line) to the breakpoint adjustment data is +0.25 ± 0.12 °C per century.

What we can see in Fig. 20.7 is that the total effect of all the adjustments is to introduce a positive warming of +0.25 ± 0.12 °C/century for the period 1941-2010. This equates to a temperature rise of at least 0.18 °C being added to the original data between 1941 and 2010 by the Berkeley Earth data processing, but this is much less than the adjustments seen for the data from Victoria and NSW. These adjustments are not neutral, though, and they significantly alter the temperature trend. This is because they do not just add to the positive trend post-1941 (thus enhancing the blade of the hockey stick), they also help to erase the peaks in the anomaly data before 1990 (thereby smoothing the handle of the hockey stick). What we need to ascertain is whether these alterations are justified.

Normally, we would be extremely cautious about the data in Fig. 20.3 before 1900 as it has a number of significant deficiencies.

Firstly, it is based on only one temperature record, Hobart (Ellerslie Road). That means the statistical error will be high.

Secondly, it is not continuous. That means there is a high probability of there being defective data in this time interval.

Thirdly, the data after 1900 appears qualitatively different from that before 1900.

However, the data before 1900 has one major virtue. It is consistent with data in NSW and Victoria over the same time-frame. Both NSW and Victoria exhibit peaks in their temperature records at 1880, that then decline significantly as you go back further in time to 1860. That is the evidence that corroborates the Tasmania data. It is also the evidence that negates the need for the breakpoint adjustments. You do not need to eradicate the peaks and troughs in the temperature trend before 1900 because these peaks and troughs are real, not erroneous artefacts that need to be expunged.

One final point to note is how the data in Fig. 20.3 compares well with similar data for Victoria and New South Wales despite the distribution of weather stations in Tasmania being less than ideal. This again suggests that, while the distribution may be sub-optimal and may not reflect the whole of Tasmania geographically, there resulting temperature trend may be much more representative.


v) Noise and its scaling behaviour

Fig. 20.8: The change in standard deviation of the Tasmania mean anomaly after smoothing with a moving average of size N. The gradient of the best fit line is -0.217 ± 0.007 and R² = 0.9946.

Finally, if we look at the effect of data smoothing on the noise level, we again see strong evidence of scaling behaviour (see Fig. 20.8 above). Once again the noise (as defined by the standard deviation) scales as N ^-a with the exponent a = 0.217 ± 0.007. Again, this is similar to the scaling seen previously for NSW (a = 0.272 ± 0.005) and Victoria (a = 0.257 ± 0.015). It indicates that when smoothed with a 5-year moving average the data will still have a standard deviation of 0.38 °C. This implies that there is a 50% probability of fluctuations in the 5-year moving temperature average exceeding 0.7 °C over any 100 year interval. In addition the standard deviation for a 100-year moving average, determined by interpolation, will be 0.19 °C, again suggesting that the long-term fluctuations in temperature will be significant.


vi) Conclusions

1) Based on the original station data, there is no evidence of any rise in overall temperatures in Tasmania since 1841 (see Fig. 20.3).

2) The overall temperature trend for Tasmania since 1850 is broadly similar to that seen for both New South Wales and Victoria.

3) The long-term temperature trend for Tasmania exhibits fluctuations of more than ±2 °C over timescales of more than 100 years (see Fig. 20.3). Even the 5-year moving average has fluctuations of at least ±0.5 °C, and maybe as much as ±1 °C. This adds to previous evidence that suggests that what we are probably seeing in these temperature trends is primarily low frequency noise or random fluctuations.

4) Breakpoint adjustments and other adjustments (possibly from homogenization) can completely change the form and shape of the long-term temperature trend (see Fig. 20.4). They are not neutral.

5) Breakpoint adjustments added at least 0.25 °C to the long-term temperature trend for Tasmania since 1941 (see Fig. 20.7).

6) The noise in the regional temperature average for Tasmania scales in a similar way to that seen for New South Wales and Victoria except that the power law is N ^-0.22, where N is the size of the sliding window in the moving average (see Fig. 20.8).

7) As the standard deviation for the 60-month smoothed temperature anomalies is 0.38 °C, this means that there is still a 50% probability of a temperature rise of more than 0.70 °C occurring over the course of a century in Tasmania purely by random chance, as I explained here.

8) The statistical results presented here, and for New South Wales and Victoria previously, imply that chaotic effects in the temperature record are important, and probably dominant in many cases, even over long (i.e. more than 100 years) timescales.