52. Texas - temperature trends STABLE

If there is one country in the world where you expect dramatic climate change on account of its own greenhouse gas emissions, then that country would probably be the USA. And if there is one state in the USA that embodies the American passion for fossil fuels, that state would be Texas. So when Texas was hit by extreme weather earlier this month in the shape of winter storms Uri and Viola, which resulted in millions Texans losing their electricity supply, then it was only a matter of time before people started screaming "climate change". Because even extreme cold weather is a symptom of anthropogenic global warming (AGW) and climate change (apparently). Unfortunately there is just one problem: there has been no global warming in Texas. So, given the topical nature of the Texas climate at the moment, I thought I would take a temporary break from Europe and take a closer look at climate change in Texas.

The mean temperature trend for the region is shown in Fig. 52.1 below. This was achieved by averaging the temperature anomalies from the 220 longest weather station temperature records in the region, where the temperature anomalies were measured relative to the monthly reference temperature (MRT) in each case. The MRTs were calculated for the interval 1961-1990. For a more detailed explanation of the MRT calculation process, see Post 47.

 

 Fig. 52.1: The temperature trend for Texas since 1840. The best fit is applied to all the data and has a slight positive gradient of 0.05 ± 0.08 °C per century. The monthly temperature changes are defined relative to the 1961-1990 monthly averages. 

 

For 160 years up to 2013 there was no anthropogenic global warming (AGW) occurring in Texas. In fact the mean temperature for the region rose by less than 0.08 °C. And while there is some evidence of a rise in temperature since the 1960s, this still leaves temperatures lower than in the first half of the 20th century.

 

Fig. 52.2: The number of station records included each month in the mean temperature trend for Texas.

 

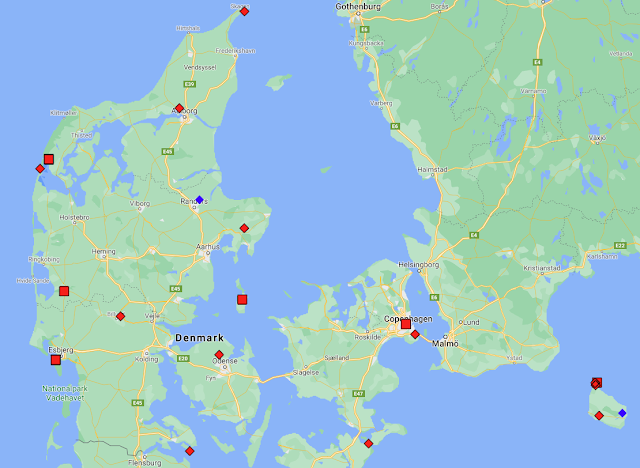
The temperature trend shown in Fig. 52.1 is the average of up to 220 of the longest temperature records for the state as illustrated in Fig. 52.2 above. All the temperature records have over 720 months (or 60 years) of data, of which 64 are long stations with more than 1200 months of data. These 220 stations are also distributed fairly evenly over the region as shown in Fig. 52.3 below. This means that a simple average of all the temperature anomalies without additional weighting coefficients should yield a mean temperature trend that is reasonably accurate, even though there does appear to be a slightly higher density of stations in the east of the state than in the west. This conjecture will be tested by comparing results later.

 

Fig. 52.3: The locations of long stations (large squares) and medium stations (small diamonds) in Texas. Those stations with a high warming trend are marked in red.

 

The other point of note about the stations in Fig. 52.3 is the high proportion of stations that appear to exhibit no warming; over 70% of them. Here, a warming station is defined as being one where the temperature gradient is more than twice the uncertainty in the trend and the total temperature rise also exceeds 0.25 °C. 

This high proportion of cool stations is unusual but not unique. It has seen in many other places including New South Wales and Victoria. What it appears to highlight is the strong correlation that exists between the degree of warming seen at a particular location and the size of the local population, degree of economic development and the length of the temperature record itself. 

Short, younger temperature records tend to exhibit greater warming because they only have data from the latter part of the 20th century and post 2000, and increased urbanization in the latter part of the 20th century is clearly warming the local environment. In fact, direct anthropogenic surface heating (DASH) or waste heat equating to about 0.7 W/m² has probably warmed Texas by up to 0.3 °C since 1850. In addition, the short length of modern station records means that they do not include any of the natural variation seen in earlier times such as naturally high temperatures seen in the 19th century. In addition, many rural stations appear to exhibit very little warming, while major cities like Jakarta, Sydney and Melbourne can display very large degrees of warming that do not correspond to the climate of the rest of their regions.

What is interesting is comparing the trend based on the original true temperature data in Fig. 52.1 with the equivalent trend based on an average of the adjusted data used by Berkeley Earth. This adjusted data includes the effects of homogenization and breakpoint adjustments that are supposed to improve the quality and accuracy of the data. The mean of the adjusted Berkeley Earth data for the 220 longest station records in Texas is shown in Fig. 52.4 below.

 

Fig. 52.4: Temperature trend in Texas since 1840 derived by aggregating and averaging the Berkeley Earth adjusted data for the 220 longest data records for Texas. The best fit linear trend line (in red) is for the period 1881-2010 and has a gradient of +0.58 ± 0.04 °C/century.

 

Unlike the original data in Fig. 52.1 which exhibits virtually no warming, the Berkeley Earth adjusted data has a strong positive trend of 0.58 °C per century. In total this equates to a warming of over 0.8 °C from 1880 to 2010, while the 10-year moving average suggests an even greater warming of over 1.2 °C. Again, this may be consistent with IPCC reports, but it is not consistent with the actual real data in Fig. 52.1. It is, however, virtually identical to the published Berkeley Earth version shown in Fig. 52.5 below.

 

 Fig. 52.5: The temperature trend for Texas since 1820 according to Berkeley Earth.

 

The similarity of the data in Fig. 52.4 with the Berkeley Earth published version shown in Fig. 52.5 above in effect validates the simple averaging process I have employed, not only for the data in Fig. 52.4, but also for that in Fig. 52.1 as well. It demonstrates that weighted averages are not needed.

Fig. 52.6: The contribution of Berkeley Earth (BE) adjustments to the anomaly data in Fig. 52.4 after smoothing with a 12-month moving average. The blue curve represents the total BE adjustments including those from homogenization. The linear best fit (red line) to these adjustments for the period 1911-2010 has a gradient of +0.568 ± 0.003 °C per century. The orange curve shows the contribution from breakpoint adjustments only.

 

Overall, the Berkeley Earth adjustments appear to add between 0.6 °C and 1.2 °C to the warming of Texas, depending on how you view it. If we consider the net adjustments made to the data (the blue curve in Fig. 52.6 above) which are the difference between the mean anomalies in Fig. 52.1 and Fig. 52.4, these appear to add about 0.6 °C of warming. On the other hand, the difference in the gradients of the best fit lines in Fig. 52.1 and Fig. 52.4 results in over 0.7 °C of warming being added. Either way, these are significant modifications to the original real data that completely change its properties.

 

Summary

1) The mean temperature of Texas has been stable since 1840 (see Fig. 52.1).

2) In contrast, the Texas temperature trend based on Berkeley Earth adjusted data exhibits a warming of over 0.8 °C before 2010 (see Fig. 52.4).

3) Virtually all the warming seen in the Berkeley Earth adjusted data (as denoted by the trend of 0.58 °C per century in Fig. 52.4) can be accounted for by the adjustments made to the data (as seen in the trend of 0.57 °C per century in Fig. 52.6).

4) Adjustments made to the temperature data by Berkeley Earth via breakpoint adjustments and homogenization (see Fig. 52.6) have profoundly changed the magnitude of the warming of the Texas temperature trend since 1840 (see Fig. 52.4) compared with that observed in the raw original data (see Fig. 52.1).

 

51. The Baltic States - temperature trends STABLE to 1980

The Baltic States are the countries of Lithuania, Latvia and Estonia that used to be part of the USSR and are now part of the EU. For the purpose of geographical convenience I will also include the enclave of Kaliningrad in this analysis, for while it is actually a part of Russia, it is not contiguous with Russia, but is instead bordered by Poland, Lithuania and the Baltic Sea.

The mean temperature trend for the region is shown in Fig. 51.1 below. This was achieved by averaging the temperature anomalies for all the weather station temperature records in the region, where the temperature anomalies were measured relative to the monthly reference temperature (MRT) in each case. The MRTs were calculated for the interval 1991-2010. This is rather later and shorter (only 20 years rather than 30) than usual due to the need to maximize the available data and avoid the jump in temperature in 1988. For a more detailed explanation of the MRT calculation process, see Post 47.

 

Fig. 51.1: The temperature trend for the Baltic States since 1775. The best fit is applied to the interval 1781-1980 and has a negative gradient of -0.08 ± 0.08 °C per century. The monthly temperature changes are defined relative to the 1991-2010 monthly averages.

 

For 200 years up to 1980 there was no anthropogenic global warming (AGW) occurring in the Baltic States. In fact the mean temperature for the region fell by about 0.15 °C. Then around 1988 it suddenly jumped by about 1.1 C (see Fig. 51.1 above). Even then the temperature is less than it was in the 1820s, although the data for that period needs to be treated with some caution. That is because it is based on less than five station temperature records (see Fig. 51.2 below). 

However, the more significant factor in explaining the caution over the temperature peak around 1824 in Fig. 51.1 is probably the fragmentation of some of the temperature records in that era, particularly for Dorpat, Tallinn and Riga. This, when combined with the low number of stations overall, can lead to discontinuities in the temperature trend. 

Having said that, data from Vilnius, Sovetsk and Mitau all appear to show similar peaks in the temperature trend around 1824, and their data are continuous. So maybe the peak around 1824 is real. In which case temperatures in the 1820s really were higher than today.

Fig. 51.2: The number of station records included each month in the mean temperature trend for the Baltic States when the MRT interval is 1991-2010.

The temperature trend shown in Fig. 51.1 is the average of just 23 medium and long station records with over 480 months of data. Of these, seven are long stations with more than 1200 months of data. In fact four have over 1800 months (or 150 years) of data. The 23 stations are also distributed evenly over the region as shown in Fig. 51.3 below, with each of the four regions (Kaliningrad, Lithuania, Latvia and Estonia) also containing one of the four longest records. The HTML links above link to a list of stations for each region.

Fig. 51.3: The locations of long stations (large squares) and medium stations (small diamonds) in the Baltic States. Those stations with a high warming trend are marked in red.

What is interesting is comparing the trend based on the original true temperature data in Fig. 51.1 with the equivalent trend based on the data used by Berkeley Earth after they have adjusted the data. The Berkeley Earth version is shown in Fig. 51.4 below.

Fig. 51.4: Temperature trend in the Baltic States since 1775 derived by aggregating and averaging the Berkeley Earth adjusted data for all long and medium stations. The best fit linear trend line (in red) is for the period 1841-2010 and has a gradient of +0.45 ± 0.04 °C/century.

Unlike the original data which has a slight negative trend before 1980, the Berkeley Earth adjusted data has a strong positive trend of 0.45 °C per century. In total this equates to a warming of over 0.8 °C before 1980. When the temperature jump after 1980 is included, the total temperature rise since 1800 is over 2 °C. This may be consistent with IPCC briefings, but it is not consistent with the actual real data in Fig. 51.1.

Fig. 51.5: The contribution of Berkeley Earth (BE) adjustments to the anomaly data in Fig. 51.4 after smoothing with a 12-month moving average. The blue curve represents the total BE adjustments including those from homogenization. The linear best fit (red line) to these adjustments for the period 1841-2010 has a gradient of +0.351 ± 0.007 °C per century. The orange curve shows the contribution from breakpoint adjustments.

Overall, the Berkeley Earth adjustments appear to add between 0.6 °C and 1.0 °C to the warming, depending on how you view it. If we consider the net adjustments made to the data (the blue curve in Fig. 51.5 above) which are the difference between the mean anomalies in Fig. 51.1 and Fig. 51.4, these appear to add about 0.6 °C of warming. The difference in the gradients, however, results in over 0.9 °C of warming being added. Either way, these are significant modifications to the real data that completely change its properties.

Summary

1) In the 200 years before 1980 the mean temperature of the region decreased by 0.15 °C (see Fig. 51.1).

2) Once again we see a sudden rise in temperature in 1988 of about 1 °C that is difficult to explain (see Fig. 51.1). Similar rises were seen in Poland (see Post 50), Germany (see Post 49) and Denmark (see Post 48).

3) Even after the 1988 temperature rise, temperatures post-2000 are still below those pre-1830 (see Fig. 51.1).

4) The temperature trend based on Berkeley Earth adjusted data has a warming of over 0.8 °C before 1980 and over 1 °C of additional warming after 1980 (see Fig. 51.4).

5) Adjustments made to the temperature data by Berkeley Earth via breakpoint adjustments and homogenization have profoundly changed both the magnitude of the warming since 1800 and its significance (see Fig. 51.4 and Fig. 51.5).

50. Poland - temperature trends WARMING 0.9°C

There are over 100 temperature records for Poland. The longest is the Warsaw record (Berkeley Earth ID: 157587) which dates back to 1779 (see Fig. 50.1 below) and exhibits a strong warming trend of 0.71 °C per century. However, this warming trend is not continuous but has considerable variability, with temperatures in the 1930s being comparable to those of today.

 

Fig. 50.1: The temperature trend for Warsaw since 1779. The best fit is applied to the interval 1811-2010 and has a positive gradient of +0.71 ± 0.08 °C per century. The monthly temperature changes are defined relative to the 1951-1980 monthly averages. 

 

Of the 100 or more stations in Poland (for a full list see here), 60 have over 480 months of data (these are medium stations) and five have over 1200 months of data (long stations). In fact over 40 of the medium station have over 720 months (or 60 years) of data which is fairly unusual. This is because there was a significant and abrupt increase in the number of weather station records in Poland in 1951. Similar investments in new stations are seen in many other countries as well in the latter part of the 20th century, but these tend to occur around 1960 or 1970-1973.

The locations of these long and medium stations are shown below in Fig. 50.2. The map indicates that the stations are fairly evenly distributed across Poland which means that a simple average of the anomalies from all these stations should approximate very well to the temperature trend for the country as a whole.

Fig. 50.2: The locations of long stations (large squares) and medium stations (small diamonds) in Poland. Those stations with a high warming trend are marked in red. 

 

In order to determine the mean temperature change for Poland, I first calculated the temperature anomalies for each temperature record relative to its monthly means (MRTs) for the period 1951-1980. These anomalies were then averaged to produce the trend shown in Fig. 50.3 below.

The 1951-1980 interval was chosen because it allowed the maximum number of stations to be included in the mean (see Fig. 50.4 below) while also avoiding the sudden jump in temperatures seen around 1988 in many European temperature records (see Post 44 and Post 49) that could destabilize the MRTs. For a moredetailed description of how the monthly reference temperatures (MRTs) are calculated and why, please refer to Post 47.

 

Fig. 50.3: The temperature trend for Poland since 1779. The best fit is applied to the interval 1811-2010 and has a positive gradient of +0.45 ± 0.08 °C per century. The monthly temperature changes are defined relative to the 1951-1980 monthly averages. 

While the trend in Fig. 50.3 above is the result of averaging over 60 separate records, no more than 58 are included in any single monthly average, and before 1950 this is typically less than ten (see Fig. 50.4 below). Overall, the temperature trend exhibits a significant warming of about 0.9 °C since 1800, but this is much less than that seen in the trend for Warsaw as shown in Fig. 50.1 above. The difference is almost certainly due to anthropogenic effects such as the urban heat island (UHI) effect or waste heat emissions from human and industrial activity. Overall such direct anthropogenic surface heating (DASH) would be expected to increase the temperature of the whole of Poland by about 0.2 °C.

The other detail that is noticeable about the data in Fig. 50.3 is that the temperatures in the 1930s were similar to those of today. This is despite temperatures appearing to have jumped suddenly by about 0.84 °C in 1988. A similar and larger jump of 0.97 °C was seen in the temperature data across Germany at the same time (see Post 49).

Fig. 50.4: The number of station records included each month in the mean temperature trend for Poland when the MRT interval is 1951-1980.

What is clear is that the warming seen in Poland, while significant, is much less than that expected based on IPCC and Berkeley Earth reports. These have suggested that the warming is over 1.5 °C and fairly monotonic. In reality there is a large amount of what looks like natural variation in the data that persists even for very long time-averaged data such as the 5-year moving average.

Fig. 50.5: Temperature trend in the Poland since 1779 derived by aggregating and averaging the Berkeley Earth adjusted data for all long and medium stations. The best fit linear trend line (in red) is for the period 1801-1980 and has a gradient of +0.32 ± 0.03 °C/century.

For comparison, the temperature trend that results from averaging the temperature data after it has been adjusted by Berkeley Earth is shown in Fig. 50.5 above. This trend shows a modest warming of 0.32 °C per century before 1980, or about 0.6 °C in total, followed by a major temperature increase of over 1 °C after 1980. This trend is also virtually identical to the one published by Berkeley Earth (see here) as shown in Fig. 50.6 below.

Fig. 50.6: The temperature trend for Poland since 1750 according to Berkeley Earth.

If we look at the difference between the mean trend in Fig. 50.3 (based on the original true data) and the trend in Fig. 50.5 that is the result of using the Berkeley Earth adjusted data we see that the adjustments made by Berkeley Earth are again not neutral. In fact the Berkeley Earth adjustments add nearly 0.6 °C of warming since 1840 (see Fig. 50.7 below).

Fig. 50.7: The contribution of Berkeley Earth (BE) adjustments to the anomaly data in Fig. 50.5 after smoothing with a 12-month moving average. The blue curve represents the total BE adjustments including those from homogenization. The linear best fit (red line) to these adjustments for the period 1841-2010 has a gradient of +0.335 ± 0.007 °C per century. The orange curve shows the contribution from breakpoint adjustments.

Conclusions

It is clear from the results shown here that temperatures in Poland have increased over the last 250 years, but by how much and for what reason remains unclear. There has certainly not been the catastrophic warming due to carbon dioxide emissions (i.e. more than 1.5 °C) that has been claimed by climate scientists, although there might have been some warming from this source. However, such warming cannot realistically be greater than 0.7 °C (i.e. the 0.9 °C seen in Fig. 50.3 minus the 0.2 °C we would expect from DASH or UHI effects). The problem is that any remaining warming that may be due to CO₂ emissions does not correlate well with CO₂ levels in the atmosphere over time. And then there is the uncertainty over the amount that natural variation in the temperature record may be contributing to the relatively short-term trends (less than 250 years) that we are observing.

We can probably claim with a fair degree of confidence that the data after 1950 in Fig. 50.3 is likely to be highly reliable as it is based on over 50 station records that are evenly spaced geographically (see Fig. 50.2). But this raises the question of what is causing the sudden jump in temperatures seen in 1988 which is also seen in other countries such as Germany (see Post 49).

For data before 1950, this is based on between about four and ten station records, at least back to 1830. The overall trend for 1831-1980 suggests a total temperature rise of only about 0.35 ± 0.15 °C, which is less than the standard deviation of the temperature fluctuations in the 5-year moving average for that period. This suggests that these temperature changes could be explained by natural variability.

Finally, it is apparent that once again there is a large discrepancy (0.6 °C) between any temperature rises seen in the raw data (see Fig. 50.3) and the rises claimed by climate scientists (see Fig. 50.5). This difference is largely due to adjustments made to the raw data by climate scientists (see Fig. 50.7).

49. Germany - temperature trends PARABOLIC

If any country in Europe were to exhibit the effects of anthropogenic global warming (AGW) and climate change, then you might expect that country to be Germany. Except that it doesn't.

There are over 135 sets of weather data for Germany that contain over 480 months of data (see here). Of these 34 are long stations with over 1200 months of data while the remainder I denote as medium stations. In fact ten temperature records have over 2000 months of data. This makes the temperature data for Germany some of the best available.

The geographical locations of these weather stations are indicated on the map below (see Fig. 49.1). This shows that both the long and medium stations are distributed fairly evenly, although there appear to be slightly fewer medium stations in the former East Germany. The stations are also differentiated according to the strength of their warming trend. Those with a large warming trend are marked in red, where a large trend is defined to be one that is both greater than 0.25 °C in total and also more than twice the uncertainty. 

The threshold of 0.25 °C is set equal to the temperature rise that one would expect in the EU as a whole due to waste heat or direct anthropogenic surface heating (DASH) due to human and industrial activity. In fact for Germany, based on its population, area and energy consuption, we would expect the temperature rise since 1700 due to DASH to be at least 0.6 °C (see Post 14), even without the effects of an enhanced greenhouse effect.

 

Fig. 49.1: The locations of long stations (large squares) and medium stations (small diamonds) in Germany. Those stations with a high warming trend are marked in red.

 

The longest data set is for Berlin-Tempelhof (Berkeley Earth ID: 155194) which has data that extends back to 1701. This data is shown in Fig. 49.2 below as the temperature anomaly after subtracting the monthly reference temperatures (MRTs) based on the 1971-2000 averages. The method for calculating the anomalies and MRTs from the raw temperature data is described in Post 47. However, there are two caveats that need to be applied to the data in Fig. 49.2. Firstly, there are significant gaps in the data before 1756, and secondly any data before 1714 needs to be treated with caution simply because thermometers did not exist then, at least not in their current form. 

Fig. 49.2: The temperature trend for Berlin-Tempelhof since 1700. The best fit is applied to the interval 1821-1980 and has a positive gradient of +0.13 ± 0.10 °C per century. The monthly temperature changes are defined relative to the 1971-2000 monthly averages.

In order to determine the temperature trend for Germany I have averaged the temperature anomalies from all 135 long and medium stations. The result is shown in Fig. 49.3 below. All stations with data less than 480 months are excluded as they add no real value to the result, particularly if the data is very recent (i.e. after 1980). This is because the temperature change over time is small, typically 1 °C per century, so you really need at least 40 years of data to detect a measurable trend above the noise.

Fig. 49.3: The temperature trend for Germany since 1700. The best fit is applied to the interval 1756-2005 and has a negative gradient of -0.02 ± 0.05 °C per century. The monthly temperature changes are defined relative to the 1971-2000 monthly averages.

What is immediately apparent is that the trend in Fig. 49.3 differs significantly from the widely publicized IPCC version. Firstly, temperatures before 1850 appear to be higher than they are now, not lower. Secondly, temperatures were stable or declining for over 150 years prior to 1980, not rising. And finally, the mean temperature appears to jump suddenly in 1988 just as the IPCC was being established. Some of these traits are also seen in the mean temperature trend I constructed for the whole of Europe that was published in Post 44. The 19th century cooling is also seen in the temperature data of New Zealand (see Post 8) and Australia (see Post 26).

 

Fig. 49.4: The amount of temperature data from Germany included in the temperature trend each month for three different choices of MRT interval.

As I pointed out in Post 47, the choice of interval for determining the MRTs can influence the number of station records that are included in the final average for the temperature trend, and thus can also influence the nature of the trend itself. In order to test how robust the trend in Fig. 49.3 is regarding changes to the MRT interval, I repeated the calculation for three different MRT intervals. The curves in Fig. 49.4 above show how the number of stations in the final trend changes for each of the different MRT intervals. 

It is clear that there is very little difference between choosing MRT intervals of 1956-1985 and 1971-2000, although the latter does result in a slightly larger number of stations being included in the trend calculation after 1960. The advantage of using the former interval is that it corresponds to a part of the temperature record where the mean temperature is fairly stable whereas the latter interval spans the abrupt increase in temperature seen around 1988. Despite this, in both cases the final trends are very similar, with the best fit in each case being -0.015 °C/century for the 1971-2000 MRT and -0.032 °C/century for the 1956-1985 MRT. In both cases the fitting range was 1756-2005.

The 1901-1930 interval enables more data from before 1930 to be included in the trend (from stations that were closed down before 1930), but significantly less after 1950 when many new stations were set up. Nevertheless, the final trend is almost identical to the those for other two MRT intervals with the best fit being only slightly higher at +0.0004 °C/century. In all three cases temperatures before 1850 were about as high as those after 2000, and in all three cases the mean temperature trend exhibited a large jump in temperature in 1988 as is shown clearly in the 5-year moving average in Fig. 49.3.

Fig. 49.5: The temperature trend for Germany since 1750 according to Berkeley Earth.

Irrespective of which interval is used to determine the MRTs, the resulting temperature trend I have constructed and published in Fig. 49.3 differs significantly from that published by Berkeley Earth which is shown in Fig. 49.5 above. The difference, as I have noted before, is due to homogenization and breakpoint adjustments used by Berkeley Earth to create their adjusted anomalies for each station. Averaging their adjusted anomalies yields the trend shown below in Fig. 49.6, which is virtually identical to the one shown above in Fig. 49.5. This demonstrates that it is not a difference in averaging method that is responsible for the difference between my results in Fig. 49.3 and the Berkeley Earth result. So it must be a difference in the anomaly data itself that is responsible. This can only be due to the adjustments made by Berkeley Earth.

Fig. 49.6: Temperature trend in Germany since 1750 derived by aggregating and averaging the Berkeley Earth adjusted data for all long and medium stations. The best fit linear trend line (in red) is for the period 1801-1980 and has a gradient of +0.29 ± 0.03 °C/century.

The actual temperature difference between the data in Fig. 49.6 and that in Fig. 49.3 is shown below in Fig. 49.7 (blue curve) as the the total adjustment made to the data by Berkeley Earth. The data in Fig. 49.7 highlights two points of note. Firstly, the Berkeley Earth adjustments are not neutral: they add about 0.3 °C to the warming after 1840. Secondly, the adjustments flatten the curve before 1840 and so remove the warm period that mirrors the one seen after 1988. In so doing these adjustments radically change the nature of the temperature trend from an oscillatory one in Fig. 49.3 to the infamous hockey stick shape in Fig. 49.6 that is now synonymous with anthropogenic global warming (AGW).

Fig. 49.7: The contribution of Berkeley Earth (BE) adjustments to the anomaly data in Fig. 49.6 after smoothing with a 12-month moving average. The blue curve represents the total BE adjustments including those from homogenization. The linear best fit (red line) to these adjustments for the period 1841-2010 has a gradient of +0.173 ± 0.003 °C per century. The orange curve shows the contribution from breakpoint adjustments.

Conclusions

The results I have presented here clearly show that the real temperature trend for Germany over the last 300 years differs significantly from the conventional view of global warming. These differences can be summarized as follows.

1) Temperatures before 1840 were comparable to those of today (see Fig. 49.3).

2) The overall temperature trend since 1800 is broadly flat (see the best fit line in Fig. 49.3). 

3) At least 0.6 °C of any temperature rise since 1700 should be due to direct anthropogenic surface heating (DASH) or waste heat from human activity, and not from greenhouse gas emissions.

4) There is a large and seemingly unnatural temperature rise of 0.97 °C in 1988 that occurs at the very moment the IPCC is being formed (see the 5-year mean in Fig. 49.3).

5) Berkeley Earth adjustments have added 0.3 °C of warming to the temperature trend since 1840 and erased most of the warm temperatures before 1840 (see Fig. 49.7).

6) Of the 1.5 °C of warming since 1750 claimed by Berkeley Earth (see Fig. 49.6), 0.6 °C could be due to DASH (see point 3 above) and 0.3 °C is due to adjustments made to the temperature data by Berkeley Earth (see point 5 above).

48. Denmark - temperature trends STRONG WARMING 1.8°C

In total, Denmark has twenty-two sets of temperature data that exceed 480 months in length (see here). Of these, eight contain over 1200 months of data (long stations), with the longest being Copenhagen (Berkeley Earth ID: 154574) which has continuous data from 1798, and some data fragments that go as far back as 1768. This suggests that the country has a similar number of station temperature records as New Zealand (see Post 8), but surprisingly it is less than is found for the Danish autonomous territory of Greenland which has a population of less than 60,000 and which I will look at in detail at some point in the future.

Fig. 48.1: The locations of long stations (large squares) and medium stations (small diamonds) in Denmark. Those stations with a high warming trend are marked in red.

The distribution of these weather stations in Denmark is indicated in Fig. 48.1 above. It shows a fairly even spread that covers most of the country. It also shows that most of the station data exhibits some significant degree of warming, with only two stations exhibiting a cooling trend (defined as being a trend that is less than twice the uncertainty in the trend).

The data from Denmark is interesting in one other respect in that, of its fourteen medium length station temperature records (i.e. those with over 480 months of data but less than 1200), four have no data after 1970 but do have data going back to the 19th century, while six have no data before 1970. This means that these two groups of stations require different time periods for the calculation of the reference temperatures needed to find their monthly temperature anomalies. For an explanation of the rationale and process used to determine the temperature anomalies via the calculation of monthly reference temperatures (MRTs), please refer to my previous post.

 

Fig. 48.2: The maximum amount of temperature data available from Denmark each month for inclusion in the mean temperature trend.

This problem is illustrated in Fig. 48.2 above. The two peaks in the frequency distribution indicate the two different possibilities for the MRT period. As I pointed out in Post 47, ideally the MRT period needs to be about 30 years in length with at least 40% data coverage. One way to circumvent this problem is to calculate the temperature trend for two MRT time intervals (the data in Fig. 48.2 suggests that 1891-1920 and 1971-2000 should be optimal), compare the results, and if necessary take a weighted average. 

 

Fig. 48.3: The temperature trend for Denmark since 1750. The best fit is applied to the interval 1851-2000 and has a positive gradient of +1.18 ± 0.09 °C per century. The monthly temperature changes are defined relative to the 1971-2000 monthly averages.

If we choose 1971-2000 as our reference period for the MRTs, then the overall temperature trend is as shown in Fig. 48.3 above. The number of stations included each month in this overall trend is shown in Fig. 48.4 below. Overall, up to seventeen stations are included, but before 1970 that drops to less than ten with only one station with data before 1870. The result is that there appears to be a fairly continuous warming trend from 1851 to 2000 as indicated by the data in Fig. 48.3.

Fig. 48.4: The number of sets of station data included each month in the temperature trend for Denmark when the MRTs are calculated for the period 1971-2000.

Now consider what happens if we choose 1891-1920 as our reference period for the MRTs. The result is that there are more stations included before 1970, but less after (see Fig. 48.5 below). This also changes the form of the temperature trend in Fig. 48.6.

Fig. 48.5: The number of sets of station data included each month in the temperature trend for Denmark when the MRTs are calculated for the period 1891-1920.

What we now see in Fig. 48.6 is a much smaller warming trend before 1980 (less than 0.6 °C with possibly higher temperatures before 1800), but a more pronounced jump in temperatures after 1988. This similar to the trend seen for South Africa (see Post 37) and also for Europe as a whole (see Post 44). It is important to note, though, that all the data before 1860 in both Fig. 48.6 and Fig. 48.3 comes from just one station record: Copenhagen (Berkeley Earth ID: 154574). This means the accuracy and reliability of this data cannot be truly ascertained.

Fig. 48.6: The temperature trend for Denmark since 1750. The best fit is applied to the interval 1768-1980 and has a positive gradient of +0.30 ± 0.05 °C per century. The monthly temperature changes are defined relative to the 1891-1920 monthly averages.

The analysis outlined above means that we have two possible results for the temperature trend in Denmark. Both are fairly similar, and for once both are in general agreement with the trend published by Berkeley Earth (see Fig. 48.7 below). But can we combine them into a single result?

Fig. 48.7: The temperature trend for Denmark since 1750 according to Berkeley Earth.

The answer is yes. If we take the weighted average of each of the two trends in Fig. 48.3 and Fig. 48.6 we get the result shown in Fig. 48.8 below. The relative weightings of each month's data is determined by the number of stations included in the average for that month as indicated in Fig. 48.4 and Fig. 48.5 respectively. There is, though, one other factor we need to take into account: the different MRT intervals for the two original trends. Without a correction term this will distort the final data.

In order to allow for the differing MRTs, the trend curve in Fig. 48.3 needs to be first adjusted upwards so that the mean temperature anomaly for the period 1891-1920 is zero in order to be consistent with the data in Fig. 48.6. This requires an upward adjustment of 0.634 °C. Only after this adjustment has been made can the weighted average be determined.

Fig. 48.7: The weighted temperature trend for Denmark since 1750. The best fit is applied to the interval 1851-2000 and has a positive gradient of +1.02 ± 0.09 °C per century. The monthly temperature changes are defined relative to the 1891-1920 monthly averages.

Conclusions

The data from Denmark appears to show a warming trend of about 1.5 °C since 1850. This is by far the largest warming seen in any of the regional records that I have investigated so far. It is also one of the few that appears to agree with IPCC reported values. However, this is not as straightforward as it seems. For a start changing the MRT interval from 1971-2000 (as in Fig. 48.3) to 1891-1920 (as in Fig. 48.6) dramatically reduces the temperature trend before 1980. So which one is correct? 

Then there is the problem of the sudden jump in temperature in 1988 of 0.93 °C. A similar jump was seen in the temperature trend for the Europe data in Post 44 as well. The reason for this is still unclear (at least to me). In Post 45 I speculated that it could be the result of improved air quality in Europe due to EU legislation. Alternatively, it could be the consequence of a change in measurement method, such as a change from liquid-in-glass thermometers to electronic systems which occurred around that time. What is strange is the timing and suddenness of this increase. 

Whatever the true scale of the temperature rise in Denmark since 1750, it cannot be explained entirely by direct anthropogenic surface heating (DASH) or waste heat. The best estimate of the expected magnitude of DASH for Denmark (based on its population density) is about 0.35 °C since 1850. However, this could be greater if the source of the heating from human industrial activity is concentrated around the locations of the major weather stations. For example, a city like Greater London with an area 1569 km² consumes over 132 TWh of energy each year. This equates to a power density of 9.6 W/m², or an effective temperature rise of over 4 °C. Clearly something similar but less extreme could be occurring around the major cities in Denmark, but at the moment, without direct measurement data, that remains as speculation.

47. Calculating the monthly anomalies using MRTs

Over the next few posts I intend to return to my investigation of the temperature records in Europe by extending my analysis to other countries of the EU besides those of Belgium and the Netherlands that were studied in Post 40 and Post 41 respectively. Central to all these studies is the concept of the temperature anomaly. In many of my previous posts (including Post 4) I have given explanations of how these have been calculated. However, because the data for each country or region tends to have different temporal distributions of data, this has sometimes necessitated using slightly different methods for determining the anomalies of some countries compared to others. So, as this is the start of a new year, I thought this would be a good time to outline exactly how the anomalies are derived, and what drives the decisions to change the methodology from time to time.

The process I use is broadly similar to that used by the main climate science groups (i.e. NOAA, NASA-GISS, Hadley-CRU and Berkeley Earth). However, there are a number of differences, and given how important the analysis process is in terms of its impact on the resulting temperature trend, it therefore seems important that I describe explicitly what I do, and why I do it, not least so that it can be easily referenced in the future.

When studying climate change it is essential that we are able to compare temperature data from different epochs and different locations. There are essentially two problems here. The first is that not all temperature records are of the same length (in terms of time). The second is that the temperatures from different regions can have massively different mean values and ranges of temperature fluctuation.  

For example, Europe has over 100 temperature records that predate 1850 and have over 1800 months of temperature data. The whole of the Southern Hemisphere has two (Rio de Janeiro and Hobart). 

When it comes to temperature ranges and mean values, there are similar extremes. Station records from near the equator (such as Manaus) can have very high mean temperatures of +27 °C with the monthly mean only varying by about ±1 °C across the seasons (such as they are). In contrast, at the South Pole the mean temperature is about -48 °C and the variation of the monthly mean over the year can be ±15 °C or more.

If all temperature records were of the same length, and if all regions of the planet had the same number of stations, these differences would not matter. But because records have different lengths and are often clustered in certain regions, they do. To see how, consider the following.

i) The mathematical basis of the temperature anomaly

In an ideal world we could calculate the change in temperature just by averaging all the temperatures from all the different stations for a given month. If this average was different from month to month then that would be evidence of climate change. We can represent this mathematically as follows.

If T_i(m) is the mean temperature of station i for month m, and M_i is the mean temperature of station i over all time, then

 T_i(m) = M_i + ε_i(m) 

(47.1)

where ε_i(m) is the variation of the monthly mean temperature for station i for each different month m (see Post 5 for more explanation of temperature anomalies, weather and climate). The index m has a different integer value for each month of data in the temperature record for that station. So, if the temperature record has 1200 months of data, m will take values from 1 to 1200. 

The term ε_i(m) in Eq. 47.1 is the temperature anomaly. It is the amount by which the temperature in station record i varies from a reference value, usually taken to be the long term mean temperature, M_i. Now consider what happens when we sum the temperatures for month m from all i station records.

 ∑_i T_i(m) = ∑_i M_i + ∑_i ε_i(m) 

(47.2)

If we now calculate the average of each term we get the result

 <T(m)> = <M> + <ε(m)>

(47.3)

where <T(m)> is the mean of T_i(m) averaged over all i stations, and repeated for each month m. Similarly, <ε(m)> is the mean of ε_i(m) averaged over all i stations for each month m, and <M> is the mean of M_i averaged over all i stations for each month m. 

In an ideal world where all temperature records have valid data in each given month m, the term <M> is just a constant that does not vary with the month m. It then follows that the change in the mean temperature <T(m)> from month to month m will be the same as the change in the anomaly <ε(m)> from month to month. So, in an ideal world (where all temperature records are of the same length), averaging all station temperature records should give us the climate change over time.

But we don't live in an ideal world and all temperature records are not of the same length. This means that <M> will not be the same for every month, but will generally be different for different months, depending on how many of the temperature records have data for that month and how many don't. So <M> will vary from month to month. That means it will contribute to (and possibly dominate) the temperature trend over time, and consequently this means that we can't use the average of all temperatures <T(m)> to determine the temperature change over time. Instead we have to use the average of the anomalies for each month <ε(m)>. That in turn means we need a reliable way of calculating the anomalies.

ii) Defining the temperature anomaly

The anomalies are the amount by which the temperatures in a given temperature record deviate from a reference value. That reference value is usually taken to be a mean of the monthly temperature data over a particular time interval. Ideally that time interval should be as long as possible so that it is as accurate as possible. However, there are two problems here. 

The first is that, if the temperature records have a strong trend, either upwards or downwards, and you use different time periods to calculate the reference mean temperature of the different records, this will distort the mean temperature trend, particularly if the different temperature records have differing amounts of data. So you really need to use the same time period for all temperature records when calculating their reference temperatures. That means that you generally can't use extremely long time time periods that use all the data from that record, but instead must use shorter time periods (usually 20 or 30 years) for which as many station records as possible have sufficient data. And if a particular temperature record has no data or insufficient data in that time period (say for the period 1961-1990) when many other records do, then that record will have to be excluded from the calculation of the mean temperature trend. If a significant number of long datasets are excluded in this way, then there are ways of repeating the calculation of the mean reference temperature using other time periods in order to include them, but that is a subsidiary problem. Essentially you will end up with multiple mean temperature trends which could then be merged into a single trend through a weighted averaging process based on the number of station records incorporated into each one.

The second problem is that as you move away from the equator, the seasonal variation of the mean temperature increases. As I pointed out above, near the equator typical variations of the mean temperature each month can vary by as little as ±1 °C. However, at latitudes of 50°N (i.e. in Europe or North America) typical variations of the mean temperature each month can exceed ±10 °C. This means that it is more accurate to calculate a mean temperature for each month (so twelve in total), rather than just calculating one overall. These mean temperatures I have referred to in previous posts as the monthly reference temperatures or MRTs.

iii) Choosing a time-frame for the MRTs

In order to determine the temperature trend for a country or region you need to average the temperature anomalies from all of its temperature records. So you need to first calculate the anomalies for each station record. In order to calculate the temperature anomalies you need to first calculate the monthly reference temperatures or MRTs for all twelve months of the year for that record. However, in order to do this with the minimum amount of statistical error you need to consider a number of factors that may influence how you choose your reference period for the MRTs.

The first thing you need to ensure is that the MRTs are calculated over the same time-frame for each temperature record. The reason for this is the the same as was expounded in (ii) above. If the temperature records are of differing lengths, then using different MRTs for each one will have the same effect as using different values of <M> for each month in Eq. 47.3. It will distort the mean temperature trend.

Next, you want the time-frame you use to calculate the MRTs to be as long as possible so that it is as accurate as possible. Unfortunately, because the majority of temperature records tend to be fairly recent with less than 40 years of data, this means that you will lose accuracy in your mean temperature trend due to insufficient temperature records qualifying for the averaging process.

So in order to incorporate as much of the available temperature data as possible into the final mean temperature trend you need to reduce the time-frame, but not reduce it so much that the MRTs are no longer sufficiently accurate. This is basically a compromise between maximizing the time-frame you use for the MRT calculations, and maximizing the amount of data that can then be used in the mean temperature trend calculation. The most effective way to do this is to create a frequency histogram for each month m, where the value for each month is the sum of all the record lengths for station data that have valid data for that month m. So if temperature record i has L_i months of data, and δ_i(m) is a binary function for station i that takes the value 1 if month m in record i has valid data and 0 if it does not, then the monthly data frequency function f(m) will be

 f(m) = ∑_i L_i δ_i(m)

(47.4)

An example of such a frequency function is shown below in Fig. 47.1 for data from the Netherlands. The peak in the distribution indicates where a time-frame chosen to determine the MRTs is likely to generate the maximum amount of anomaly temperature data for inclusion in the mean temperature trend.

 Fig. 47.1: The amount of temperature data available from the Netherlands when each month is included in the MRT.

 

The data in Fig. 47.1 above suggests that the optimal 30-year time-frame that allows the most data to be included in the final trend is likely to be around 1975-2010. In fact the time-frame 1976-2005 was eventually chosen (see Post 41). However, there are two other considerations that need to be taken into account before finally settling on a time-frame. 

Ideally you want the overall temperature trend for your time-frame to be close to zero. This is to improve accuracy in the MRT calculations. Unfortunately that is not always possible. In fact it rarely is. This is because the majority of data in most temperature data tends to be fairly recent, as illustrated in Fig. 47.1, but recent data also tends to exhibit the greatest warming trend.

The final problem is the issue of missing or incomplete data. Even some of the best temperature records will have several months of missing data within your chosen MRT time-frame. The way to address this is to set minimum thresholds for the number of months of data that need to be present within the MRT time-frame in order for data from that station to be included in the mean temperature trend.

Based on the above conditions I have generally used the following criteria to determine the MRTs.

1) Select a time-frame of 30 years where there is the most data available. Failing that use a 20 year time-frame.

2) For each of the 12 monthly MRTs, only calculate the MRT if there is at least 40% of the data available within the time-frame (i.e. 12 out of 30 years). For a 20 year time frame increase this to 60% (i.e. 12 out of 20 years). 

3) If the MRT cannot be determined for any of the 12 months in a given record, then all data for that month of the year from that record is excluded for all years.

iv) Calculating the MRTs and the anomalies

The MRT for each month of a given record is calculated by first determining the time-frame for its calculation as set out above in (iii), and then averaging all the available temperature readings for that month within the time-frame. 

To see how this works in practice, consider the case of the temperature record from Volken (Berkeley Earth ID: 92832) in the Netherlands. We have already seen in Fig 47.1 above that the optimal time-frame for calculating the MRTs in the Netherlands is around 1976-2005. This will be the same for all station records in the region. The mean monthly temperatures for Volken are shown in Fig. 47.2 below with data in the MRT reference period (1996-2005) shown in yellow.

 

Fig. 47.2: The raw monthly temperature data for Volken with the data in the MRT time-frame highlighted in yellow.

 

We next find the mean temperature values for each of the twelve months January-December using the yellow data in Fig. 47.2 above. These mean temperatures are listed in Table 47.1 below. These are the MRT values described above.

 

Table 47.1

Month	Mean Temperature or MRT (°C)
January	2.4818
February	2.9020
March	6.0305
April	8.6293
May	12.9136
June	15.5573
July	17.5369
August	17.4261
September	14.3748
October	10.6354
November	6.0696
December	3.4268

The MRT values are then subtracted from the raw data in Fig. 47.2 to yield the anomalies for each month. This is shown in Fig. 47.3 below, where the MRTs are plotted repeatedly in green and the anomalies are in red. It therefore follows that adding the red curve in Fig. 47.3 to the green curve in Fig. 47.3 will recreate the original data in Fig. 47.2.

 

Fig. 47.3: The MRT values and the temperature anomalies for Volken.

In the next few posts I will look at the temperature data for a number of different countries in Europe. In each case the temperature anomalies for each station will be calculated using the method outlined here. The most significant differences in the method used from country to country will be in the choice of MRT time-frame (this will normally be 1961-1990 but may be later or earlier) and the length of the time-frame (normally 30 years, but sometime 20 years will be required due to a lack of available data). In each case this will be indicated, as will the reasons for the choices.