16. The story so far

 

The main purpose of this blog has been to analyse the physics behind climate change, and then to compare what the basic physics and raw data are indicating with what the climate scientists are saying. These are the results so far.

Post 7 looked at the temperature trend in New Zealand and found that the overall mean temperature actually declined until 1940 before increasing slightly up to the present day. The overall temperature change was a slight rise, but only amounting to about 0.25 °C since the mid 19th century. This is much less than the 1 °C rise climate scientists claim.

Post 8 examined the temperature trend in New Zealand in more detail and found that the breakpoint adjustments made to the data by Berkeley Earth, that were intended to correct for data flaws, actually added more warming to the trend than was in the original data.

Post 9 looked at the noise spectrum of the New Zealand data and found evidence of self-similarity and scaling behaviour with a fractal dimension of about 0.25. This implies that long-term temperature records over several thousands of years should still see fluctuations between the average temperature each century of over 0.5 °C, even without human intervention. In other words, a temperature rise (or fall) of at least up to 1 °C over a century is likely to be fairly common over time, and perfectly natural.

Post 10 looked at the impact of Berkeley Earth's breakpoint adjustments on the scaling behaviour of the temperature records and found that they had a negative impact. In other words the integrity of the data appeared to decline rather than improve after the adjustments were made.

Post 11 looked at the degree of correlation between pairs of temperature records in New Zealand as a function of their distance apart. For the original data a strong linear negative trend was observed for the maximum possible correlation between station pairs over distances up to 3000 km. But again the effect of Berkeley Earth's breakpoint adjustments to the data was a negative one. This trend became less detectable after the adjustments had been made. The one-year and five-year moving average smoothed data did become more highly correlated though.

After analysing the physics that dictate how the Sun and the Earth's atmosphere interact to set the Earth's surface temperature in Post 13, I then explored the implications of direct heating or energy liberation by humans at the Earth's surface in Post 14. Calculations of this direct anthropogenic surface heating (DASH) showed that while human energy use only contributed an average increase of 0.013 °C to the current overall global temperature, this energy use was highly concentrated. It is practically zero over the oceans and the poles, but in the USA it leads to an average increase of almost 0.2 °C. This rises to 0.3 °C in Texas and 0.5 °C in Pennsylvania. Yet in Europe the increases are typically even greater. In England the increase is almost 0.7 °C, and in the Benelux countries almost 1.0 °C. Perhaps more significantly for our understanding of retreating glaciers, the mean temperature rise from this effect for all the alpine countries is at least 0.3 °C.

Finally in Post 15 I looked at the energy requirements for sea level rise (SLR). Recent papers have claimed that sea levels are rising by up to 3.5 mm per year while NOAA/NASA satellite data puts the rise at 3.1 mm per year. These values are non-trivial but are still a long way short of the rate needed to cause serious environmental problems over the next 100 years.

In upcoming posts I will examine more of the global temperature data. But given what I have discovered so far, it would be a surprise if the results were found to be as clear cut as climate scientists claim. Contrary to what many claim, the science is not settled, and the data is open to many interpretations. That is not to say that everything is hunky dory though. Far from it.

15. The truth about sea level rise

One of the most emotive and alarmist claims made by climate scientists is that global warming will lead to a catastrophic sea level rise (SLR) that will submerge major cities and lead to an unprecedented humanitarian crisis and global extinction event.

Fig. 15.1: Britain's favourite polar bear - Peppy.

On the face of it this seems quite plausible, even likely. We see images of collapsing ice shelves and retreating glaciers on an almost daily basis. We see icebergs the size of cities being calved off from Antarctica and then polar bears looking forlorn on icebergs the size of a lifeboat, like something from a Fox’s glacier mint advert. So what is the reality?

Fig. 15.2: Life imitating art.

There are two principal ways that sea levels might change: either the amount of water in the sea changes, or the existing sea water changes its density. The former can happen if ice caps on Greenland or Antarctica melt. It cannot happen through the melting of sea ice because of Archimedes' Principle as I explained in Post 2, nor for the same reason can an increase in sea ice change the sea level. One alternatively mechanism is through increased evaporation of condensation, but that requires the humidity of the atmosphere to change. As for density changes, these are governed mainly by changes in the temperature of the sea water.


Scenario 1: Thermal Expansion

In the case of rising sea temperatures it is not the current global temperature that is important per se, but the temperature history and the thermal budget of the Earth. Global temperature rises can only raise sea levels directly (excluding from ice melting) by thermal expansion of the sea water. As I pointed out in Post 2, the coefficient of thermal expansion by volume for water is 0.000207 per degree Celsius or 207 ppm/°C. So a column of water 1000 metres or 1 km high will increase in height by only 20.7 cm if its temperature increases by 1 °C (or 1 K where K is the unit of absolute thermodynamic temperature - the kelvin).

But there is another factor we need to consider - the total heat or thermal energy required to do this. This is because this energy needs to come from somewhere, and once used it remains trapped in the water. It is, therefore, energy that has been sequestrated, the effect of which is to create an imbalance between the amount of energy the Earth receives from the Sun, and the amount it emits back out into space. This difference can only come from the net energy imbalance of the Earth’s energy budget.

In the last post we saw that this imbalance is currently estimated to be as much as (and no-one is saying it is more than) 0.9 W/m². If this figure is true (and as I pointed out, there is enormous uncertainty over its accuracy), and if it had been constant over the last 100 years (which is very unlikely), it would imply that the Earth has absorbed a total of 4.591x10¹⁴ joules of energy every second in that time period, or 1.45 x 10²⁴ J in total. Of course that is the upper limit of what is likely. No-one seriously thinks the Earth’s energy imbalance has always been 0.9 W/m². So the average over the last 100 years must be considerably less, and probably less than half.

Whatever the value, though, this heat will increase the temperature of the oceans. The question is, by how much, or to what depth?

As the specific heat capacity of water is 4200 Jkg^-1K^-1, the amount of energy required to heat 1 kg of water by 1 K (or 1 °C as these temperature changes are the same) will be 4200 J. If our 1 km high water column has a cross-section of 1 m², then it will contain 1000 tonnes of waters. Therefore, the total energy required to raise the temperature of the entire column by 1 °C will be 1,000,000 times greater than 4200 J, in other words 4.2 x 10⁹ J. As 70.8% of the Earth’s surface is covered by the oceans, the total volume of water down to a depth of 1 km will be 3.61 x 10¹⁷ m³. The total mass will be 3.61 x 10²⁰ kg, and the total heat capacity will be 4200 times higher still at 1.52 x 10²⁴ J/°C. So the mean temperature rise of the oceans down to a depth of 1 km over then last 100 years will be (at the absolute maximum) 1.45 x 10²⁴ ÷ (1.52 x 10²⁴) = 0.95 °C.

So, if we assume that the Earth’s energy imbalance over the last 100 years has been 0.9 W/m² everywhere and at all times, and if we assume that this heat has all ended up in the ocean, and it has heated the top 1000 m only, then the temperature rise of that top layer of water will be 0.95 °C. Some may find this number suspiciously close to the value claimed for global warming of about 1 °C per century. In other words, that climate scientists have worked backwards. They have assumed that the oceans must heat up by the same amount as the land over the same period, and to a depth of up to 1000 m, and worked out the amount of heat required to do this. From this they have inferred an imbalance in the Earth’s thermal budget rather than measured it.

Whatever the sequence of events, the resulting sea level rise (SLR) will be 197 mm (i.e. 0.95 x 207). If the warming layer of the ocean is thinner (say 500 m) but the surface energy imbalance is still 0.9 W/m², its mean temperature rise will be greater (an unlikely 1.90 °C for a 500 m thick layer), but the SLR will be the same, in other words a massive 1.97 mm per year. So what is clear is that the maximum sea level rise that can occur depends on the energy imbalance and not the water depth. In reality, the surface energy imbalance may be less than 0.9 W/m² (G. L. Stephens et al., Nature Geoscience 5, 691–696 (2012) suggest 0.6 W/m² as I pointed out in Post 13) and has in all likelihood got worse over time. So while it may be 0.9 W/m² now, it has probably averaged less than half of 0.9 W/m² over the last 100 years as global temperatures have risen. In which case the SLR has probably been less than 100 mm over the last century (or less than 66 mm if Stephens et al. are correct). But what about the future?

Assuming that the surface energy imbalance remains at 0.9 W/m² for the foreseeable future, and if we now assume that only that portion of the surface energy imbalance over the oceans is actually absorbed by the oceans, then the heat absorbed by the oceans each year will be 28.4 MJ/m². If this were absorbed by a column of water 1000 m deep it would result in a temperature rise of 6.76 mK. If it were instead absorbed by a column of water only 100 m deep it would result in a temperature rise of 67.6 mK. Either way, the resulting thermal expansion would be 1.40 mm per year. Even over 100 years this is a long way short of the 10 m rise some doom-mongers are projecting, and on its own is unlikely to pose a major threat to human civilization or the planet.

But thermal expansion is just one component of the overall problem, because not all the 0.9 W/m² (or 0.6 W/m²) need end up in the oceans. Some may instead end up melting the ice caps.


Scenario 2: Melting Ice Caps

In this scenario there are a number of factors that we need to identify and address. Firstly, where is the ice? If it is floating on the ocean surface then it cannot add to the sea level increase when it melts, despite 9% of the ice being above the water line. This is because of Archimedes’ principle as I explained in Post 2. It can, though, sequestrate energy and actually reduce warming elsewhere. The only ice that can increase sea levels when it melts is ice that is on land. This is found mainly on Greenland (3 million cubic kilometres) and Antarctica (30 million cubic kilometres).

Then there is the question of the ice temperature. Before it can melt it needs to be heated to 0 °C, yet the mean temperature of the ice on Antarctica is about -50 °C. In order to raise the ice temperature to melting point would require 3.20 x 10²⁴ J of energy (the specific heat capacity of ice is 2108 Jkg^-1K^-1 and its relative density is 0.92).

Next, you need to melt the ice. This will require an energy input of 1.01 x 10²⁵ J (the specific latent heat of ice is 332 kJ/kg); and then you need to heat it to the ambient temperature of the Earth, about 15 °C, otherwise it will cool the oceans and your global temperatures will go down. This requires another 1.91 x 10²⁴ J of energy. So the total energy required is 1.52 x 10²⁵ J. Given that the amount of power available to achieve this is at most only 0.9 W/m², that means it would take at least 1100 years to occur. But even that assumes that all the power from the Earth’s energy imbalance could be channelled somehow into melting the ice caps and nothing else.

In reality most will initially go into the oceans. As Antarctica and Greenland comprise only 3% of the Earth’s surface area, a more realistic estimate is that it would take up to 30,000 years, by which time we would be in the next ice age. Recent studies of Greenland appear to confirm this as they show Greenland has lost less that 0.05% of its ice in the last 10 years, but this may just be cyclical. 

One final point of note: while the total volume of ice on Antarctica is 30 million cubic kilometres, almost a third of this is below sea level. The net result is that if all the ice on Antarctica and Greenland were to melt, sea levels would rise by 65 metres not 91 metres. Yet over 30,000 years this will amount to a rise of only about 2 mm per year.


Scenario 3: Evaporation

The final possibility is that the sea water might just evaporate into the atmosphere leading to a loss of volume in the sea rather than a gain. Approximately 0.4% of the atmosphere by volume is water vapour. But if all this water were to suddenly condense out of the atmosphere it would only add 3.6 cm to the depth of the oceans. Given that the ambient temperature at the surface of the Earth is 15 °C, while the humidity at 0 °C would be expected to drop to near zero, this suggests that an increase of 1 °C in the surface temperature of the air would lead to a decrease in sea levels of around 2.4 mm. That is a pretty crude estimate, though, and assumes that the vapour pressure of water increases proportionately with temperature from its freezing point. A more accurate estimate can be made using the Clausius-Clapeyron equation.

Fig. 15.3: Schematic of phase boundaries on a P-T diagram.

This equation (see Eq. 15.1) relates the the slope of a phase boundary in a pressure-temperature diagram to the thermodynamic temperature, T, the molar latent heat for the phase change, L, and the change in molar volume across the boundary ∆V. An example of a phase diagram is shown in Fig. 15.3 above.

(15.1)

For a change from liquid to gas (as in evaporation) the term ∆V should be the difference in molar volumes between the water in the liquid phase and the vapour in the gas phase. However, as the volume of the vapour at the relevant pressures we are likely to encounter (i.e. around atmospheric pressure) is so much greater than it is for water (in fact by more than a factor of 1000) we can use the ideal gas law in Eq. 15.2 to substitute the molar volume of water vapour V for ∆V on the basis that the molar volume of the liquid is negligible.

(15.2)

In Eq. 15.2 the term V is the volume of one mole of water vapour at a pressure P and a temperature T. The term R is the molar gas constant where R = 8.314 Jmol^-1K^-1 and n is the molar density in mol/m³. The approximation of V for ∆V allows us to make a substitution from Eq. 15.2 into Eq. 15.1 to generate Eq. 15.3 which is now a function of only two variables, P and T.

(15.3)

This allows us to relate fractional changes in the pressure of the gaseous phase to fractional changes in temperature along the phase boundary. The differential in Eq. 15.3 implies that for small changes in P and T the following relation holds

(15.4)

while Eq. 15.2 yields the following relation between P, T and n.

(15.5)

Equating Eq. 15.4 with Eq. 15.5 gives the result for the fractional change in molar concentration of the vapour that will occur due to  evaporation across the phase boundary for a temperature change ∆T.

(15.6)

The relation in Eq. 15.6 allows us to estimate the change in water vapour concentration n as the temperature T changes. So for example, if the temperature T = 288 K and the latent heat of evaporation of water is 40.8 kJmol^-1K^-1, then a temperature rise of ∆T = 1 K will yield a fractional change of water vapour concentration of 0.0557. That in turn implies a total fall in sea level over the period of the temperature rise (which is about 100 years) of 2.0 mm (= 0.0557x36). Reassuringly, this is not that dissimilar to our original estimate of 2.4 mm, thus demonstrating two important points. Firstly, that the result is robust and consistent. Secondly, that our original back-of-the-envelope approximation, much loved by physicists everywhere, did not let us down.

The advantage of calculating the fractional change in n using Eq. 15.6 rather than calculating ∆n directly is that it means that we can avoid the complication of working out the relative humidity. The Clausius-Clapeyron equation, strictly speaking, only applies to closed systems in equilibrium, i.e. at 100% relative humidity. In open systems, such as the Earth's atmosphere above large oceans, the humidity is always less than the maximum. But Eq. 15.6 effectively removes the issue of relative humidity as it just introduces an additional scaling term that applies more or less equally to n and ∆n. Therefore it cancels out in Eq. 15.6. All of this may be somewhat pedantic, however, as the sea level fall due to evaporation is a full two orders of magnitude less than the previous two effects considered.


So the conclusion is this: prophesies of apocalyptic rising sea levels and submerging cities are still just alarmist nonsense. The physics proves that there is currently not enough energy available to achieve this on the timescale that some climate scientists predict, at least not yet. Thermal expansion and melting ice caps will each add not much more than 2 mm per year to sea levels. A recent paper by Anny Cazenave et al. (Advances in Space Research 62(7) 1639-1653 (2018) ) puts the sea level rise (SLR) from all sources at about 3.5 mm per year for the period 2005-2015  (see Fig. 15.4 below). These numbers do appear to be more consistent with the surface energy imbalance of 0.9 W/m² reported by Trenberth and co-workers rather than the 0.6 W/m² of Stephens et al., particularly the thermal expansion component.

Fig. 15.4: Possible breakdown of different contributions to sea level rise (1993-2015) from Cazenave et al.

One of the striking features of Fig. 15.4 in my view is the low contribution to sea level rise from ice melt in Antarctica compared to that from glaciers. Three explanations spring to mind. Firstly, there is probably more warming in the Northern Hemisphere because that is where the heat is being generated. Secondly, the glaciers in Europe are very close to the source of that heating. And thirdly, the ice in Antarctica is much colder than that in alpine glaciers, and so requires more heat to melt it. So, as I pointed out in the last post, this could mean that alpine glaciers will continue to recede, not because of CO₂ emissions, but because of local human industrial activity that leads to surface heating of the local environment, and thus a temperature rise of more than 0.3 °C above pre-industrial levels.

14. Surface heating

The principal claim made by climate scientists is that global temperatures have increased by about 1 °C over the last 100 years. In the last post I outlined three ways that this might happen. The first, which was due to changes in the amount of solar radiation reaching the Earth, I discounted due to a lack of evidence or plausible mechanism. The last, changes to the radiative forcing term I will discuss at a later date. In this post I will consider the second possibility: changes to the amount of direct heat absorption at the surface of the Earth. There are essentially only two ways this can happen: (i) through changes to the Earth’s reflectivity or albedo; (ii) by direct heating of the surface from energy sources other than the Sun.

(i) Changing the Earth’s albedo.

As I explained in the last post, one way that the Earth's surface temperature might change is if the proportion of light from the Sun that is reflected from the surface were to change. The amount reflected is called the albedo. This effect can be seen in Fig. 14.1 below which is taken from a 2009 paper by Kevin Trenberth, John Fasullo and Jeffrey Kiehl (Bull. Amer. Meteor. Soc. 90 (3): 311–324). On the left of Fig. 14.1 where the direct radiation from the Sun (in yellow) impacts the surface, the radiation is partially reflected with 23 W/m² being reflected and 161 W/m² is absorbed. This equates to an albedo of 0.125 ( = 23/(23+161) ).

As an aside: it seems slightly suspicious that the fractions reflected at the surface (1/8) and at the top of the atmosphere (102/341 = 30%) are so close to simple fractions. Does this indicate a high degree of uncertainty in these numbers, I wonder?

Fig. 14.1: The Earth's energy balance according to Trenberth et al. (2009). 

In order for the surface temperature of the Earth to have increased by 1 °C, one way that this could have happened would be for the amount of energy absorbed at the surface to have increased over time by 2.3 W/m². If this were to be achieved through changes to the albedo, then the albedo would need to have decreased from 0.1375 to 0.125. That is a change of 0.0125. So how likely is this?

The albedo of the Earth's surface depends of the type of material of the surface, as shown in Table 14.1. It also depends on the angle of incidence of the light as light tends to reflect more off surfaces at glazing incidence. So ocean water at the equator has a lower albedo than it does near the poles. However, there is also much less surface area near the poles which consequently reduces the contribution of high angle reflectance. 

Surface	% of Earth's     Surface Area	Albedo    %	Contribution to the     Earth's Albedo
Ocean	71.00	6	0.0426
Forest	7.62	8-18	0.0091
Grassland	7.93	25	0.0198
Arable	2.37	17	0.0040
Desert sand	5.51	40	0.0220
Urban	0.21	20	0.0004
Glaciers & ice caps	2.90	80	0.0232
Shrub & tundra	2.46	15	0.0037

Table 14.1: Approximate albedo of different parts of the Earth's surface.

The most common claims made about land use and climate changes are in regard to deforestation, increasing agricultural use, and increased urbanization. First it is claimed that deforestation for farming, particularly livestock farming aids global warming. As far as changes to the albedo are concerned, the evidence in Table 14.1 seems to point the other way. Turning forests into grassland increases the albedo.

Urbanization is also generally believed to reduce albedo, partly through what is termed the urban heat island (UHI) effect. This is the theory that cities with large amounts of concrete soak up more heat, and tall buildings trap that heat. This may be true, but it may also be a small localized effect. Again the data in Table 14.1 does not support it as a major driver of global warming.

A third claim is often made about polar ice and glaciers. The claim is that, because ice and snow have high levels of albedo, any change in their total albedo would have a large impact on global temperatures. The two main negative effects cited tend to be reductions in area by melting, or black carbon soot particles that drop on the surface and reduce the albedo. The main problem here is that the changes required are huge; a 54% decrease in area, or a decrease in albedo from 0.80 to 0.37. The first obviously has not and will not happen, and the latter is very unlikely as it would require huge levels of soot deposits.

The conclusion is, therefore, that changes to the Earth's albedo are difficult to achieve, and any that might have occurred have probably produced very little real effect in terms of increasing global temperatures.



(ii) Direct anthropogenic surface heating due to human and industrial activity.

The proposition here is this. All energy generation by humans results in an output of heat or thermal energy. Not only does every industrial process produce waste heat, but all mechanical work that is done by that process eventually ends up as heat or entropy as well. These are the consequences of the Second Law of Thermodynamics, and as every physicist knows, nothing can defeat the Second Law of Thermodynamics. So as temperature is just a measure of heat and entropy, it follows that everything humans do, every industrial process they create, all the energy that goes in will, in the end, just heat up the environment.

In the last post I showed that an increase of 2.3 ± 0.5 W/m² in the amount of radiation at the surface would raise global temperatures by 1 °C. So if we can work out what the rate of energy production and consumption by humans is, then we can equate that to a global temperature rise. The starting point for this is clear: we know from IPCC reports and the protestations of climate scientists that the human race currently emits 36 gigatonnes of carbon dioxide (CO₂) into the atmosphere. That CO₂ is created primarily by three processes.

The first is the burning of pure carbon (from coal) that produces an energy output of 394 kJ/mol for the process

(14.1)

The second is burning of methane (natural gas) that produces an energy output of 882 kJ/mol for the process

(14.2)

The third is the burning of higher alkanes (from oil) that produces an energy output of about 660 kJ per mole of CO₂ for the process

(14.3)

Each of the above energy outputs is for the burning of carbon or hydrocarbons to produce one mole of CO₂. To work out how energy that amounts to in total we need to know how much of each type of fossil fuel was used.

In 2018 global coal production was 7665 million tonnes, natural gas production was 3955 billion cubic metres or 2786 million tonnes (assuming 1 cubic metre = 704.5 g), and crude oil production was 4472 million tonnes. That suggests a mean energy output of about 560 kJ/mol. As 36 gigatonnes of carbon dioxide equates to 8.18 x 10m¹⁴ moles, then the total energy consumption would have been 4.58 x 10²⁰ J for the year, or 52,268 TWh.

Fig. 14.2: Global fossil fuel consumption since 1800.

However, according to the Our World In Data website, the global energy consumption from fossil fuels in 2017 amounted to 36,704 TWh from natural gas, 53,752 TWh from crude oil and 43,397 TWh from coal (see Fig. 14.2 above). The total of these values (133,853 TWh) is 2.53 times the value based on CO₂ emissions and suggests only 39% of fossil fuel combustion results in CO₂. This higher figure equates to an average power density at the Earth's surface of 0.030 W/m² across the whole surface of the Earth. That is turn implies a global temperature increase (based on the 2.3 W/m² required for a 1 °C increase that I demonstrated in the last post) of 0.013 °C compared to pre-industrial times. This, though, still omits the impact of nuclear power and renewables.

Fig. 14.3: Global energy production by energy type (2005-2018).

According to Statistica.com renewables and nuclear energy accounted for 15.3% of global energy consumption in 2018, and fossil fuel usage in 2018 exceeded that in 2017 (see Fig. 14.3 above), so that implies a global temperature increase of at least 0.015 °C compared to pre-industrial times. This temperature increase of 0.015 °C is, however, at least 60 times less than the one the IPCC is claiming for global warming since 1850. So this suggests that any resulting surface heating is such a small effect that we can safely ignore it, right? Well, not so fast.

We know that this heat is not spread evenly, its impact is greatest in the areas where most people live and work. We know that 90% of people live in the Northern Hemisphere; we know that 99.999% of people live on land. It is also true that 90% of weather stations are in the Northern Hemisphere, and at least 99.9% of them are on land. In other words there is a high degree of correlation between where people live, where industrial energy usage is, and where the weather stations are. For example, 19.7% of the Earth's surface is land in the Northern Hemisphere. So if 90% of the energy use is found there then the mean temperature rise on land in the Northern Hemisphere will be 0.069 °C. But of course, even that fails to tell the whole story. If we look at individual countries the results become even more stark.

If we start with what has been, historically, the biggest CO₂ producer, the USA, we see that it accounts for about 20% of global energy use despite being home to only 4.3% of the world's population, and covering only 1.6% of the Earth's surface area. That suggests that the power density for surface heating in the USA should be about 0.38 W/m² (an increase by a factor of 12.6 on the global average of 0.03 W/m²). This picture is confirmed by data from the US Energy Information Administration that indicates that the total power consumption of the 48 contiguous states (excluding Hawaii and Alaska) is 100.3 x 10¹⁵ BTU (see Fig. 14.4 below) over an area of 8.08 x 10⁶ km². As 1 BTU (British thermal unit) is the equivalent of 1055 J, this gives a power density for surface heating of 0.42 W/m². Yet this increases to 0.69 W/m² in Texas and 1.11 W/m² in Pennsylvania. That means that the temperature rise in Pennsylvania due to surface heating is almost 0.5 °C. But if we look at Europe the situation is even more extreme.

 Fig. 14.4: US energy consumption since 1950 by sector (in BTU).

According to the IEA, the UK's energy usage in 2018 was 177 million tonnes of oil equivalent (Mtoe), or 2059 TWh (1 Mtoe = 11.63 MWh). As the area of the UK is only 242,495 km², that equates to a power density of 0.97 W/m² and a temperature rise of 0.42 °C. But it is safe to assume that that energy usage will not be spread evenly across the country. At least 84% of both the UK population and UK economic activity is found in England (with an area of 130,395 km²) which implies a temperature rise for England alone of 0.66 °C. Yet that is still modest compared to Belgium and the Netherlands with their much higher population densities (see Table 14.2 below) where the projected temperature rise is close to 1.0 °C. That is more than the IPCC claims for global warming from greenhouse gas emissions.

Country	Energy Usage (Mtoe)	Power Density (W/m2)	Temperature Rise (°C)
UK	177	0.97	0.42
Italy	151	0.66	0.29
France	245	0.50	0.22
Belgium	52	2.25	0.98
Netherlands	72	2.30	1.00
Germany	298	1.11	0.48
Austria	33	0.52	0.23
Switzerland	24	0.77	0.34

Table 14.2: Energy usage, surface heating and temperature rise in Europe.

What Table 14.2 illustrates is that surface heating is a significant factor in overall global warming, and it is occurring in every major EU country, including those that border the Alps. In fact the average temperature rise over all five of the main alpine countries is 0.30 °C. It is perhaps no wonder then that the alpine glaciers have been retreating for over a century, while those in Norway and New Zealand, where the population density (and also the economic activity) is much lower, have remained more stable. But what this warming is not due to is increased CO₂ levels in the atmosphere or an enhanced Greenhouse Effect. That is a completely separate issue.

The conclusion we can draw from this is that, in most developed countries, warming of up to 1.0 °C has occurred since pre-industrial times, and this warming is solely a result of industrial activity and the heat that is generated as a result of that activity. This will occur irrespective of the energy type or source used because it is the heat that is directly warming the planet, not increases in the concentration of waste gases that then add to the Greenhouse Effect. This also means that when the energy usage goes down, the temperature should go down.

This has major implications for future energy policy because it means that nuclear power and most renewables are no better than fossil fuels. It also means that the efficiency of energy generation is as important as the quantity of energy generation in determining the amount of warming.

Fig. 14.5: Efficiencies of different power sources.

As an example of the impact of energy efficiency consider the case of solar photovoltaics. The relative efficiencies of different power sources are illustrated in Fig. 14.5 above. Of these photovoltaics are among the least efficient. They are in fact only about 15% efficient, meaning that for every 100 joules of energy they harvest from the Sun, they only create 15 joules of electricity. Yet in order to do this solar cells need to be 95% efficient in terms of absorbing incoming solar radiation. In other words their albedo needs to be less than 0.05. That means that for every 100 joules of solar radiation that falls on a solar cell, 5 joules is reflected back into space, 15 joules is turned into electricity (which will then become surface heat at the point of use), and 80 joules becomes waste surface heat in the solar cell.

Now a fashionable policy proposal at the moment is to put large numbers of photovoltaics in the Sahara Desert and then pump the electricity they produce to wherever it is needed. The problem is that not only will the electricity generated heat the location of its end user, but the solar cells will heat up the desert by decreasing the local albedo from 0.40 to 0.05. That is a double whammy. It is global warming without the need for CO₂. Now you don't hear much about that from climate scientists.

13. The Earth's energy budget

In order to understand how the Earth is heating up, you need to understand why it is warm in the first place. That means you need to know where the energy is coming from and where it is going. That is the basis of the Earth's energy budget or energy balance.

The purpose of this post is to analyse that energy balance, and to determine which parts of it can change, and what the effects of those changes are likely to be. Specifically, this post will try to relate various possible changes in the energy balance to any consequential changes in global temperatures. In so doing, it will also be necessary to critically ascertain the degree of confidence that there is surrounding the various estimates, and measurements, regarding the energy flows in the different parts of the atmosphere.

As I pointed out in the last post, virtually all the energy that is present on Earth originated in the Sun. The amount of energy per second arriving from the Sun at the top of the Earth’s atmosphere is 1361 watts per square metre (W/m²), and as I also pointed out, because the area this energy is ultimately required to heat up (4πr² where r is the Earth's radius) is four times the cross-sectional area that actually captures the energy (πr²), that means that the mean power density (remember: power is rate of flow of energy) that the Earth receives is only a quarter of the incoming 1361 W/m², or about 341 W/m². However as I also showed in Fig. 12.1, not all this energy reaches the Earth's surface. In fact only about 161 W/m² does. The rest is either absorbed by the atmosphere (78 W/m²), reflected by the atmosphere and clouds (79 W/m²), or is reflected by the Earth's surface (23 W/m²). This is shown diagrammatically in Fig. 13.1 below.

  

Fig. 13.1: The Earth's energy budget as postulated by Trenberth et al. (2009).

The image in Fig. 13.1 is taken from a 2009 paper by Kevin Trenberth, John Fasullo and Jeffrey Kiehl (Bull. Amer. Meteor. Soc. 90 (3): 311–324). It is not necessarily the most definitive representation of the energy flows (as we shall see there are other models and significant disparaties and uncertainties in the numbers), but it is probably the most cited. The data it quotes specifically relates to the energy budget for the period March 2000 - May 2004.

Fig. 13.2: The Earth's energy budget as postulated by Kiehl and Trenberth (1997).

The 2009 Trenberth paper is not the first or last paper he has produced on the subject. The energy budget it describes is actually a revision of an earlier attempt from 1997 (J. T. Kiehl and K. E. Trenberth, Bull. Amer. Meteor. Soc., 78, 197–208) shown in Fig 13.2 above, and has since been revised again in 2012 (K. E. Trenberth and J. T.  Fasullo, Surv. Geophys. 33, 413–426) as shown in Fig. 13.3 below.

Fig. 13.3: The Earth's energy budget as postulated by Trenberth and Fasullo (2012).

The only real difference between the energy budget in Fig. 13.3 and that from 2009 in Fig. 13.1 is the magnitude of the atmospheric window for long wave infra-red radiation (revised down from 40 W/m² to 22 W/m²), but I still think this highlights the level of uncertainty that there is regarding these numbers. This is further emphasised by a contemporary paper from Stephens et al. (Nature Geoscience 5, 691–696 (2012) ) shown below in Fig. 13.4.

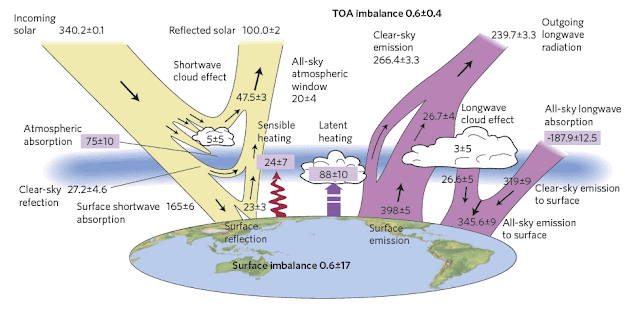
Fig. 13.4: The Earth's energy budget as postulated by Graeme L. Stephens et al. (2012).

As the 2009 Trenberth paper appears to be the most cited it is probably best to use this as the basis for the following discussion, but to bear in mind the amount of uncertainty regarding the actual numbers.

In Fig. 13.1 the three most significant numbers are those for the direct surface absorption from the Sun (161 W/m²), the upward surface radiation (396 W/m²), and the long-wave infra-red back radiation due to the Greenhouse Effect (333 W/m²). Of these it is the upward surface radiation (396 W/m²) that determines the temperature but its value is set by the other two.

As I explained in the last post the emission of electromagnetic radiation from a hot object is governed by the Stefan-Boltzmann law as shown below

  

(13.1)

where I(T) is the power density (per unit area) of the emitted radiation, σ = 5.67 x 10^-8 Wm^-2K^-4 is the Stefan-Boltzmann constant, and the term ε is the relative emissivity of the object. The emissivity defines the proportion of the emission from that object at that wavelength compared to a black body at the same temperature, and it varies with wavelength. It is also different for different materials. In the case of planet Earth, it is generally assumed to be very close to unity all over the surface for all emission wavelengths, but this is not always the case.

It is Eq. 13.1 that allows us to determine the surface temperature (T = 289 K) from the upward surface radiation (396 W/m²) or visa versa. It also allows us to calculate the change in upward surface radiation that would result from a given increase in the surface temperature. It turns out that an increase in surface temperature of 1 °C would necessitate the upward surface radiation increasing from 396 W/m² to 401 W/m², in other words a 1.39% increase. A 2 °C increase would require a 2.80% increase in the upward surface radiation.

I also explained in the last post how the total upward surface radiation (I_T) was related to the direct surface absorption from the Sun (I_o) via a feedback factor f which represented the fraction of upward surface radiation that was reflected back via the Greenhouse Effect.

(13.2)

This model assumed that all the energy absorbed by the greenhouse gases came from one source, though, namely surface upward radiation, and was driven by a single input, the surface absorption of solar radiation, I_o. As Fig. 13.1 indicates, this is not the case. This means that Eq. 13.2 will need to be modified.

The aim here is to determine what changes to the energy flows in Fig. 13.1 would result in a particular temperature rise, specifically a rise of 1 °C in the surface temperature. Realistically, there are only three things that could bring about any significant change. The first is a change in the amount of energy coming from the Sun. The second is is a change in the direct absorption of radiation at the surface, I_o. The third is a change in the strength of the Greenhouse Effect, f.


Case 1: Changes to the incoming solar radiation.

This is probably the easiest of the three propositions to analyse. If the incoming solar radiation at the top of the atmosphere were to change by 1.39%, then we would expect virtually all the projected heat flows in Fig. 13.1 to change by the same amount, including the upward surface radiation (from 396 W/m² to 401 W/m²). This is because almost all the scattering mechanisms and absorption processes in Fig. 13.1 are linear and proportional. The two exceptions are likely to be the thermals (17 W/m²) and the evapo-transpiration (80 W/m²), the former of which will be governed more by temperature differences, and the latter by the non-linear Clausius-Clapeyron equation. While changes to these two components are likely to be linear for small changes, they are unlikely to be proportional. However, as the changes to these two components are likely to be fairly small and comparable to other errors, we can probably ignore these deficiencies. So, if the incoming solar radiation (1361 W/m²) were to increase by 1.39% we could see a global temperature rise of 1 °C.

The problem is that there is no evidence to suggest the Sun's solar output has changed by anything like 1.39% over the last 100 years, and no obvious theoretical mechanism to suggest that it could. The only evidence of change is from satellite measurements over the last 40 years or so that suggest an oscillation in solar output with an eleven year period and an amplitude of about 0.05% (see Fig. 13.5 below). This would give a maximum temperature change of about 0.1 °C.

Fig. 13.5: Changes in the Sun's output since 1979 (from NOAA).

The only other known mechanism is the Milankovitch cycle. This can produce temperature oscillations of over 10 °C in magnitude (peak to trough) but is only seen over 120,000 year cycles (see red curve in Fig. 13.6 below). 

Fig. 13.6: Changes to temperature in the southern oceans (red curve) derived from isotope analysis of the Vostok ice core in Antarctica.

These temperature oscillations are mainly due to changes in the Earth's orbit around the Sun (changes to a more elliptical ortbit), or changes in the Earth's angle of inclination or tilt, or an increased precession that then exposes the polar regions to higher levels of solar radiation. Such effects may be responsible for the cycle of ice ages, but cannot be responsible for changes thought to have happened over the last 100 years. As the data in Fig. 13.6 indicates, even the periods of fastest climate change amounted to only a 10 °C increase over 10,000 years, or 0.1 °C per century, and we do not appear to be in one of those warming periods. If anything, the planet should be slowly cooling by about 0.01 °C per century.

The conclusion, therefore, is that global temperatures may fluctuate by 0.1 °C across the decade due to changes in solar output, but there is no evidence or credible mechanism that would support a long-term warming trend.


Case 2: Changes to the direct absorption of radiation at the surface.

The second possible driver of global warming comes from changes at the surface, specifically to the thermal energy absorbed there, I_o. This will then impact on the total upward surface radiation I_T and thereby also on the back radiation. According to Eq. 13.2 the changes to I_o and I_T should be proportional. As Eq. 13.1 indicates that a 1 °C change to the surface temperature, T_o, should result in a 1.39% change to I_T, it follows that a 1.39% change to I_o should result in a 1 °C change to T_o. Unfortunately there are three additional complications that we need to consider: the thermals (I_th = 17 W/m²), the evapo-transpiration (I_E = 80 W/m²), and the incoming solar radiation absorbed by the atmosphere (I_A = 78 W/m²).

The thermals (17 W/m²) and evapo-transpiration (80 W/m²) in Fig. 13.1 transfer heat from the surface into the upper atmosphere (top of the tropopause) by mass transfer (convection) rather than radiation. This may potentially provide a route for heat to escape from the Earth via a by-passing of the greenhouse mechanism. However, I would expect this energy to eventually get dumped in the atmosphere somewhere before the top of the tropopause (at a height of 20 km). When this happens it will merely add to the long-wave infra-red radiation being emitted from the surface, and so should still be reflected by the greenhouse gases. So while these heat sources will not contribute to the surface temperature as defined in Eq. 13.1, they should be included in the feedback factor f in Eq. 13.2.

So too will some of the power absorbed by the atmosphere directly from the incoming solar radiation (78 W/m²). Here again things are complicated because if the energy is absorbed before the bottom of the stratosphere (at 20 km altitude), the Greenhouse Effect will actually reflect some of that heat back into space. To account for this we can include an additional parameter μ as a variable that specifies the proportion of the incoming solar absorbed by the atmosphere that is absorbed in the lower atmosphere where it can be reflected backwards the surface. The fraction (1-μ) absorbed in the upper atmosphere will escape and therefore will not contribute to the back radiation.

In all there are seven energy terms that we need to consider.

1. Initial surface absorption (I_o = 161 W/m²).
2. Thermals (I_th = 17 W/m²).
3. Evapo-transpiration (I_E = 80 W/m²).
4. Upward surface long-wavelength radiation (I_up = 396 W/m²).
5. Long-wavelength back radiation (I_RF = 333 W/m²).
6. Incoming solar absorbed by the atmosphere (I_A = 78 W/m²).
7. Net radiation permanently absorbed by the Earth's surface (I_net = 0.9 W/m²).

We must then consider energy conservation at the surface and in the atmosphere. At the surface the law of conservation of energy (1st law of thermodynamics) requires that

 (13.3)

while in the atmosphere similar considerations mean that the total energy entering the atmosphere must equal the total that is emitted. As f is the proportion that is reflected back it follows that

(13.4)

The parameter μ is a variable that specifies the proportion of the incoming solar absorbed by the atmosphere (I_A) that is absorbed in the lower atmosphere where it can be reflected back towards the surface. The fraction (1-μ) absorbed in the upper atmosphere will escape and therefore will not contribute to I_RF. It therefore follows that

(13.5)

Using Eq. 13.5 we can work out a value for f, but only if we know μ, which we don't. However, using Eq. 13.4 and the knowlege that μ must lie in the range 0 <  μ < 1, we can say that f will be in the range 0.583 to 0.675 and that when μ = 0.5, f = 0.626. This allows us to estimate the change required in I_o to generate a 1 °C change in T_o, but to do that we will need to make some assumptions given the number of variables that there are.

First we can probably assume that f, μ and I_A remain unchanged even when I_o changes. We know that a 1 °C increase in T_o will result in a 1.39% increase in I_up to 401.5 W/m² and a 2 °C increase in T_o will result in a 2.80% increase in I_up to 407.1 W/m². The question is what happens to the thermals (I_th), the evapo-transpiration (I_E) and the net surface absorption (I_net)? They will probably increase as well, but by how much? A good starting point is to assume that they will increase by the same percentage as the upward surface long-wavelength radiation (I_up). A benchmark control is to assume that they stay constant. This gives us the following two scenarios.

If I_th, I_E and I_net scale with I_up and the scaling factor due to the increase in temperature T_o is g, then Eq. 13.5 can be rearranged to give

(13.6)

whereas if I_th, I_E and I_net are constant then

(13.7)

We know that g = 1.0139 for a 1 °C rise in T_o and g = 1.0280 for a 2 °C rise in T_o. So combining the two options in Eq. 13.56 and Eq. 13.7 implies that I_o is in the range 162.8-163.9 W/m². That implies an excess direct heating at the surface of ∆I_o = 2.33 ± 0.54 W/m², with the error range being set by the range of possible values for f, μ, I_E, I_net and I_th. A 2 °C increase in surface temperature would require a change in direct heating at the surface of ∆I_o = 4.69 ± 1.09 W/m².

The conclusion, therefore, is that a 1 °C increase in global temperatures would require an increase in the initial surface absorption of ∆I_o = 2.3 ± 0.5 W/m². How this might be achieved will be explored further in the next post.


Case 3: Changes to the feedback factor.

The most obvious and heavily reported mechanism by which global temperatures could increase is via changes to the Greenhouse Effect due to increased carbon dioxide concentrations in the atmosphere. The specific change that will ensue will be in the value of the feedback term, f, and hence the value of the back radiation, I_RF. As in the previous case, some of the heat flow parameters in Fig. 13.1 would change and some would stay the same. For example, we can confidently assume that I_A and I_o will remain unchanged, but if f changes, so might μ. But as before, the main question is what happens to the thermals (I_th) and the evapo-transpiration (I_E)?

Rearranging Eq. 13.5 once more gives

 (13.8)

while for the case that I_th, I_E and I_net are constant we get

 (13.9)

It turns out there is very little difference in the results using the two methods. The biggest factor affecting f is the value of μ. When there is no warming (g = 1.0) f = 0.629. A warming of 1 °C (g = 1.0139) requires f to increase to 0.634, and a warming of 2 °C (g = 1.0280) requires f to increase to 0.638. These values all correspond to values for μ of 0.5, but the possible spread of values for μ leads to an error in f of ±0.047 in all cases.

What this shows is that the increase in feedback factor needed for a 1 °C rise in global temperatures will be about 0.005. This is a small change, but at the end of the last post (Post 12) I calculated that the fraction of the long-wave infra-red radiation that could be absorbed and reflected by the carbon dioxide in its main absorption band (the frequency range 620-720 wavenumbers or the wavelength range 13.89 - 16.13 μm). The result was at best 10.5%. This implies that only about 15% of the Greenhouse Effect is due to CO₂, and the rest is due to other agents, mainly water vapour.

The conclusion, therefore, is that a 1 °C increase in global temperatures would require an increase in the width or strength of the carbon dioxide absorption band by at least 5% relative to its current size in order achieve this temperature rise.


The final point to note is the size of the potential measurement errors in the various energy flows, and the effect of rounding errors. A particular egregious anomaly occurs at the top of the atmosphere in Fig. 13.1 (and remains uncorrected in Fig. 13.3) where the rounded value of the incoming solar (341 W/m²) radiation balances the rounded outgoing values (239 W/m² and 102 W/m²). This is inconsistent with the rest of the diagram as there should be a 0.9 W/m² difference to account for the net absorption at the surface. In the more exact values quoted (341.3 W/m², 238.5 W/m² and 101.9 W/m²) this difference is specified correctly. So the problem is a rounding issue initially, but it then has a knock-on effect for the values quoted within the atmosphere.

For consistency it would therefore be better in this instance to round the 238.5 W/m² value down (to 238 W/m²) rather than up (to 239 W/m²). That would ensure that there was a net inflow of about 1 W/m² that balanced the net absorbed value at the surface (0.9 W/m²). It would also eliminate the false imbalance within the atmosphere itself. Here the net inflow should balance the net outflow (currently there is a 1 W/m² deficit). There can be no 0.9 W/m² energy gain in the atmosphere otherwise the atmosphere would heat up, and heat up by more than 2.7 °C per annum. What should remain invariant at various points from the surface to the top of the atmosphere is the following energy balance

(13.10)

where I_TOA = 238.5 W/m² is the outgoing long-wave radiation at the top of the atmosphere. A correction for this error requires the stated value for the power emitted upwards by the atmosphere (169 W/m²) in Fig. 13.1 to be reduced to 168 W/m².

It is also important to note that some of the errors in the energy flows in Fig. 13.1-Fig.13.4 are considerable, either in magnitude, or as a percentage. A comparison of the data in Fig. 13.1 and Fig. 13.4 illustrates how variable the results can be. The back radiation values, for example, do not agree within the noted error range, and the net surface absorption is 50% higher in Trenberth's papers than it is in the Stephens paper (Fig. 13.4). I shall look at the net surface absorption in more detail later as it has important implications for sea level rise, but the fact that this value is so small, not just relative to the other energy flows, but also in comparison to their errors, is a cause for concern with respect to its own accuracy. It should also be noted that the net surface absorption should also be measurable directly at the top of the atmosphere using satellite technology to measure both the solar energy going in and the Earth's thermal energy flowing out. Yet the discrepancies seen there between incoming and outgoing energy flows currently far exceed 0.9 W/m². The result is that most of the energy flows shown in Fig. 13.1-Fig.13.4 are at best estimates, and are often based more on climate models than on actual data.

12. Black body radiation and Planck's law

Before you can understand how the Earth is heating up, you need to understand why it is warm in the first place. That means you need to appreciate the basic physics. Central to an understanding of how the Earth's surface temperature comes about are two important laws of physics: Planck's law and the Stefan-Boltzmann law. Both these laws describe in different ways how electromagnetic radiation is emitted from what in physics is termed a black body. Together they explain why the Earth's surface temperature is as it is.

Almost all the Earth's energy (other than a bit of geothermal energy, some naturally occurring nuclear decay, and a few cosmic rays) comes from the Sun. The Sun is predominantly a ball of fiery hydrogen plasma with a surface temperature of about 5505 °C (or 5778 K). The energy it produces comes from the nuclear fusion of that hydrogen into helium within its core (the core being defined as the region of the interior that is less than 0.7R_s from the centre, where R_s is the distance from the centre of the Sun to its outer edge). This fusion process gives off electromagnetic radiation with a range of frequencies, but which are mainly in the visible portion of the electromagnetic spectrum. It is the force of this radiation pushing out as it tries to escape that stops the Sun collapsing into a black hole under its own gravitational force. It also takes up to a year for many of these photons (particles) of light to actually escape. By contrast it only takes a further 8 minutes and 24 seconds for them to reach Earth.

The energy released by the Sun is 3.9 x 10²⁶ joules per second, or a power of P = 3.9 x 10²⁶ W. This is dispersed uniformly in all directions so that by the time it reaches Earth (at a distance r = 1.519 x 10¹¹ m from the Sun), it has spread out (due the inverse-square law) over a sphere in space of area A = 2.9 x 10²³ m² (= 4πr²). This means that the intensity of the radiation that we receive is P/A, or 1361 W/m². This is the power per unit area reaching Earth at the top of its atmosphere, and it still comprises the full range of different frequencies that were emitted from the Sun, each with a different relative intensity, as illustrated below in Fig. 12.1.

Fig. 12.1: The electromagnetic radiation output of the Sun (yellow) and the radiation received at ground-level on Earth (red).

What Fig. 12.1 shows is that the Sun's radiation output closely (but not exactly) resembles that from a black body of temperature 5250 °C (black curve), and that not all this radiation arrives at ground-level on Earth. Some is blocked by the atmosphere and reflected back into space.

In physics a black body is defined as an object that absorbs all the electromagnetic radiation that falls on its surface. It also has the property that when it is in thermal equilibrium with its surroundings at a constant thermodynamic temperature (i.e. the temperature measured on the kelvin scale), then it will emit heat in the form of electromagnetic radiation across a continuous range of frequencies. The distribution or spectrum of those frequencies is known as the black body spectrum, and it always has the normalized functional form shown in Fig. 12.2 below.

Fig. 12.2: The black body frequency spectrum.

The curve in Fig. 12.2 is described by the general equation

(12.1)

where a = 15/π⁴ is a scaling constant that ensures that the area under the curve is 1, and the parameter x depends on the thermodynamic temperature T (in kelvin) and the electromagnetic frequency (ν) as follows:

(12.2)

The other terms are Planck's constant, h, and the Boltzmann constant, k. By using the normalized variable x in Eq. 12.1 instead of ν and T, the equation can be applied universally. It is also worth noting that as λν = c, where λ is the wavelength of the radiation and c is the speed of light, it follows that x = b/Tλ where b = 14387.9 µm.K.

The actual intensity of the radiation emitted by a black body is then given by Planck's law as follows

(12.3)

where B(ν,T) represents the power per unit area of the surface emitted per steradian of solid angle. The total power emitted by a unit area of the surface, I(T), is therefore the sum of B(ν,T) over all frequencies and solid angles (this adds a factor of 2π for the half sphere the emission is flowing into).

(12.4)

We have already defined in Eq. 12.1 that

(12.5)

so it follows that

(12.6)

The result is known as the Stefan-Boltzmann law and σ = 5.67 x 10^-8 Wm^-2K^-4 is the Stefan-Boltzmann constant. This law represents the power that will be emitted from a perfect black body at a temperature T. This therefore represents the maximum power that any real object at that temperature can emit. In reality the emission is always less because no object behaves like a perfect black body, except a black hole.

What this demonstrates is that the power density output of a black body is not only proportional to the fourth power of the temperature, but it depends only on temperature. All the other quantities in σ are fundamental constants that cannot be changed. From this law we can therefore work out the maximum power output of the Sun. The surface temperature is 5778 K, so from Eq. 12.6 the power density of the emitted radiation is 63.2 MW/m². As the radius of the Sun is about 700,000 km, the surface area is 6.16 x 10¹⁸ m². So the total power output is 3.9 x 10²⁶ W, in agreement with the value at the top of this post.

Using these same equations we can now work out how hot the Earth will become when illuminated by the Sun's rays. We have already determined that the radiation intensity at the top of the atmosphere is I_TOA = 1361 W/m². The amount of power captured by the Earth will therefore be I_TOA multiplied by the cross-sectional area of the Earth πR_E² where R_E is the Earth's radius. But, as the Earth spins on its axis, this energy will need to heat up the entire surface area of the sphere, i.e. an area of 4πR_E². So the mean power density striking the Earth's surface will be a quarter of 1361 W/m², or 340.25 W/m².

This power will heat up the surface of the Earth until the point is reached where the temperature of the surface is high enough to ensure that the power that the Earth re-emits through the Stefan-Boltzmann law balances the incoming power from the Sun. This will happen when the surface temperature T_s is high enough so that σT_s⁴ = 340.25 W/m². This equates to a temperature of T_s = 278 K or 5 °C. This is not the mean temperature of planet Earth, though. It is what the mean temperature would be if the Earth had no atmosphere and the surface were completely absorbant and black. Except that this neglects the effects of the curvature of the Earth and its thermal conductivity. The former would mean the temperature at the poles would barely rise above 3 K (-270 °C), and that at the equator it could be as high as 393K or 120 °C in the daytime. The thermal conductivity of the surface would, on the other hand, mitigate these extremes.

In reality much of the incoming radiation is reflected by the atmosphere, the clouds, and the surface. This is the origin of the difference in the red and yellow areas in Fig. 12.1. The net result is that only about 161 W/m² gets absorbed by the Earth's surface, so according to Eq. 12.6 the surface temperature should not rise above 231 K, or -42 °C. However, this isn't true either. The mean temperature is actually closer to 289 K, or +16 °C. This is where the Greenhouse Effect comes into play.

While the atmosphere stops much of the incoming radiation getting in, it also stops much of the longer wavelength radiation emitted by the surface (and acting as a black body at 231K) getting out. Because the surface of the Earth is at a much lower temperature than the Sun, most of the radiation it emits will be at a much lower frequency, or longer wavelength. Some of this radiation then gets reflected back by the atmosphere, and in particular by the greenhouse gases, carbon dioxide and water vapour.

If the fraction reflected back we denote by f, and the reflected power is I_r, then it follows that I_r = f I_T, where I_T is the total power emitted from the surface. But as I_r is now incident on the Earth's surface, it too must be absorbed and add to the heating. It therefore follows that

(12.7)

where I_o = 161 W/m² is the original power absorbed by the Earth's surface. Following some elementary algebra we then obtain the result

(12.8)

As f is a number between 0 and 1.0, it follows that I_T will be greater than I_o. That in essence is the Greenhouse Effect with I_T being the power emitted from the Earth's surface with the Greenhouse Effect included, and I_o being the power emitted with it omitted. The only debate is what the value of f is, and by how much it is changing. Based on a surface temperature of 289 K, it would appear that f = 0.593; in other words 59.3% of the emitted power is reflected back. It is this value that I will look at in more detail next time when I discuss the Earth's energy budget.

On a final note, I will now go back to the emission spectra in Fig.12.1 and Fig. 12.2. There is an inconsistency here in that the first is a function of wavelength (λ), while the second (and most of the subsequent equations) is a function of frequency (ν). Does this matter? Well yes, particularly if you are wanting to calculate the total energy, or find the emission peak.

The peak or maximum of the curve in Fig. 12.2 occurs when x = 2.821, which means that for any object at a constant thermodynamic temperature, T, the frequency at which the maximum amount of radiation is emitted from that object, ν_max, is determined by the following formula:

(12.9)

For the Sun with a surface temperature of 5778 K, the peak frequency is 3.39 x 10¹⁴ Hz or 339 THz.

For those who may have forgotten their basic high-school physics, I remind you that frequency and wavelength are related by the equation λν = c, where c is the wave speed. For electromagnetic radiation c is the speed of light and it is always constant and the same for all wavelengths and frequencies. This means as the wavelength increases, the frequency decreases, and visa versa. It also means that as the speed of light is 3 x 10⁸ m/s, the frequency ν_max corresponds to a wavelength of 885 nm. Yet the peak in the solar spectrum in Fig. 12.1 is at 500 nm. So why are these two numbers not the same?

Well the crux of the problem is this. The theoretical black body spectrum in Fig. 12.2 with its peak at 2.821 in dimensionless units is a scaled version of Eq. 12.3. The quantity B(ν,T) represents the power density for each unit of frequency. When you integrate the area under the curve you get the total power. Now if you plot B(ν,T) as function of wavelength (λ) you are basically plotting the function below

(12.10)

For the case T = 5778 K this will still have a peak at λ = 885 nm, but when you integrate under this curve with respect to λ you do not get the result in Eq. 12.6. In other words, the area under this curve is not equal to the total power density. Instead you need to integrate with respect to the frequency and that means making the following transformation:

(12.11)

Note the switch of limits in Eq. 12.11 (zero to infinity and the reverse). The first switch occurs because the limits are now for λ and not ν. The second switch is because the differential of ν with respect to λ yields -c/λ² and removing the minus sign reverses the limits again. The result is that the equivalent spectral function for wavelength will be

(12.12)

If the function D(λ,T) is integrated over all wavelengths, the total power density is obtained.

(12.13)

Because the index of 1/λ in the function D(λ,T) is different from the index of ν in B(ν,T), it follows that the peaks in each spectra will be at different wavelengths because these are now inherently different equations. We can demonstrate this by defining a new dimensionless parameter y such that

(12.14)

where x is the same term as was introduced in Eq. 12.2. It then follows from Eq. 12.1, and using the differential result from Eq. 12.11, that we can define a second dimensionless term for λ that has the form

(12.15)

where again a = 15/π⁴. The area under this curve does indeed equal unity as before

(12.16)

which means that the function D(λ,T) can be rewritten to incorporate q(y) as follows:

(12.17)

If the function q(y) is plotted as a function of y, the result is the curve shown in Fig. 12.3 below.

Fig. 12.3: The black body wavelength spectrum.

The peak or maximum of the curve in Fig. 12.3 occurs when y = 0.201, which means that for any object at a constant thermodynamic temperature, T, the wavelength at which the maximum amount of radiation is emitted from that object, λ_max, is determined by the following formula:

(12.18)

This in turn leads to Wien's displacement law, which states that the product of the black body temperature, T, and the peak wavelength at that temperature, λ_max, is always equal to the same constant. In other words

(12.19)

The value of W_λ is 2.90 x 10^-3 Km. That means that when the temperature of the object is 5778 K, the peak wavelength will be 501 nm. This is why the peak of the solar spectrum in Fig. 12.1 is in the visible region of the spectrum corresponding to yellow light. Then, if the temperature decreases, so the peak wavelength will move to higher wavelengths as shown in Fig. 12.4 below.

Fig. 12.4: The black body wavelength spectrum at different temperatures.

However, it is not just the wavelength spectrum that obeys Wien's displacement law; the frequency spectrum does as well, it is just that the constant W_ν is different. Substituting c/λ_max for ν_max in Eq. 12.9 results in Eq. 12.20.

(12.20)

The value of W_ν is 5.11 x 10^-3 Km. This means that when the temperature of an object is 5778 K, the peak wavelength for its thermal emission will be at 884 nm. But while the position of the peak may change, what does not change is the amount of power found in a particular spectral range, even if that range appears at different places in Fig. 12.2 and Fig. 12.3.

For example, visible light is generally found between wavelengths of 400 nm and 800nm. In the case of the solar spectrum, the 400 nm radiation will have an equivalent x value of 6.236 according to Eq. 12.2 and a y value of 0.160 according to Eq. 12.14. For 800 nm radiation the values are x = 3.118 and y = 0.321. If the area under the curve in Fig. 12.2 between x = 3.118 and x = 6.236 is measured, it turns out to be 0.460 or 46.0% of the total area under the curve. If we do the same for the curve in Fig. 12.3 between y = 0.160 and y = 0.321 then we get the same result. Perhaps more interestingly, and relevant is, if you do the same for a 289 K spectrum for wavelengths between 13.89 μm and 16.13 μm you get an answer of 10.5%, but that is another story.