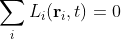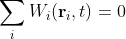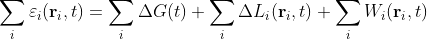9. Fooled by randomness

Is global warming real? That is probably a justifiable question given what I revealed in the last post about breakpoint alignment. But what I am going to demonstrate here and over the next two or three posts should also make you question everything you think you know about climate change. The first topic I am going to explore is a concept that most physicists and mathematicians are all too familiar with, but which appears to be totally off the radar of climate scientists: chaos theory and fractal geometry.

Fig. 9.1:  Record 1.

First a test. Look at the dataset above (Fig. 9.1) and the one below (Fig. 9.2). Can you tell which one is a real set of temperature data and which one is fake?

Fig. 9.2:  Record 2.

Okay, so actually it was a trick question because they are both real sets of data. In fact they are both from the same set of station data, and they are partially from the same time period as well, but there is clearly a difference. The difference is that the data in Fig. 9.1 above is only a small part of the actual temperature record but the data from Fig. 9.2 is from the entire record. The data in Fig. 9.1 is taken from the Christchurch station (Berkeley Earth ID - 157045) and is monthly data for the period 1974 - 1987. The data in Fig. 9.2 is from the same record but for the time interval 1864 - 2013: it has also been smoothed with a 12 month moving average. Yet they look the very similar in terms of the frequency and height of their fluctuations - why? Well, what you are seeing here is an example of self-similarity or fractal behaviour. The temperature record for Christchurch is a one-dimensional fractal, and so for that matter is every other temperature record.

Self-similarity is common in nature. You see it everywhere from fern leaves and cauliflowers to clouds and snowflakes. It is observed when you magnify some objects and look at them in greater detail, only to find, to your surprise, that the detail looks just like a smaller version of the original object. This is known as self-similarity: the object looks like itself but in microcosm. It is also an example of scaling behaviour. There is usually a fixed size ratio between the original and the smaller copies from which it is made.

In order to make the smoothed data in Fig. 9.2 look similar to the original data in Fig. 9.1 two scaling adjustments were made. First the time scale on the horizontal axis in Fig. 9.2 was shrunk by a factor of twelve. This is to compensate for the smoothing process which effectively combines twelve points into one. The second was to scale up the temperature axis in Fig. 9.2 by a factor 12 ^0.275. The reason for the power of 0.275 will become apparent shortly, but it is important as it has profound implications for the noise level we see in temperature records over long time periods (i.e. centuries).

To demonstrate the scaling behaviour of the temperature record we shall do the following. First we smooth the data with a moving average of length say two points and then calculate the standard deviation of the smoothed data. Then we repeat this for the original data, but with a different number of data points in the moving average and again calculate the standard deviation of the new smoothed data. After doing this for six or seven different moving averages we plot a graph of the logarithm of the standard deviation versus log(N) where N is the number of points used each time for the moving average. The result is shown below in Fig. 9.3.

Fig. 9.3:  Plot of the standard deviation of the smoothed  anomaly data against the smoothing interval N for temperature data from Christchurch (1864-2013).

The important feature of the graph in Fig. 9.3 is that the data lies on an almost perfect straight line of slope -0.275 (remember that number)? I have to confess that even I was shocked by how good the fitting was when I first saw it, particularly given how imperfect temperature data is supposed to be. What this graph is illustrating is that as we smooth the data by a factor N, the noise level is reducing by a factor N^-0.275. But is this reproducible for other data? Well the answer appears to be, yes.

Fig. 9.4:  Plot of the standard deviation of the smoothed  anomaly data against the smoothing interval N for temperature data from Auckland (1853-2013).

The graph above (Fig. 9.4) shows the same scaling behaviour for the station at Auckland (Berkeley Earth ID = 157062) while the one below (Fig. 9.5) illustrates it for the station at Wellington (Berkeley Earth ID = 18625). The gradients of the best fit lines (i.e. the power law index in each case) are -0.248 and -0.235 respectively. This suggests that the real value is probably about -0.25.

Fig. 9.5:  Plot of the standard deviation of the smoothed  anomaly data against the smoothing interval N for temperature data from Wellington (1863-2005).

But it is the implications of this that are profound. Because the data is such a perfect fit in all three cases, we can extrapolate to longer smoothing operations such as one hundred years. That corresponds to a scaling term of 1200 (because it is equal to 1200 months and thus is 1200 greater in period than the original data) and a noise reduction of 1200 ^0.25 = 5.89. In other words, the noise level on the underlying one hundred year moving average is expected to be about six times less than for the monthly data. This sounds like a lot but the monthly data for Christchurch has a noise range of up to 5 °C (see Fig. 9.6 below), so this implies that the noise range on a 100 year trend will still be almost 1 °C. Now if that doesn’t grab your attention, I have to wonder what will? Because it implies that the anthropogenic global warming (AGW) that climate scientists think they are measuring is probably all just low frequency noise resulting from the random fluctuations of a chaotic non-linear system.

Fig. 9.6:  The temperature anomaly data from Christchurch (1864-2013) plus a 5-year smoothing average.

What we are seeing here is a manifestation of the butterfly effect which, put simply, says that there is no immediate causal link between some current phenomena such as the temperature fluctuations we see today and current global events. This is because the fluctuations are actually the result of dynamic effects that played out long ago but which are only now becoming visible.

Fig. 9.7:  Typical mean station temperatures for each decade over time.

To illustrate the potential of this scaling behaviour further we can use it to make other predictions. Because the temperature record exhibits self-similarity on all timescales, it must do so for long timescales as well, such as centuries. So we can predict what the average temperature over hundreds of years might look like (qualitatively but not precisely) just by taking the monthly data in Fig. 9.6, expanding the time axis by a factor of 120 and shrinking the amplitude of the fluctuations by a factor of 120 ^0.25 = 3.310. The result is shown in Fig. 9.7 above. Because of the scaling by a factor of 120, each monthly data point in Fig. 9.6 becomes a decade in Fig. 9.7. The data in Fig. 9.7 thus indicates that the average temperature for each decade can typically fluctuate by about ±0.5 °C or more over the course of time.

Fig. 9.8:  Typical mean station temperatures over 100 years over time.

Then, if we smooth the data in Fig. 9.7, we can determine the typical fluctuations over even longer timescales. So, smoothing with a ten point moving average will yield the changes in mean temperature for 100 year intervals as shown in the graph above (Fig. 9.8). This again shows large fluctuations (up to 0.5 °C) over large time intervals. But what we are really interested in from a practical viewpoint is the range of possible fluctuations over 100 years as this corresponds to the timeframe most quoted by climate scientists.

To examine this we can subtract from the value at current time t the equivalent value from one hundred years previous, i.e. ∆T = T(t) - T(t-100).

Fig. 9.9:  Typical change in the 100-year mean temperature for a time difference of 100 years.

So, as an example we may wish to look at the change in mean temperature from different epochs, say from one century to the next. Well the data in Fig. 9.9 shows just that. Each data point represents difference between the mean temperature over a hundred years at that point in time with the same value for a hundred years previous. Despite the large averaging periods we still see significant temperature changes of ± 0.25 °C or more. However, if we compare decades in different centuries it is even more dramatic.

For example, Fig. 9.10 below predicts the range of changes in the average decadal temperatures from one century to the next, in other words, the difference between the 10-year mean temperature at a given time t and the equivalent decadal mean for a time one hundred years previous. What Fig. 9.10 indicates is that there is a high probability that the mean temperature in the 1990s could be 0.5 °C higher or lower that the mean temperature in the 1890s, and this is just as a consequence of low frequency noise.

Fig. 9.10:  Typical change in mean decadal temperature for a time difference of 100 years.

So why have climate scientists not realized all this? Maybe it's because their cadre comprise more geography graduates and marine biologists than people with PhDs in quantum physics. But perhaps it is also due to the unique behaviour of the noise power spectrum.

If the noise in the temperature record behaved like white noise it would have a power spectrum that is independent of frequency, ω. If we define P(ω) to be the total power in the noise below a frequency, ω, then the power spectrum is the differential of P(ω). For white noise this is expected to be constant across all frequencies up to a cutoff frequency ω_o.

(9.1)

This in turn means that P(ω) has the following linear form up to the cutoff frequency ω_o.

P(ω) = aω

(9.2)

where a is a constant. The cutoff frequency is the maximum frequency in the Fourier spectrum of the data and is set by the inverse of the temporal spacing of the data points. If the data points are closer together then the cutoff frequency will be higher. Graphically P(ω) looks like the plot shown below in Fig. 9.11, a continuous horizontal line up to the cutoff frequency ω_o.

Fig. 9.11: The frequency dependent power function P(ω) for white noise.

The effect of smoothing with a moving average of N points is to effectively reduce the cutoff frequency by a factor of N because you are merging N points into one. And because the noise power is proportional to the noise intensity, which is proportional to the square of the noise amplitude, this means that the noise amplitude (as well as the standard deviation of the noise) will reduce by a factor equal to √N when you smooth by a factor of N.

For a 100-year smoothing the scaling factor compared to a monthly average is 1200, and so the noise will therefore reduce by a factor of 1200 ^0.5 = 34.64 . That means the temperature fluctuations will be typically less than 0.1 °C. This is probably why climate scientists believe that the long term noise will always be smoothed or averaged out, and therefore why any features that remain in the temperature trend must be "real". The problem is, this does not appear to be true.

Instead the standard deviation varies as N ^-0.25. So the intensity of the noise varies as N ^-0.5 and P(ω) will increase as √N. It therefore follows that the power spectrum is not independent of frequency as is the case for white noise, but instead varies with frequency as

(9.3)

and P(ω) will look like the curve shown in Fig. 9.12 below.

Fig. 9.12:  The frequency dependent power function P(ω) for temperature data.

The net result is that the random fluctuations in temperature seen over timescales of 100 years or more are up to six times greater in magnitude than most climate scientists probably think they will be. So the clear conclusions is this: most of what you see in the smoothed and averaged temperature data is noise not systemic change (i.e. warming). Except, unfortunately, most people tend to see what they want to see.

8. New Zealand - trend due to long and medium stations

In the last post I looked at the long weather station records from New Zealand (i.e. those with over 1200 months of data) and showed how they could be combined to give a temperature trend for climate change using the theory outlined in Post 5. The result was a trend line that looked nothing like the ones Berkeley Earth and other climate science groups claim to have uncovered (compare Fig. 7.6 with Fig. 7.2 in Post 7).

Some may argue that part of the reason for this difference lies in the number of stations used (only ten), or the lack of data from the much larger group of seventeen medium length stations (with 401-1200 months of data each) that could have been utilized. To see if data from these stations does make a significant difference I have repeated the analysis process from the previous post, but with the seventeen medium length stations included alongside the original ten long stations.

The first problem we have, though, is that most of these medium stations have data that only stretches back in time to about 1960 and most of their data is post 1970. That means we cannot use the 1961-1990 period to determine the monthly reference temperatures (MRTs) that are needed to remove the seasonal variations (for an explanation of the MRT see Post 4). So instead I have chosen to use the period 1981-2000, which while not as long, is a period for which all 27 stations have at least 80% data coverage. After calculating the anomalies for each station, as before, the trend was determined by using the averaging method represented by Eq. 5.11 in Post 5. This gives the trend profile shown in Fig. 8.1 below.

Fig. 8.1: Average warming trend of for long and medium stations in New Zealand.

This trend is virtually identical to the one presented in the last post (see Fig. 7.6), which suggests that the additional data makes little difference to the slope, although there is a slight reduction in the noise level post-1970. The best fit line indicates a warming trend of only 0.27 ± 0.04 °C per century, again almost identical to that from the long stations alone (0.29 ± 0.04 °C per century). This also suggests that the choice of time period for the MRT has little effect as well. Yet if we look at the Berkeley Earth adjusted data we get a different picture.

Fig. 8.2: Average warming trend of for long and medium stations in New Zealand using Berkeley Earth adjusted data.

If we use Berkeley Earth adjusted data for both long and medium stations to determine the local warming trend for New Zealand we get the data in Fig. 8.2 above. The best fit line shows a significant +0.60 ± 0.04 °C per century upward slope.

Fig. 8.3: Smoothed warming trends of for long and medium stations in New Zealand using Berkeley Earth adjusted data.

This is even more evident if we look at the 1-year and 5-year moving averages (see Fig. 8.3 above). But if we look at the real data in Fig. 8.1 and plot the 1-year and 5-year moving averages (see Fig. 8.4 below) we again get a different trend entirely from that in Fig. 8.3.

Fig. 8.4: Smoothed warming trends of for long and medium stations in New Zealand using original data.

The question is, why are the data in Fig. 8.3 and Fig. 8.5 so different? The answer is breakpoint alignment.

Fig. 8.5: Difference (Berkeley Earth adjusted data - original data) in the smoothed warming trends for long and medium stations in New Zealand.

If we subtract the data in Fig. 8.4 from that in Fig. 8.3 we get the curves in Fig. 8.5 above. This data is the result of corrections that have been imparted into the data by Berkeley Earth, via a technique called breakpoint alignment or breakpoint adjustment, supposedly to correct for systematic data errors, such as those described above: station moves, changes in instruments and changes to the time of day of measurement. These adjustment are in effect attempting to identify systematic errors between temperature records or within temperature records, and compensate for them.

Yet these changes by Berkeley Earth are clearly not neutral. They do not merely iron out undulations in order to reveal the trend more clearly, they actually add to the trend. In this case these adjustments add 0.33 °C per century to the overall trend. That is more than the original trend in Fig. 8.1, and is why the gradient of the Berkeley Earth best fit line in Fig. 8.3 and Fig. 8.4 is more than double that for the original data in Fig. 8.1 and Fig. 8.4. This is why there is so much scepticism about global warming. Many people outside the climate science community do not trust the data or the analysis. And this is not just a problem with Berkeley Earth. All the major groups do it; it is just that Berkeley Earth are more transparent about it.

What the analysis here has shown is that having more data for recent epochs does not really improve the quality of data in the overall trend, or the confidence level of the conclusions that can be derived from that data. It is more important to have ten long temperature records than twenty (or even a hundred) short ones. Yet herein lies a paradox. The longer the temperature record, the less its quality is trusted by the climate scientists, and the more they seek to fragment if into shorter records via the use of breakpoints. We will see this more clearly later when I look in more detail at the Horlicks that is breakpoint alignment.

 

Addendum

Close inspection of Fig. 8.1 suggests that the spread of the data is greater before 1940 than it is thereafter. This is a consequence of the increased number of datasets that are used to calculate the trend in the latter half of the 20th century compared to the first half and the 19th century. The number of datasets involved in constructing the average temperature trend shown in Fig. 8.1 is indicated below in Fig. 8.6.

 

Fig. 8.6: The number of sets of station data included each month in the temperature trend for New Zealand.

In summary, there were between 5 and 11 datasets used to calculate the trend between 1870 and 1940, and up to 25 thereafter. Given that the standard deviation of the anomalies in most individual temperature records is approximately 1.0 °C, this implies that the standard deviation of the monthly data in the temperature trend should be about 60% greater before 1940 compared to 1980 and later. It also means the uncertainty in the mean trend will increase slightly as you go back in time, from about ±0.2 °C after 1980, to about ±0.35 °C before 1940. Nevertheless, in my view, this indicates that the temperature trend from 1860-1940 is almost as reliable as that for much later years (1960-2010) despite the reduced amount of data. For while the uncertainty before 1940 may be almost double its post 1960 value, it is still significantly less than the natural variation seen in the 5-year moving average temperature.

7. New Zealand - trend due to long stations SLIGHT WARMING

As I pointed out last time, New Zealand has some very good temperature data, or at least good in comparison to most other countries in the Southern Hemisphere. It has over 50 sets of station data, of which ten have over 1200 months of data, and about a dozen have more than 400 months of data, yet even that is not enough.

The stations with over 1200 months of data I shall denote as long stations, those with over 400 months I denote as medium stations. Their geographical locations are shown in Fig. 6.1 in the last post. To start with I shall analyse the long station records, (a) because there are a large number of them, and (b) because they are the records that will show the most discernible trend, yet even with many of these stations the trend can be ambiguous.

If we start with the individual stations, a typical temperature anomaly, i.e. the mean temperature each month minus the monthly reference temperature (MRT), is shown below together with its best fit line and a 5-year moving average. This is the data for Auckland (Albert Park). It dates back to 1853 and it is one of the oldest, longest and most complete records in New Zealand.

Fig. 7.1: Temperature anomaly for Albert Park, Auckland (1853-2013). The best fit line has a positive gradient of 0.18 ± 0.05 °C per century.

Two things are immediately apparent. The first is that the noise level on the anomaly data makes it difficult to discern the overall trend in the data even though the seasonal variation (the MRT) has been removed, and remember, the data represents the average temperature over a whole month not just a typical day. In fact the standard deviation of the data in Fig. 7.1 is 0.95 °C and still almost 25% of data lie outside this range.

The second is that, while the trend does become more discernible if a 5-year moving average is performed (the yellow curve), the trend is still not uniform, nor does it represent a single continuous rise or fall. In fact the temperature in 2013 appears to be no higher than in the 1850s and there is a clear sign of a longer term (150 year) oscillation.

Also shown in Fig. 7.1 is the best fit to the anomaly data. While this fit line has a positive slope of 0.18±0.05 °C per century it needs to be acknowledged that this is not due to a warming trend, but is purely as a consequence of the 150 year oscillation. If you look back at Fig. 4.7 you will recall that the best fit to a full sine wave always has a positive slope. What is clear, however, is that the trend shown in Fig. 7.1 bears no resemblance to the one expected for the region, as illustrated below and on the Berkeley Earth site, either in shape or magnitude.

Fig. 7.2: Berkeley Earth warming trend for New Zealand (1853-2013).

So what about the other nine stations? Well the next three longest are shown in Fig. 7.3. These are the records from Dunedin (ID 18603), Christchurch (157045) and Wellington (18625).

Fig. 7.3: Smoothed temperature anomalies and best fit lines for three stations.

Here the results are even more contradictory. In Fig. 7.3 each set of data is plotted as in the form of the 5-year moving average together with the best fit line. The legend on the graph indicates the slope of each best fit line in degrees Celsius per century, therefore the data for Dunedin-Musselburgh (Berkeley Earth ID = 18603) has a warming trend of 0.64°C per century, while that for Wellington-Kelburn (Berkeley Earth ID = 18625) has a cooling trend of -0.25 °C per century. That for Christchurch (Berkeley Earth ID = 157045) is slightly warming. Of the three datasets, those for Dunedin and Christchurch do appear to offer a passing resemblance to the Berkeley Earth trend in Fig. 7.2, although neither exhibits a temperature gradient as high as that in Fig. 7.2, while Christchurch and Wellington both appear to have a 150 year oscillation that is responsible for most of the slope in the best fit.

Fig. 7.4: Smoothed temperature anomalies and best fit lines for three stations.

If we consider the three next longest records we observe a common theme (see Fig. 7.4). After 1920 there is a distinct warming trend (as was seen in most of the previous data above) but before 1920 much of the important data is missing. Given what we have seen in previous data, it is reasonable to suppose that this data would be of a higher temperature than that which is present, and therefore that the warming trends indicated by the best fit lines in Fig. 7.4 are over-estimates.

Fig. 7.5: Smoothed temperature anomalies and best fit lines for three stations.

For the remaining stations the lack of early data becomes an even bigger problem (see Fig. 7.5), and while a trend post-1940 can be discerned, the early data is highly fragmented. Nevertheless, the last two datasets in Fig. 7.5 both have a peak at about 1890 which is clearly evident on all the data in Fig. 7.1 and Fig. 7.3, and which is at a comparable height relative to the data around 1960 in each case. That suggests that most of this data is consistent and sound.

As I pointed out in post 5, if we wish to derive a regional trend such as that shown in Fig. 7.2, all we need to do is average the anomalies (provided all the data has been processed in a consistent manner and is reliable). When we do this for the ten stations described above, we get the dataset illustrated below in Fig. 7.6.

Fig. 7.6: The warming trend for New Zealand (1853-2013) based on the averaging of long station anomalies. The best fit line has a positive gradient of 0.29 ± 0.04 °C per century.

The mean temperature change or anomaly plotted in Fig. 7.6 has a slight upward trend and its best fit line has a gradient of 0.29±0.04 °C per century. However, this variation is clearly in two parts. From 1860 to 1940 the trend is clearly downwards, while from 1940 to 2000 it is upwards.

What is also clear is that the temperature trends in Fig. 7.6 are very similar to those shown for Auckland in Fig. 7.1 (and actually most of the other individual station datasets) but very dissimilar to that advanced by Berkeley Earth in Fig. 7.2. The question is why?

Well, there are two reasons, and they are both to do with how the temperature data is handled and processed. The graphs I have presented here in Fig. 7.1 and Figs. 7.3-7.6 all use the original temperature data as is. I first calculate the MRT following the method outlined here and subtract it from the original data to obtain the anomaly without the problem of the large seasonal variations. That is a standard procedure that all climate science groups should do. The time base I used for the calculation of the MRT was 1961-1990 for reasons outlined here. Again, this time frame appears to be fairly standard. However, despite this my MRT values differ slightly from those of Berkeley Earth. The reason for this I have not discovered yet, but it may be that old favourite of climate scientists, homogenization, or it may be a different choice of time frame. Whatever the reason, fortunately it makes little difference. If you sum the Berkeley Earth anomalies the result is very similar as shown in below in Fig. 7.7.

Fig. 7.7: The warming trend for New Zealand (1853-2013) based on the averaging of the Berkeley Earth anomalies for long stations.

That, however, is where the similarity ends because Berkeley Earth then play their joker: breakpoint alignment. This is a mathematical device that is supposed to account for imperfections in the data due to human measurement error, changes in instruments, location moves and changes in the time of day when the measurements were made. How this is implemented I will discuss at a later date. What is important here is the net result and that is shown in Fig. 7.8.

Fig. 7.8: The warming trend for New Zealand (1853-2013) based on the averaging of the adjusted Berkeley Earth anomalies for long stations after breakpoint alignment.

The differences between Fig. 7.6 (or Fig. 7.7) and Fig. 7.8 are subtle but clear when you finally see it. In Fig. 7.6 there is a discontinuity or kink in the gradient of the general trend around 1940 and the slope is shallow. In Fig. 7.8 the slope is more uniform and steeper. The gradient of the best fit line has now more than doubled to 0.60 ± 0.04 °C per century and the temperature rise from 1860 to 2010 has gone from virtually zero in Fig. 7.6 to an impressive 0.9 °C. Now, if we smooth the data in Fig. 7.8 using a 12-month and a 10-year moving average, we get the curves shown in Fig. 7.9 below which look very similar to the Berkeley Earth summary trend in Fig. 7.2.

Fig. 7.9: The smoothed warming trend for New Zealand (1853-2013) based on the averaging of the adjusted Berkeley Earth anomalies for long stations after breakpoint alignment.

This validates our averaging process, but the problem is that Fig. 7.9 bears very little resemblance to the original data in Fig. 7.6. This difference cannot be due to a difference in the averaging process, otherwise Fig. 7.9 would not resemble Fig. 7.2 so closely. That only leaves homogenization and breakpoint adjustments as the possible causes of the difference. The equally worrying question is, why are these adjustments being made? Those reasons may become apparent as we look at more of the global temperature data.

6. New Zealand station profile

New Zealand is probably most famous for two things: sheep and rugby (not necessarily in that order). I’m not sure what impact rugby has had on global warming, but sheep are are not exactly carbon-neutral. I shall leave further discussion regarding the methane problem until another day though.

New Zealand is, however, surprising in one sense: despite being a small country with an even smaller population, it has the second highest number of long temperature records in the Southern Hemisphere. Only Australia has more station records with more than 1200 monthly measurements each (1200 being the equivalent of more than 100 years of data). New Zealand therefore seems like a good place to start analysing regional temperature trends.

According to Berkeley Earth, New Zealand has about 64 station records (it may be slightly more or less depending on whether you include some near to Antartica or some South Pacific Islands). Of these, ten have more than 1200 months of temperature data stretching back to the 19th Century, including two that date back to January 1853. I shall characterize these as long stations due to the length of their records. In addition there are a further 27 stations with more than 240 months of data which could be characterized as medium length stations. This includes a further dozen or so stations that contain data covering most of the period from 1973 to 2013.

In my previous post I explained how temperature data can be processed into a usable form comprising the temperature anomaly, and how these anomalies can be combined to produce a global warming trend for the region (see Eq. 5.11 here). This process involves combining multiple temperature records from the same country or region into a single numerical series by adding the anomaly data from the same month in each record and taking the average. This new average should, in theory, have less noise that the individual records from which it is constructed because the averaging process should lead to a regression towards the mean. What is left should be a general trend curve that consists of the signal of long-term climate change for that region together with a depreciated noise component. As a starting point we shall in the next post look at combining the ten longest data sets for New Zealand and seeing how the warming trend it produces compares with the trend as advertised by climate scientists.

As I noted last time, we need to be careful in regard to how the different records are combined, and in particular, to consider two main issues. The first is the evenness of the distribution of the stations across the region in question. If stations are too close together they will merely reproduce each other’s data and render one or more of them redundant. Ideally they should be evenly spaced, otherwise they should be weighted by area (see Eq. 5.15 here).

Fig. 6.1: Geographical distribution of long (1200+ months), medium (400+ months) and short (240+ months) temperature records in New Zealand.

If we look at the spatial distribution of the long stations in New Zealand (see Fig. 6.1.), we see that they are indeed distributed very evenly across the country. This means that weighting coefficients are unnecessary and the local warming trend can be approximated to high precision merely by adding the anomalies from each station record.

The second issue regards the construction of the temperature anomalies themselves (how these anomalies are derived has been discussed here). These anomalies are the amount by which the average temperature for a particular month in a given year has deviated from the expected long-term value for that month. In other words, by how much does the average temperature for this month (May 2020) differ from the average temperature for all months of May over the last 30 years or so? Central to this derivation is the construction of a set of monthly average temperatures, which involves finding the mean temperature for each of the 12 months over a pre-defining time interval of about 30 years as outlined here and in Fig. 4.2 here. I call these averages the monthly reference temperatures (MRTs) because they are temperatures against which the actual data is compared in order to determine the monthly change in temperature. These temperature changes or anomalies are in essence a series of random fluctuations about the mean value, but they may also exhibit an underlying trend over time. It is this trend that climate scientists are seeking to identify and measure.

This immediately raises an important question: over what period should the reference temperature for each month be measured? Most climate science groups seem to favour a thirty year period from 1961-1990. It appears that this is chosen because it tends to correspond to a period with a high number of active stations, and this is certainly true for New Zealand. As the Berkeley Earth graph in Fig. 6.2 below shows, the number of active stations in New Zealand has risen over time, peaking at over 30 in the last few decades. However, when it comes to finding the optimum period for the MRT calculation, relying on station population frequencies is not always the best illustrator.

 Fig. 6.2: New Zealand stations used in the Berkeley Earth average.

What we really require is a time period which allows us to incorporate the maximum number of data points into our analysis. This can be achieved, not by summing the number of active stations each month, but instead by summing the total number of data points that each of the stations present in that month possesses. Such a graph of the sum of station frequency x data length versus time is shown below in Fig. 6.3.

Fig. 6.3: Data frequency over time.

Fig. 6.3 shows more clearly that the period 1970-2000 is the Goldilocks zone for calculating the MRT. Choosing this time period for the MRT not only allows us to incorporate a large number of stations, but it also means we will have a large number of data points per temperature record, and hence a longer trend.  Nevertheless, not all temperature records will have enough data in this region, and some useful data could still be lost. So why not choose a different period, say 10 years, or a longer period, say 50 years or 100 years that could access the lost data? And how much effect would this choice make on the overall warming trend?

The problem is that there are various competing drivers at play here. One is the need to have the longest temperature record, as that will yield the most detectable temperature trend. But measurement accuracy also depends on having the highest number of stations in the calculation, and in having an accurate determination of the MRT for each. And of course, ideally the same time-frame should be used for all the different temperature records that are to be combined in order to maintain data consistency and accuracy. Unfortunately, this is not always possible as most temperature records tend to have different time-frames. When faced with the need to compromise, it is generally best to try different options and seek the optimal one.

5. Combining temperature records into local trends

To see how temperature records can be added or combined it is first necessary to identify the separate components that go to comprise each record.

If we define the temperature record at a position r_i (where i just denotes a label for that location or weather station) on the Earth's surface at time t to be T_i(r_i,t), then each temperature record T_i(r_i,t) can be thought of as the sum of four distinct components as shown below.

 (5.1)

The first of the terms to the right of the equality is the one we are interested in: G(t). This is the global warming trend for the whole planet. It is in effect two terms in one. The first is the benchmark term G(0), which is the global temperature before the start of our measurement, T_i(r_i,t). The second is the change in G(t) over time which we can denote as ∆G(t). So

 (5.2)

The other terms after G(t) in Eq. (5.1) are (in order), the local warming trend (L_i), the seasonal temperature change (S_i), and the local random variations (W_i). These last three terms all vary with time (t) and the location (r_i). The term L_i(r_i,t), like G(t), is actually the sum of two terms, one that denotes the value of L_i(r_i,t) at the start of the temperature record, L_i(r_i,0), and a second that represents the change of L_i(r_i,t) with time, ∆L_i(r_i,t).

  L_i(r_i,t)  =  L_i(r_i,0)  +   ∆L_i(r_i,t).

(5.3)

The term W_i(r_i,t) is just the local weather. It is therefore random and should average to zero, either over time via a temporal moving average on the dataset, T_i(r_i,t), or over position if we combine records from different stations across the globe.

The term S_i(r_i,t) is related to the monthly reference temperature (MRT) that was discussed in the previous post, which we can denote as M_i(r_i,t). So we know how to calculate this, by adding a sufficient amount of data from the same month but different years, in the same record and over multiple years, and finding the mean. However this value will inevitably contain the benchmark values of G(t) and L_i(r_i,t), namely G(0) and L_i(r_i,0) respectively.

(5.4)

Given that T_i(r_i,t) is our data and ∆G(t) or G(t) is what we are trying to measure, the task then is to be able to identify and remove the other three terms L_i , S_i and W_i. We can do this as follows.

The term L_i(r_i,t) is the local warming trend. This is how much the local temperature data is changing with time in a manner that is different from G(t). This could be due to differences in latitude, altitude or local geography (such as whether the station is inland or close to the sea, or surrounded by mountains). However, what is also true of L_i(r_i,t) is that, in absence of any global warming G(t), it should average to a fixed value. But that fixed value would just in effect be a second global warming term that should by rights be part of G(t). In which case it would be logical for the sum of all the local warming terms to equate to zero.

(5.5)

But as already mentioned, the same should be true for the weather component as well:

(5.6)

These two constraints allow us to find the global warming term G(t). To do so we first need to find the temperature anomaly for station or location i.

(5.7)

This, as explained in the last post, is just the difference between the station temperature, T_i(r_i,t), and the MRT. If we substitute for T_i(r_i,t) and M_i(r_i,t) in Eq. 5.7 from the expressions in Eq. 5.1 and 5.4 respectively, together with Eq. 5.2 and Eq. 5.3, after cancellation of terms we get the expression

(5.8)

Now when we sum the anomalies we get

(5.9)

But we know that the summation over W_i(r_i,t) will tend to zero as the number of stations increases, or if a smoothing process is utilised, as will the summation over ∆L_i(r_i,t). So the net result is that if we sum over all possible stations, then

(5.10)

where N is the total number of stations in the summation. Hence the global warming trend is just the mean of the temperature anomalies.

(5.11)

or

(5.12)

If we just sum over all local stations within a region R we will get a similar result, but one that includes the regional trend ∆L_R(t).

(5.13)

As the number of regions in the summation increases, the ∆L_R(t) term will tend to zero and the result will tend to that in Eq. 5.11. It is important to note, however, that when combining anomalies, those anomalies should be derived using MRTs calculated over the same time period. Typically this is chosen to be from 1961 to 1990, mainly because this period contains data from the largest number of temperature records. A second consideration, though, when choosing a suitable period is to select the one where the temperature is most stable. However, given that most temperature records are fairly recent and recent temperature anomalies tend to show the largest rate of warming, it follows that these two criteria are often mutually exclusive. 

What the above analysis demonstrates is that the global warming trend, either globally or locally, is just the sum of the temperature anomalies. None of this requires the climate scientist to determine the local climatic warming L_i(r_i,t). That is just an additional layer of complexity via which the data may possibly be corrupted or even cynically distorted.

The major caveat that one should apply to the above analysis is that it assumes that all stations are equally important in the summation in Eq. 5.13 or Eq. 5.11. This is generally not true as each station effectively represents the area between itself and its nearest neighbours. Hence stations that are more isolated are, therefore, responsible for a larger surface area and should command a stronger weighting.

To account for this we can give each station a weighting coefficient a_i that reflects the proportion of the land area (A_i) that surrounds station i, in comparison to the total land area A_tot. Thus if

(5.14)

then

(5.15)

It is also worth noting the because the areas A_i sum to A_tot, it follows that the coefficients a_i must sum to unity.

So are these weighting coefficients an important consideration? Well most of the major climate science groups that have derived curves for the global warming (NOAA, NASA-GISS, Berkeley Earth and UK Met. Office Hadley Centre/UEA CRU) seem to calculate the area around each station to great precision and use this in the weighting. Personally I think this is generally a waste of effort. I would argue that in most countries the weather stations appear to be fairly uniformly distributed and any variation is relatively small compared to the much larger measurement uncertainties seen in the temperature data. However, there are certainly enormous differences in station densities between countries and also regions (as noted previously), so it is mainly when combining results from different countries and regions that this becomes a major issue, in my opinion.

The main point, however, is this: To get the global warming trend, you just need to average the anomalies. If you do this for a country or a region, the trend will be unique for that country or region. But this will also show you which countries and regions have the greatest warming.

4. Data analysis at the South Pole

If there is one place on Earth that is synonymous with global warming, it is Antarctica. The conventional narrative is that because of climate change, the polar ice caps are melting, all the polar bears and penguins are being rendered homeless and are likely to drown, and the rest of the planet will succumb to a flood of biblical proportions that will turn most of the Pacific islands into the Lost City of Atlantis, and generally lead to global apocalypse. Needless to say, most of this is a gross exaggeration.

I have already explained that melting sea ice at the North Pole cannot raise sea levels because of Archimedes’ principle. The same is true of ice shelves around Antarctica. The only ice that can melt and raise sea levels is that which is on land. In Antarctica (and Greenland) this is virtually all at altitude (above 1000 m) where the mean temperature is below -20 °C, and the mean monthly temperature NEVER gets above zero, even in summer. Consequently, the likelihood of any of this ice melting is negligible.

The problem with analysing climate change in Antarctica is that there is very little data. If you exclude the coastal regions and only look at the interior, there are only twenty sets of temperature data with more than 120 months of data, and only four extend back beyond 1985. Of those four, one has 140 data points and only runs between 1972 and 1986 and so is nigh on useless for our purposes. The other three I shall consider here in detail.

The record that is the longest (in terms of data points), most complete and most reliable is the one that is actually at the South Pole. It is at the Amundsen-Scott Base that is run by the US government and has been permanently manned since 1957. The graph below (Fig. 4.1) illustrates the mean monthly temperatures since 1957.

Fig. 4.1: The measured monthly temperatures at Amundsen-Scott Base.

The thing that strikes you first about the data is the large range of temperatures, an almost 40 degree swing from the warmest months to the coldest. This is mainly due to the seasonal variation between summer and winter. Unfortunately, this seasonal variation makes it virtually impossible to detect a discernible trend in the underlying data. This is a problem that is true for most temperature records, but is acutely so here. However, there is a solution. If we calculate the mean temperature for each of the twelve months individually, and then subtract these monthly means from all the respective monthly temperatures in the original record, what will be left will be a signal representing time dependent changes in the local climate.

Fig. 4.2: The monthly reference temperatures (MRTs) for Amundsen-Scott Base.

The graph above (Fig. 4.2) illustrates the monthly means for the data in Fig. 4.1. We get this repeating data set by adding together all the January data in Fig. 4.1 and dividing it by the number of January readings (i.e. 57). Then we repeat the method for the remaining 11 months. Then we plot the twelve values for each year to give a repeating trend as illustrated in Fig. 4.2. If we then subtract this data from the data in Fig. 4.1 we get the data shown below (Fig. 4.3). This is the temperature anomaly for each month, namely the amount by which the average temperature for that month has deviated from the expected long-term value shown in Fig. 4.2. This is the temperature data that climate scientists are interested in and try to analyse. The monthly means in Fig. 4.2 therefore represent a series of monthly reference temperatures (MRTs) that are subtracted to the raw data in order to generate the temperature anomaly data. The temperature anomalies are therefore the amount by which the actual temperature each month changes relative to the reference or average for that month.

Fig. 4.3: The monthly temperature anomalies for Amundsen-Scott Base.

Also shown in Fig. 4.3 is the line of best fit to the temperature anomaly (red line). This is almost perfectly flat, although its slope is slightly negative (-0.003 °C/century). Even though the error in the gradient is ±0.6 °C per century, we can still venture, based on this data that there is no global warming at the South Pole.

The reasons for the error in the best fit gradient being so large (it is comparable to the global trend claimed by the IPCC and climate scientists) are the large temperature anomaly (standard deviation = ±2.4 °C) and the relatively short time baseline of 57 years (1957-2013). This is why long time series are essential, but unfortunately these are also very rare.

Then there is another problem: outliers. Occasionally the data is bad or untrustworthy. This is often manifested as a data-point that is not only not following the trend of the other data, it is not even in the same ballpark. This can be seen in the data below (Fig. 4.4) for the Vostok station that is located over 1280 km from the South Pole.

Fig. 4.4: The measured monthly temperatures at Vostok.

There is clearly an extreme value for the January 1984 reading. There are also others, including at March 1985 and March 1997, but these are obscured by the large spread of the data. They only become apparent when the anomaly is calculated, but we can remove these data points in order to make the data more robust. To do this the following process was performed.

First, find the monthly reference temperaturs (MRTs) and the anomalies as before. Then, calculate the mean anomaly. Next, calculate either the standard deviation of the anomalies, or the mean deviation (either will do). Then I set a limit for the maximum number of multiples of the deviation that an anomaly data point can lie above or below the mean value for it to be considered a good data point (I generally choose a factor of 5). Any data-points that fall outside this limit are then excluded. Then, with this modified dataset, I recalculated the MRTs and the anomalies once more. The result of this process for Vostok is shown below together with the best fit line (red line) to the resulting anomaly data (Fig. 4.5).

Fig. 4.5: The monthly temperature anomalies for Vostok.

Notice how the best fit line is now sloping up slightly, indicating a warming trend. The gradient, although looking very shallow, is still an impressive +1.00 ± 0.63 °C/century, which is more than that claimed globally by the IPCC for the entire planet. This shows how difficult these measurements are, and how statistically unreliable. Also, look at the uncertainty or error of ±0.63 °C/century. This is almost as much as the measured value. Why? Well, partly because of the short time baseline and high noise level as discussed previously, and partly because of the underlying oscillations in the data which appear to have a periodicity of about 15 years. The impact of these oscillations becomes apparent when we reduce or change the length of the base timeline.

Fig. 4.6: The monthly temperature anomalies for Vostok with reduced fitting range.

In Fig. 4.6 the same data is presented, but the best fit line has only been performed to data between 1960 and 2000. The result is that the best fit trend line (red line) changes sign and now demonstrates long-term cooling of -0.53 ± 1.00 °C/century. Not only has the trend changed sign, but the uncertainty has increased.

What this shows is the difficulty of doing a least squares best fit to an oscillatory dataset. Many people assume that the best fit line for a sine wave lies along the x-axis because there are equal numbers of points above and below the best fit line. But this is not so, as the graph below illustrates.

 Fig. 4.7: The best fit to a sine wave.

The best fit line to a single sine wave oscillation of width 2π and amplitude A is 3A/π² (see Fig. 4.7). This reduces by a factor n for n complete oscillations but it never goes to zero. Only a best fit to a cosine wave will have zero gradient because it is symmetric. Yet the problem with temperature data is that most station records contain an oscillatory component that distorts the overall trend in the manner described above. This is certainly a problem for many of the fits to shorter data sets (less than 20 years). But a far bigger problem is that most temperature records are fragmented and incomplete, as the next example will illustrate.

Fig. 4.8: The measured monthly temperatures at Byrd Station.

Byrd Station is located 1110 km from the South Pole. Its local climate is slightly warmer than those at Amundsen-Scott and Vostok but the variation in seasonal temperature is just as extreme (see Fig. 4.8 above). Unfortunately, its data is far from complete. This means that its best fit line is severely compromised.

Fig. 4.9: The monthly temperature anomalies for Byrd Station.

The best fit to the Byrd Station data has a warming trend of +3.96 ± 0.83 °C/century (see the red line in Fig. 4.9 above). However, things are not quite that simple, particularly given the missing data between 1970 and 1980 which may well consist of a data peak, as well as the sparse data between 2000 and 2010 which appears to coincide with a trough. It therefore seems likely that the gradient would be very different, and much lower, if all data were present. How much lower we will never know. Nor can we know for certain why so much data is missing. Is this because the site of the weather station changed? In which case, can we really consider all the data to being part of a single record, or should we be analysing the fragments separately? This is a major and very controversial topic in climate science. As I will show later, it leads to the development of controversial numerical methods such as breakpoint alignment and homogenization.

What this post has illustrated I hope, is the difficulty of discerning an unambiguous warming (or cooling) trend in a temperature record. This is compounded by factors such as inadequate record length, high noise levels in signals, missing and fragmented data, and underlying nonlinear trends of unknown origin. However, if we can combine records, could that improve the situation? And if we do, would it yield something similar to the legendary hockey stick graph that is so iconic and controversial in climate science? Next I will use the temperature data from New Zealand to try and do just that.