13. The Earth's energy budget

In order to understand how the Earth is heating up, you need to understand why it is warm in the first place. That means you need to know where the energy is coming from and where it is going. That is the basis of the Earth's energy budget or energy balance.

The purpose of this post is to analyse that energy balance, and to determine which parts of it can change, and what the effects of those changes are likely to be. Specifically, this post will try to relate various possible changes in the energy balance to any consequential changes in global temperatures. In so doing, it will also be necessary to critically ascertain the degree of confidence that there is surrounding the various estimates, and measurements, regarding the energy flows in the different parts of the atmosphere.

As I pointed out in the last post, virtually all the energy that is present on Earth originated in the Sun. The amount of energy per second arriving from the Sun at the top of the Earth’s atmosphere is 1361 watts per square metre (W/m²), and as I also pointed out, because the area this energy is ultimately required to heat up (4πr² where r is the Earth's radius) is four times the cross-sectional area that actually captures the energy (πr²), that means that the mean power density (remember: power is rate of flow of energy) that the Earth receives is only a quarter of the incoming 1361 W/m², or about 341 W/m². However as I also showed in Fig. 12.1, not all this energy reaches the Earth's surface. In fact only about 161 W/m² does. The rest is either absorbed by the atmosphere (78 W/m²), reflected by the atmosphere and clouds (79 W/m²), or is reflected by the Earth's surface (23 W/m²). This is shown diagrammatically in Fig. 13.1 below.

  

Fig. 13.1: The Earth's energy budget as postulated by Trenberth et al. (2009).

The image in Fig. 13.1 is taken from a 2009 paper by Kevin Trenberth, John Fasullo and Jeffrey Kiehl (Bull. Amer. Meteor. Soc. 90 (3): 311–324). It is not necessarily the most definitive representation of the energy flows (as we shall see there are other models and significant disparaties and uncertainties in the numbers), but it is probably the most cited. The data it quotes specifically relates to the energy budget for the period March 2000 - May 2004.

Fig. 13.2: The Earth's energy budget as postulated by Kiehl and Trenberth (1997).

The 2009 Trenberth paper is not the first or last paper he has produced on the subject. The energy budget it describes is actually a revision of an earlier attempt from 1997 (J. T. Kiehl and K. E. Trenberth, Bull. Amer. Meteor. Soc., 78, 197–208) shown in Fig 13.2 above, and has since been revised again in 2012 (K. E. Trenberth and J. T.  Fasullo, Surv. Geophys. 33, 413–426) as shown in Fig. 13.3 below.

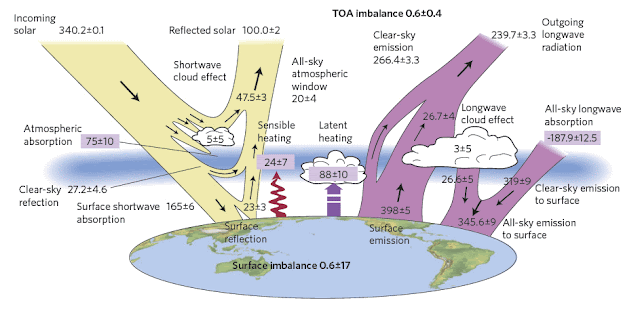
Fig. 13.3: The Earth's energy budget as postulated by Trenberth and Fasullo (2012).

The only real difference between the energy budget in Fig. 13.3 and that from 2009 in Fig. 13.1 is the magnitude of the atmospheric window for long wave infra-red radiation (revised down from 40 W/m² to 22 W/m²), but I still think this highlights the level of uncertainty that there is regarding these numbers. This is further emphasised by a contemporary paper from Stephens et al. (Nature Geoscience 5, 691–696 (2012) ) shown below in Fig. 13.4.

Fig. 13.4: The Earth's energy budget as postulated by Graeme L. Stephens et al. (2012).

As the 2009 Trenberth paper appears to be the most cited it is probably best to use this as the basis for the following discussion, but to bear in mind the amount of uncertainty regarding the actual numbers.

In Fig. 13.1 the three most significant numbers are those for the direct surface absorption from the Sun (161 W/m²), the upward surface radiation (396 W/m²), and the long-wave infra-red back radiation due to the Greenhouse Effect (333 W/m²). Of these it is the upward surface radiation (396 W/m²) that determines the temperature but its value is set by the other two.

As I explained in the last post the emission of electromagnetic radiation from a hot object is governed by the Stefan-Boltzmann law as shown below

  

(13.1)

where I(T) is the power density (per unit area) of the emitted radiation, σ = 5.67 x 10^-8 Wm^-2K^-4 is the Stefan-Boltzmann constant, and the term ε is the relative emissivity of the object. The emissivity defines the proportion of the emission from that object at that wavelength compared to a black body at the same temperature, and it varies with wavelength. It is also different for different materials. In the case of planet Earth, it is generally assumed to be very close to unity all over the surface for all emission wavelengths, but this is not always the case.

It is Eq. 13.1 that allows us to determine the surface temperature (T = 289 K) from the upward surface radiation (396 W/m²) or visa versa. It also allows us to calculate the change in upward surface radiation that would result from a given increase in the surface temperature. It turns out that an increase in surface temperature of 1 °C would necessitate the upward surface radiation increasing from 396 W/m² to 401 W/m², in other words a 1.39% increase. A 2 °C increase would require a 2.80% increase in the upward surface radiation.

I also explained in the last post how the total upward surface radiation (I_T) was related to the direct surface absorption from the Sun (I_o) via a feedback factor f which represented the fraction of upward surface radiation that was reflected back via the Greenhouse Effect.

(13.2)

This model assumed that all the energy absorbed by the greenhouse gases came from one source, though, namely surface upward radiation, and was driven by a single input, the surface absorption of solar radiation, I_o. As Fig. 13.1 indicates, this is not the case. This means that Eq. 13.2 will need to be modified.

The aim here is to determine what changes to the energy flows in Fig. 13.1 would result in a particular temperature rise, specifically a rise of 1 °C in the surface temperature. Realistically, there are only three things that could bring about any significant change. The first is a change in the amount of energy coming from the Sun. The second is is a change in the direct absorption of radiation at the surface, I_o. The third is a change in the strength of the Greenhouse Effect, f.


Case 1: Changes to the incoming solar radiation.

This is probably the easiest of the three propositions to analyse. If the incoming solar radiation at the top of the atmosphere were to change by 1.39%, then we would expect virtually all the projected heat flows in Fig. 13.1 to change by the same amount, including the upward surface radiation (from 396 W/m² to 401 W/m²). This is because almost all the scattering mechanisms and absorption processes in Fig. 13.1 are linear and proportional. The two exceptions are likely to be the thermals (17 W/m²) and the evapo-transpiration (80 W/m²), the former of which will be governed more by temperature differences, and the latter by the non-linear Clausius-Clapeyron equation. While changes to these two components are likely to be linear for small changes, they are unlikely to be proportional. However, as the changes to these two components are likely to be fairly small and comparable to other errors, we can probably ignore these deficiencies. So, if the incoming solar radiation (1361 W/m²) were to increase by 1.39% we could see a global temperature rise of 1 °C.

The problem is that there is no evidence to suggest the Sun's solar output has changed by anything like 1.39% over the last 100 years, and no obvious theoretical mechanism to suggest that it could. The only evidence of change is from satellite measurements over the last 40 years or so that suggest an oscillation in solar output with an eleven year period and an amplitude of about 0.05% (see Fig. 13.5 below). This would give a maximum temperature change of about 0.1 °C.

Fig. 13.5: Changes in the Sun's output since 1979 (from NOAA).

The only other known mechanism is the Milankovitch cycle. This can produce temperature oscillations of over 10 °C in magnitude (peak to trough) but is only seen over 120,000 year cycles (see red curve in Fig. 13.6 below). 

Fig. 13.6: Changes to temperature in the southern oceans (red curve) derived from isotope analysis of the Vostok ice core in Antarctica.

These temperature oscillations are mainly due to changes in the Earth's orbit around the Sun (changes to a more elliptical ortbit), or changes in the Earth's angle of inclination or tilt, or an increased precession that then exposes the polar regions to higher levels of solar radiation. Such effects may be responsible for the cycle of ice ages, but cannot be responsible for changes thought to have happened over the last 100 years. As the data in Fig. 13.6 indicates, even the periods of fastest climate change amounted to only a 10 °C increase over 10,000 years, or 0.1 °C per century, and we do not appear to be in one of those warming periods. If anything, the planet should be slowly cooling by about 0.01 °C per century.

The conclusion, therefore, is that global temperatures may fluctuate by 0.1 °C across the decade due to changes in solar output, but there is no evidence or credible mechanism that would support a long-term warming trend.


Case 2: Changes to the direct absorption of radiation at the surface.

The second possible driver of global warming comes from changes at the surface, specifically to the thermal energy absorbed there, I_o. This will then impact on the total upward surface radiation I_T and thereby also on the back radiation. According to Eq. 13.2 the changes to I_o and I_T should be proportional. As Eq. 13.1 indicates that a 1 °C change to the surface temperature, T_o, should result in a 1.39% change to I_T, it follows that a 1.39% change to I_o should result in a 1 °C change to T_o. Unfortunately there are three additional complications that we need to consider: the thermals (I_th = 17 W/m²), the evapo-transpiration (I_E = 80 W/m²), and the incoming solar radiation absorbed by the atmosphere (I_A = 78 W/m²).

The thermals (17 W/m²) and evapo-transpiration (80 W/m²) in Fig. 13.1 transfer heat from the surface into the upper atmosphere (top of the tropopause) by mass transfer (convection) rather than radiation. This may potentially provide a route for heat to escape from the Earth via a by-passing of the greenhouse mechanism. However, I would expect this energy to eventually get dumped in the atmosphere somewhere before the top of the tropopause (at a height of 20 km). When this happens it will merely add to the long-wave infra-red radiation being emitted from the surface, and so should still be reflected by the greenhouse gases. So while these heat sources will not contribute to the surface temperature as defined in Eq. 13.1, they should be included in the feedback factor f in Eq. 13.2.

So too will some of the power absorbed by the atmosphere directly from the incoming solar radiation (78 W/m²). Here again things are complicated because if the energy is absorbed before the bottom of the stratosphere (at 20 km altitude), the Greenhouse Effect will actually reflect some of that heat back into space. To account for this we can include an additional parameter μ as a variable that specifies the proportion of the incoming solar absorbed by the atmosphere that is absorbed in the lower atmosphere where it can be reflected backwards the surface. The fraction (1-μ) absorbed in the upper atmosphere will escape and therefore will not contribute to the back radiation.

In all there are seven energy terms that we need to consider.

1. Initial surface absorption (I_o = 161 W/m²).
2. Thermals (I_th = 17 W/m²).
3. Evapo-transpiration (I_E = 80 W/m²).
4. Upward surface long-wavelength radiation (I_up = 396 W/m²).
5. Long-wavelength back radiation (I_RF = 333 W/m²).
6. Incoming solar absorbed by the atmosphere (I_A = 78 W/m²).
7. Net radiation permanently absorbed by the Earth's surface (I_net = 0.9 W/m²).

We must then consider energy conservation at the surface and in the atmosphere. At the surface the law of conservation of energy (1st law of thermodynamics) requires that

 (13.3)

while in the atmosphere similar considerations mean that the total energy entering the atmosphere must equal the total that is emitted. As f is the proportion that is reflected back it follows that

(13.4)

The parameter μ is a variable that specifies the proportion of the incoming solar absorbed by the atmosphere (I_A) that is absorbed in the lower atmosphere where it can be reflected back towards the surface. The fraction (1-μ) absorbed in the upper atmosphere will escape and therefore will not contribute to I_RF. It therefore follows that

(13.5)

Using Eq. 13.5 we can work out a value for f, but only if we know μ, which we don't. However, using Eq. 13.4 and the knowlege that μ must lie in the range 0 <  μ < 1, we can say that f will be in the range 0.583 to 0.675 and that when μ = 0.5, f = 0.626. This allows us to estimate the change required in I_o to generate a 1 °C change in T_o, but to do that we will need to make some assumptions given the number of variables that there are.

First we can probably assume that f, μ and I_A remain unchanged even when I_o changes. We know that a 1 °C increase in T_o will result in a 1.39% increase in I_up to 401.5 W/m² and a 2 °C increase in T_o will result in a 2.80% increase in I_up to 407.1 W/m². The question is what happens to the thermals (I_th), the evapo-transpiration (I_E) and the net surface absorption (I_net)? They will probably increase as well, but by how much? A good starting point is to assume that they will increase by the same percentage as the upward surface long-wavelength radiation (I_up). A benchmark control is to assume that they stay constant. This gives us the following two scenarios.

If I_th, I_E and I_net scale with I_up and the scaling factor due to the increase in temperature T_o is g, then Eq. 13.5 can be rearranged to give

(13.6)

whereas if I_th, I_E and I_net are constant then

(13.7)

We know that g = 1.0139 for a 1 °C rise in T_o and g = 1.0280 for a 2 °C rise in T_o. So combining the two options in Eq. 13.56 and Eq. 13.7 implies that I_o is in the range 162.8-163.9 W/m². That implies an excess direct heating at the surface of ∆I_o = 2.33 ± 0.54 W/m², with the error range being set by the range of possible values for f, μ, I_E, I_net and I_th. A 2 °C increase in surface temperature would require a change in direct heating at the surface of ∆I_o = 4.69 ± 1.09 W/m².

The conclusion, therefore, is that a 1 °C increase in global temperatures would require an increase in the initial surface absorption of ∆I_o = 2.3 ± 0.5 W/m². How this might be achieved will be explored further in the next post.


Case 3: Changes to the feedback factor.

The most obvious and heavily reported mechanism by which global temperatures could increase is via changes to the Greenhouse Effect due to increased carbon dioxide concentrations in the atmosphere. The specific change that will ensue will be in the value of the feedback term, f, and hence the value of the back radiation, I_RF. As in the previous case, some of the heat flow parameters in Fig. 13.1 would change and some would stay the same. For example, we can confidently assume that I_A and I_o will remain unchanged, but if f changes, so might μ. But as before, the main question is what happens to the thermals (I_th) and the evapo-transpiration (I_E)?

Rearranging Eq. 13.5 once more gives

 (13.8)

while for the case that I_th, I_E and I_net are constant we get

 (13.9)

It turns out there is very little difference in the results using the two methods. The biggest factor affecting f is the value of μ. When there is no warming (g = 1.0) f = 0.629. A warming of 1 °C (g = 1.0139) requires f to increase to 0.634, and a warming of 2 °C (g = 1.0280) requires f to increase to 0.638. These values all correspond to values for μ of 0.5, but the possible spread of values for μ leads to an error in f of ±0.047 in all cases.

What this shows is that the increase in feedback factor needed for a 1 °C rise in global temperatures will be about 0.005. This is a small change, but at the end of the last post (Post 12) I calculated that the fraction of the long-wave infra-red radiation that could be absorbed and reflected by the carbon dioxide in its main absorption band (the frequency range 620-720 wavenumbers or the wavelength range 13.89 - 16.13 μm). The result was at best 10.5%. This implies that only about 15% of the Greenhouse Effect is due to CO₂, and the rest is due to other agents, mainly water vapour.

The conclusion, therefore, is that a 1 °C increase in global temperatures would require an increase in the width or strength of the carbon dioxide absorption band by at least 5% relative to its current size in order achieve this temperature rise.


The final point to note is the size of the potential measurement errors in the various energy flows, and the effect of rounding errors. A particular egregious anomaly occurs at the top of the atmosphere in Fig. 13.1 (and remains uncorrected in Fig. 13.3) where the rounded value of the incoming solar (341 W/m²) radiation balances the rounded outgoing values (239 W/m² and 102 W/m²). This is inconsistent with the rest of the diagram as there should be a 0.9 W/m² difference to account for the net absorption at the surface. In the more exact values quoted (341.3 W/m², 238.5 W/m² and 101.9 W/m²) this difference is specified correctly. So the problem is a rounding issue initially, but it then has a knock-on effect for the values quoted within the atmosphere.

For consistency it would therefore be better in this instance to round the 238.5 W/m² value down (to 238 W/m²) rather than up (to 239 W/m²). That would ensure that there was a net inflow of about 1 W/m² that balanced the net absorbed value at the surface (0.9 W/m²). It would also eliminate the false imbalance within the atmosphere itself. Here the net inflow should balance the net outflow (currently there is a 1 W/m² deficit). There can be no 0.9 W/m² energy gain in the atmosphere otherwise the atmosphere would heat up, and heat up by more than 2.7 °C per annum. What should remain invariant at various points from the surface to the top of the atmosphere is the following energy balance

(13.10)

where I_TOA = 238.5 W/m² is the outgoing long-wave radiation at the top of the atmosphere. A correction for this error requires the stated value for the power emitted upwards by the atmosphere (169 W/m²) in Fig. 13.1 to be reduced to 168 W/m².

It is also important to note that some of the errors in the energy flows in Fig. 13.1-Fig.13.4 are considerable, either in magnitude, or as a percentage. A comparison of the data in Fig. 13.1 and Fig. 13.4 illustrates how variable the results can be. The back radiation values, for example, do not agree within the noted error range, and the net surface absorption is 50% higher in Trenberth's papers than it is in the Stephens paper (Fig. 13.4). I shall look at the net surface absorption in more detail later as it has important implications for sea level rise, but the fact that this value is so small, not just relative to the other energy flows, but also in comparison to their errors, is a cause for concern with respect to its own accuracy. It should also be noted that the net surface absorption should also be measurable directly at the top of the atmosphere using satellite technology to measure both the solar energy going in and the Earth's thermal energy flowing out. Yet the discrepancies seen there between incoming and outgoing energy flows currently far exceed 0.9 W/m². The result is that most of the energy flows shown in Fig. 13.1-Fig.13.4 are at best estimates, and are often based more on climate models than on actual data.